Đề kiểm tra học kì I (đề số 3)

Câu 1 (1đ):

Cho hàm số $y=f(x)$ có bảng biến thiên như sau:

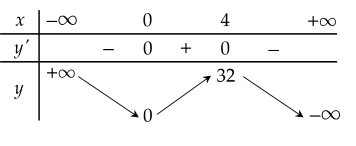
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

(0;4)

.

(-\infty ;0)

.

(3;+\infty)

.

(0;32)

.

Câu 2 (1đ):

Cho hàm số $y=-x^4+2x^2+3$ . Mệnh đề nào dưới đây đúng?

Hàm số có

1

điểm cực đại và

1

điểm cực tiểu.

Hàm số không có cực đại, chỉ có

1

điểm cực tiểu.

Hàm số có

1

điểm cực đại và

2

điểm cực tiểu.

Hàm số có

2

điểm cực đại và

1

điểm cực tiểu.

Câu 3 (1đ):

Cho hàm số $y=f\left( x \right)$ có bảng xét dấu đạo hàm như sau.

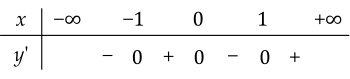
loading...

Mệnh đề nào sau đây đúng?

\underset{\left( -1;\,+\infty \right)}{\mathop{\min }}\,f\left( x \right)=f\left( 0 \right)

.

\underset{\left( 0;\,+\infty \right)}{\mathop{\max}}\,f\left( x \right)=f\left( 1 \right)

.

\underset{\left( -\infty ;\,-1 \right)}{\mathop{\min }}\,f\left( x \right)=f\left( -1 \right)

.

\underset{\left( -1;\,1 \right]}{\mathop{\max}}\,f\left( x \right)=f\left( 0 \right)

.

Câu 4 (1đ):

Số đường tiệm cận của đồ thị hàm số $y=\dfrac{2x-1}{2x+3}$ là

1

.

3

.

2

.

0

.

Câu 5 (1đ):

Cho hàm số $y=-\dfrac{2x^3}{3}+x^2+4x-2$ , gọi đồ thị của hàm số là $(C)$ . Đường thẳng nào sau đây tiếp xúc với đồ thị hàm số $(C)$ ?

y=-\dfrac{3}{4}x-\dfrac{5}{2}

.

y=-\dfrac{3}{4}x-\dfrac{1}{2}

.

y=-\dfrac{3}{4}x+\dfrac{1}{2}

.

y=-\dfrac{3}{4}x-\dfrac{7}{2}

.

Câu 6 (1đ):

Một sinh viên đo độ dài của một số lá dương xỉ trưởng thành, kết quả như sau:

Lớp độ dài (cm)	Tần số
$\big[10 \, ; \, 20\big)$	$8$
$\big[20 \, ; \, 30\big)$	$6$
$\big[30 \, ; \, 40\big)$	$24$
$\big[40 \, ; \, 50\big)$	$10$

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là

35

.

45

.

40

.

30

.

Câu 7 (1đ):

Trong không gian $Oxyz$ , cho hai vectơ $\overrightarrow{a}=(-1 ; 3 ;-3)$ và $\overrightarrow{b}=(2 ; 1 ;-2)$ . Tọa độ của vectơ $\overrightarrow{b}-\overrightarrow{a}$ là

(1 ; 4 ;-5).

(3 ;-2 ; 1).

(1 ;-2 ; 3).

(3 ; 2 ;-1).

Câu 8 (1đ):

Giá trị của $m$ để giá trị nhỏ nhất của hàm số $y=x^3-3mx^2+6$ trên đoạn $[0;3]$ bằng $2$ là

m=1

.

m>\dfrac32

.

m=2

.

m=\dfrac{31}{27}

.

Câu 9 (1đ):

Cho hàm số $y=\dfrac{mx^2+\left(3m^2-2 \right)x-2}{x+3m}$ . Số giá trị của $m$ để góc giữa hai đường tiệm cận của đồ thị hàm số bằng $45^\circ$ là

3

.

4

.

5

.

2

.

Câu 10 (1đ):

Thống kê độ tuổi tập thể dục thể thao hàng ngày trong một cụm dân cư có bảng số liệu sau:

Độ tuổi	Số người
$[10; 20)$	$10$
$[20;30)$	$6$
$[30;40)$	$15$
$[40;50)$	$19$
$[50;60)$	$25$

Phương sai của mẫu số liệu trên (kết quả làm tròn đến hàng phần trăm) là

187,13

.

187,03

.

189,66

.

13, 68

.

Câu 11 (1đ):

Trong không gian với hệ trục tọa độ $Oxyz$ , cho ba điểm $A(1;2;-1)$ , $B(2;-1;3)$ , $C(-2;3;3)$ . Điểm $D( a;\,b;\,c)$ là đỉnh thứ tư của hình bình hành $ABCD$ , khi đó $P=a^2+b^2-c^2$ có giá trị bằng

42

.

45

.

44

.

43

.

Câu 12 (1đ):

Nếu một vật có khối lượng $m$ (kg) thì lực hấp dẫn $\overrightarrow{P}$ (N) của Trái Đất tác dụng lên vật được xác định theo công thức: $\overrightarrow{P}=m . \overrightarrow{g}$ , trong đó $\overrightarrow{g}$ là gia tốc rơi tự do có độ lớn $g=9,8$ m/s $^2$ . Độ lớn của lực hấp dẫn của Trái Đất tác dụng lên một quả cam có khối lượng $250$ gam gần nhất với giá trị nào sau đây?

2,35

N.

2,51

N.

2,54

N.

2,45

N.

Câu 13 (1đ):

Trong không gian $Oxyz$ , cho tam giác $ABC$ có $A(1;\,2;\,4),\,B(4;\,-2;\,1),\,C(3;\,4;\,7)$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Toạ độ trọng tâm $G$ của tam giác $ABC$ là $G\Big( \dfrac{8}{3};\,\dfrac{4}{3};\,4 \Big)$ .
b) Toạ độ điểm $D$ sao cho $ABCD$ là hình bình hành là $D( 0;\,8;\,10)$ .
c) Toạ độ điểm $M$ thuộc đoạn $AB$ sao cho $MB=2MA$ là $M\Big( 2;\,\dfrac{2}{3};\,3 \Big)$ .
d) $\cos \widehat{BAC}=\dfrac{11\sqrt{2}}{34}$ .

Câu 14 (1đ):

Chi phí nhiên liệu của một chiếc tàu chạy trên sông được chia làm hai phần. Phần thứ nhất không phụ thuộc vào vận tốc và bằng $480$ nghìn đồng mỗi giờ. Phần thứ hai tỉ lệ thuận với lập phương của vận tốc, khi $v=10$ km/h thì phần thứ hai bằng 30 nghìn đồng mỗi giờ.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Khi vận tốc $v=10$ (km/h) thì chi phí nguyên liệu cho phần thứ nhất trên mỗi km đường sông là $48\,000$ đồng.
b) Hàm số xác định tổng chi phí nguyên liệu trên mỗi km đường sông với vận tốc $x$ km/h là $f(x)=\dfrac{480}{x}+0,03 x^{3}$ .
c) Khi vận tốc $v=30$ km/h thì tổng chi phí nguyên liệu trên mỗi km đường sông là $43\,000$ đồng.
d) Vận tốc của tàu để tổng chi phí nguyên liệu trên mỗi km đường sông nhỏ nhất là $v=20$ km/h.

Câu 15 (1đ):

Cho hàm số $y=f\left(x \right)$ có bảng biến thiên như hình dưới đây:

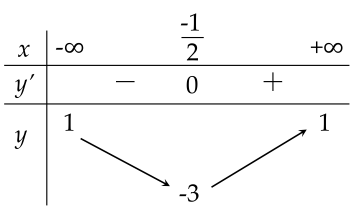
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Hàm số $y=f\left(x \right)$ xác định và liên tục trên $\mathbb{R}$ .
b) Hàm số $y=f\left(x \right)$ có một điểm cực đại.
c) Đồ thi hàm số $y=f\left(x \right)$ có $1$ tiệm cận đứng.
d) Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số $y=\dfrac{1}{2f\left(x \right)-1}$ là $3$ .

Câu 16 (1đ):

Thu nhập theo tháng (đơn vị: triệu đồng) của người lao động ở hai nhà máy như sau:

Thu nhập	Số người của nhà máy A	Số người của nhà máy B
$[5;8)$	$20$	$17$
$[8;11)$	$35$	$23$
$[11;14)$	$45$	$30$
$[14;17)$	$35$	$23$
$[17;17)$	$20$	$17$

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Nhà máy $A$ có số lượng người lao động nhiều hơn nhà máy $B.$
b) Mức thu nhập trung bình của người lao động ở hai nhà máy này bằng nhau.
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm của mẫu số liệu thu nhập của người lao động nhà máy $A$ nằm trong khoảng $(5;5,5)$ .
d) Xét theo khoảng tứ phân vị, ta thấy mức thu nhập của số người nhà máy $A$ phân tán hơn so với mức thu nhập của số người nhà máy $B.$

Câu 17 (1đ):

Bảng thống kê cân nặng của $50$ quả xoài được lựa chọn ngẫu nhiên sau khi thu hoạch ở nông trường như sau:

Cân nặng (g)	Số quả xoài
$[250;290)$	$2$
$[290;330)$	$12$
$[330;370)$	$19$
$[370;410)$	$12$
$[410;450)$	$5$

Tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.

Trả lời: .

Câu 18 (1đ):

Có bao nhiêu giá trị nguyên của tham số $m$ thuộc đoạn $[-20 ; 20]$ để hàm số $y=x^4-2(m-1)x^2+m-2$ đồng biến trên khoảng $(1;3)$ ?

Trả lời:

Câu 19 (1đ):

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật với $SA=4,\,AB=1,\,AD=2$ và $SA\bot \left(ABCD \right)$ . Gọi $M$ là trung điểm của $AB$ . Tính góc giữa hai vectơ $\overrightarrow{SC}$ và $\overrightarrow{DM}$ . (làm tròn đến đơn vị độ)

loading...

Trả lời: $^\circ$

Câu 20 (1đ):

Một sợi dây có chiều dài là $6$ m, được chia thành hai phần. Phần thứ nhất được uốn thành hình tam giác đều, phần thứ hai uốn thành hình vuông. Độ dài của cạnh hình tam giác đều bằng bao nhiêu mét để diện tích hai hình thu được là nhỏ nhất? (kết quả làm tròn đến hàng phần trăm)

loading...

Trả lời:

Câu 21 (1đ):

Có bao nhiêu giá trị nguyên của tham số $m$ để đồ thị hàm số $y=3x+\dfrac{mx}{\sqrt{{{x}^{2}}+3}}$ có các điểm cực trị nằm trong hình tròn tâm $O$ , bán kính $R=\sqrt{130}$ ?

Trả lời:

Câu 22 (1đ):

Cho hàm số $y=f(x)$ có bảng biến thiên như sau:

loading...

Có bao nhiêu giá trị nguyên của tham số $m$ để phương trình $6f\left(x^2-4x \right)=m$ có ít nhất ba nghiệm thực phân biệt thuộc khoảng $\left(0;+\infty \right)$ ?

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra học kì I (đề số 3) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra học kì I (đề số 3) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP