Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra học kì I (đề số 2) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Bảng sau thống kê cân nặng của 30 quả đu đủ được lựa chọn ngẫu nhiên sau khi thu hoạch ở vườn nhà Lan.
| Cân nặng (g) | Số quả bưởi |
| [750;800) | 5 |
| [800;850) | 10 |
| [850;900) | 5 |
| [900;950) | 8 |
| [950;1000) | 2 |
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
Trong không gian Oxyz, biết OM=2i−3j+k. Toạ độ của điểm M là
Phương trình tiếp tuyến của đồ thị hàm số y=x−12x+1 tại điểm có hoành độ x=2 là
Các đường tiệm cận ngang của đồ thị hàm số y=4x2+12x−1 là
Cho hàm số y=3(x2−4)2 có đồ thị như hình vẽ sau.
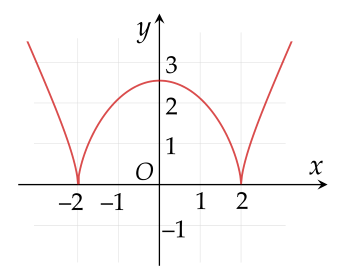
Khoảng nghịch biến của hàm số trên là
Khảo sát thời gian chơi thể thao trong một ngày của 40 học sinh lớp 10A giáo viên thu được một mẫu dữ liệu ghép nhóm như sau:
| Thời gian (phút) | Số học sinh |
| [30;40) | 2 |
| [40;50) | 10 |
| [50;60) | 16 |
| [60;70) | 8 |
| [70;80) | 2 |
| [80;90) | 2 |
Khoảng tứ phân vị của bảng số liệu ghép nhóm trên là
Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC có ba đỉnh A(−1;1;−3), B(4;2;1), C(3;0;5). Tọa độ trọng tâm G của tam giác ABC là
Cho hàm số y=cx+dax+b có đồ thị như sau:
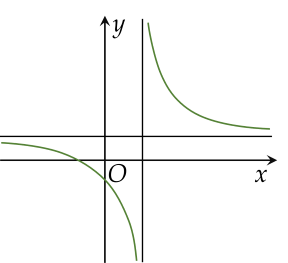
Mệnh đề nào sau đây đúng?
Để loại bỏ x% chất gây ô nhiễm không khí từ khí thải của một nhà máy, người ta ước tính chi phí cần bỏ ra là C(x)=100−x300x (triệu đồng), 0≤x≤100 trong đó C(x) là hàm số xác định trên[0;100]. Đường tiệm cận đứng của đồ thị hàm số y=C(x) là đường thẳng x=x0. Giá trị của x0 là
Giá trị lớn nhất của hàm số y=x4−2x2+3 trên đoạn [0;3] là
Cần phải làm cái cửa sổ mà phía trên là hình bán nguyệt, phía dưới là hình chữ nhật, có chu vi là a (m) (a chính là chu vi hình bán nguyệt cộng với chu vi hình chữ nhật trừ đi độ dài cạnh hình chữ nhật là dây cung của hình bán nguyệt).

Các kích thước (đơ vị mét) của nó để diện tích cửa sổ lớn nhất là
Cho hàm số y=x3−3x2+5 có đồ thị (C). Độ dài đoạn thẳng nối hai điểm cực trị của đồ thị (C) bằng
Cho bảng số liệu ghép nhóm thống kê số thẻ vàng của mỗi câu lạc bộ trong giải ngoại hạng Anh mùa giải 2021 – 2022 cho kết quả sau:
| Số thẻ vàng | Tần số |
| [40;50) | 2 |
| [50;60) | 5 |
| [60;70) | 7 |
| [70;80) | 5 |
| [80;90) | 0 |
| [90;100) | 0 |
| [100;110) | 1 |
| a) Cỡ mẫu của mẫu số liệu trên là 20. |
|
| b) Khoảng biến thiên của mẫu số liệu trên là 50. |
|
| c) Tứ phân vị của thứ nhất của mẫu số liệu gốc thuộc vào nhóm [50;60). |
|
| d) Khoảng tứ phân vị của mẫu số liệu trên là ΔQ=26. |
|
Cho hai vectơ a và b thỏa mãn ∣a∣=2; ∣b∣=5, góc giữa hai vectơ a và b bằng 60∘.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) (a,−2b)=60∘. |
|
| b) a.b=5. |
|
| c) ∣a−2b∣=84. |
|
| d) Biết vectơ v ngược hướng với vectơ a−2b và ∣v∣=421. Gọi α là góc giữa hai vectơ v và a. Khi đó cosα=8421. |
|
Cho hàm số y=x−1x2−2x−3.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Đồ thị hàm số nhận đường thẳng y=x+1 làm tiệm cận xiên. |
|
| b) Hàm số có hai điểm cực trị. |
|
| c) Gọi A,B,C là giao điểm của đồ thị hàm số với các trục Ox,Oy. Diện tích tam giác ABC bằng 6. |
|
| d) Có đúng hai giá trị nguyên của tham số m để hàm số f(x)=x−1x2−2x−3−m2x đồng biến trên từng khoảng xác định. |
|
Sự phân huỷ của rác thải hữu cơ có trong nước sẽ làm tiêu hao oxygen hoà tan trong nước. Nồng độ oxygen (mg/l) trong một hồ nước sau t giờ (t≥0) khi một lượng rác thải hữu cơ bị xả vào hồ được xấp xỉ bởi hàm số y(t)=5−9t2+115t. (có đồ thị như đường màu cam ở hình bên)

| a) Vào thời điểm t=1 thì nồng độ oxygen trong nước là 3,5 mg/l. |
|
| b) Nồng độ oxygen (mg/l) trong một hồ nước không vượt quá 5 mg/l. |
|
| c) Vào thời điểm t=0 thì nồng độ oxygen trong nước cao nhất. |
|
| d) Nồng độ oxygen (mg/l) trong một hồ nước thấp nhất là 3,5 mg/l. |
|
Thành tích môn nhảy cao của các vận động viên tại một giải điền kinh dành cho học sinh trung học phổ thông như sau:
| Mức xà (cm) | Số vận động viên |
| [170;172) | 3 |
| [172;174) | 10 |
| [174;176) | 6 |
| [176;180) | 1 |
Tính độ lệch chuẩn của mẫu số liệu đã cho. (Làm tròn kết quả đến chữ số hàng phần trăm).
Trả lời: .
Cho hình hộp ABCD.A′B′C′D′. Một đường thẳng Δ cắt các đường thẳng AA′,BC,C′D′ lần lượt tại M,N,P sao cho NM=2NP. Tính MA′MA.
Trả lời:
Trong hóa học cấu tạo của phân tử ammoniac (NH3) có dạng hình chóp tam giác đều mà đỉnh là nguyên tử nitrogen (N) và đáy là tam giác H1H2H3 với H1,H2,H3 là vị trí của ba nguyên tử hydrogen (H). Góc tạo bởi liên kết H−N−H, có hai cạnh là hai đoạn thẳng nối N với hai trong ba điểm H1,H2,H3 (chẳng hạn như H1NH2) , được gọi là góc liên kết của phân tử NH3. Góc này xấp xỉ 120∘. Trong không gian Oxyz, cho một phân tử NH3 được biểu diễn bởi hình chóp tam giác đều N.H1H2H3 với O là tâm của đáy. Nguyên tử nitrogen được biểu diễn bởi điểm N thuộc trục Oz, ba nguyên tử hydrogen ở các vị trị H1,H2,H3 trong đó H1(0;−3;0) và H2H3 song song với trục Ox. Tính khoảng cách giữa nguyên tử nitrogen với mỗi nguyên tử hydrogen. (làm tròn kết quả đến hàng phần trăm)
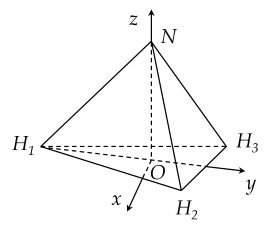
Trả lời:
Cho hàm số y=f(x) liên tục trên R, có đồ thị (C) như hình vẽ sau:
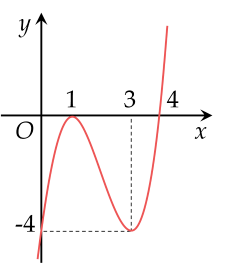
Phương trình ∣f(x)∣=2 có bao nhiêu nghiệm trên đoạn [0;3]?
Trả lời:
Hàm số y=(x+m)3+(x+n)3−x3 đồng biến trên khoảng (−∞;+∞). Giá trị nhỏ nhất của biểu thức P=100[4(m2+n2)−m−n] bằng bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ nhất)
Trả lời:
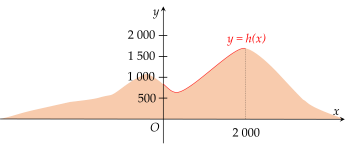
Một phần lát cắt của dãy núi có độ cao tính bằng mét được mô tả bởi hàm số y=h(x)=−13200001x3+35209x2−4481x+840 với 0≤x≤2000. Biết đỉnh của lát cắt dãy núi nằm ở độ cao h (m) thuộc đoạn [1000;2000]. Tính h. (Kết quả làm tròn đến hàng đơn vị)
Trả lời:
