Đề kiểm tra học kì I (đề số 1)

Câu 1 (1đ):

Xét mẫu số liệu ghép nhóm cho bởi bảng sau:

Nhóm	Tần số
$[40;45)$	$4$
$[45;50)$	$11$
$[50;55)$	$9$
$[55;60)$	$8$
$[60;65)$	$8$

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là

25

.

6

.

5

.

40

.

Câu 2 (1đ):

Trong hệ toạ độ $Oxyz$ , cho $\overrightarrow{m}=(2;4;1 )$ và $\overrightarrow{n}=(0;7;6 )$ . Toạ độ của vectơ $\overrightarrow{t}=\overrightarrow{m}-\overrightarrow{n}$ là

\overrightarrow{t}=(-2;3;5 )

.

\overrightarrow{t}=(2;-3;-5)

.

\overrightarrow{t}=(3;-3;-5 )

.

\overrightarrow{t}=(5;-3;-5 )

.

Câu 3 (1đ):

Trong không gian $Oxyz$ , cho các điểm $A(1;2;0 )$ , $B(-1;0;1 )$ , $C(0;2;-1 )$ . Độ dài của vectơ $\overrightarrow{AB}-2\overrightarrow{AC}$ bằng bao nhiêu?

13

.

\sqrt{13}

.

\sqrt{21}

.

21

.

Câu 4 (1đ):

Trong không gian $Oxyz$ , cho điểm $A\left(4;\,-2;\,3 \right)$ . Tọa độ $\overrightarrow{AO}$ là

\left(-2;\,3;\,4 \right)

.

\left(-4;\,2;\,-3 \right)

.

\left(-2;\,4;\,3 \right)

.

\left(4;\,2;\,-3 \right)

.

Câu 5 (1đ):

Hàm số $y=x^3-3x^2$ nghịch biến trên khoảng nào dưới đây?

(2;+\infty)

.

(-\infty ;1)

.

(0;2)

.

(-1;1)

.

Câu 6 (1đ):

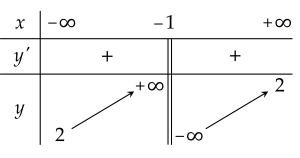
loading...

Hình trên là bảng biến thiên của hàm số nào trong bốn hàm số dưới đây?

y=\dfrac{2x+3}{x+1}

.

y=\dfrac{x-1}{x+1}

.

y=\dfrac{2x-1}{x+1}

.

y=\dfrac{2x-1}{x-1}

.

Câu 7 (1đ):

Cho hàm số $y=f(x )$ liên tục và xác định trên $\mathbb{R}\backslash \{2\}$ có đồ thị là đường cong $(C )$ và các giới hạn $\underset{x\to 2^+}{\mathop{\lim }}\,f(x )=1$ ; $\underset{x\to 2^-}{\mathop{\lim }}\,f(x )=1$ ; $\underset{x\to -\infty }{\mathop{\lim }}\,f(x )=2$ ; $\underset{x\to +\infty }{\mathop{\lim }}\,f(x )=2$ . Khẳng định nào dưới đây đúng?

Đường thẳng

y=1

là tiệm cận ngang của

(C)

.

Đường thẳng

x=2

là tiệm cận ngang của

(C)

.

Đường thẳng

x=2

là tiệm cận đứng của

(C )

.

Đường thẳng

y=2

là tiệm cận ngang của

(C)

.

Câu 8 (1đ):

Cho hàm số $y=f(x)$ có bảng biến thiên như sau:

Khẳng định nào sau đây đúng?

\underset{[-3;2]}{\mathop{\max}} f(x)=3

.

\underset{[-3;2]}{\mathop{\max}} f(x)=-2

.

\underset{[-3;2]}{\mathop{\max}} f(x)=2

.

\underset{[-3;2]}{\mathop{\max}} f(x)=1

.

Câu 9 (1đ):

Giả sử kết quả khảo sát khu vực A về độ tuổi kết hôn của một số phụ nữ vừa lập gia đình được cho ở bảng sau:

Tuổi kết hôn	Tần số	Tần số tích lũy
$[19;22)$	$10$	$10$
$[22;25)$	$27$	$37$
$[25;28)$	$31$	$68$
$[28;31)$	$25$	$93$
$[31;34)$	$7$	$100$

Khoảng tứ phân vị của mẫu số liệu trên là

\Delta_Q=\dfrac{388}{75}

.

\Delta_Q=\dfrac{288}{75}

.

\Delta_Q=\dfrac{386}{75}

.

\Delta_Q=\dfrac{378}{75}

.

Câu 10 (1đ):

Cho hình lăng trụ $A B C . A' B' C', \, M$ là trung điểm của $B B'$ . Đặt $\overrightarrow{C A}=\overrightarrow{a}, \, \overrightarrow{C B}=\overrightarrow{b}, \, \overrightarrow{A A'}=\overrightarrow{c}$ . Khẳng định nào sau đây đúng?

\overrightarrow{A M}=\overrightarrow{a}-\overrightarrow{c}+\dfrac{1}{2} \overrightarrow{b}

.

\overrightarrow{A M}=\overrightarrow{b}-\overrightarrow{a}+\dfrac{1}{2} \overrightarrow{c}

.

\overrightarrow{A M}=\overrightarrow{a}+\overrightarrow{c}-\dfrac{1}{2} \overrightarrow{b}

.

\overrightarrow{A M}=\overrightarrow{b}+\overrightarrow{c}-\dfrac{1}{2} \overrightarrow{a}

.

Câu 11 (1đ):

Cho hàm số $y=f(x)$ có đồ thị hàm số đạo hàm $y=f'(x)$ như trong hình vẽ.

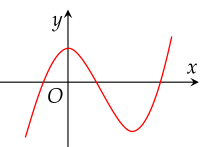
loading...

Số điểm cực trị của hàm số $y=f(x)$ là

4

.

2

.

1

.

3

.

Câu 12 (1đ):

Cho hàm số $y=x^3-3x^2+m$ liên tục và xác định trên $\mathbb{R}$ với $m$ là tham số thực. Gọi giá trị cực đại và giá trị cực tiểu của hàm số đó lần lượt là $T$ và $t$ . Giá trị của $t - T$ bằng

2m-4

.

4-2m

.

4

.

-4

.

Câu 13 (1đ):

Thống kê điểm trung bình cuối năm của các học sinh lớp $11A$ và $11B$ ở bảng sau:

Điểm	$11A$ (học sinh)	$11B$ (học sinh)
$[5;6)$	$1$	$0$
$[6;7)$	$0$	$6$
$[7;8)$	$11$	$8$
$[8;9)$	$22$	$14$
$[9;10)$	$6$	$12$

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Khoảng biến thiên của điểm số học sinh lớp $11A$ là $5$ .
b) Nếu so sánh theo khoảng biến thiên thì điểm trung bình của các học sinh lớp $11B$ ít phân tán hơn điểm trung bình của các học sinh lớp $11A$ .
c) Xét mẫu số liệu của lớp $11A$ ta có độ lệch chuẩn của mẫu số liệu ghép nhóm là $\sqrt{0,51}$ .
d) Nếu so sánh theo độ lệch chuẩn thì học sinh lớp $11A$ có điểm trung bình ít phân tán hơn học sinh lớp $11B$ .

Câu 14 (1đ):

Cho tứ diện $ABCD$ có $AB\,=\,AC=AD=BC=BD=a$ , $\Delta BCD$ vuông cân tại $B$ . Gọi $M$ , $N$ lần lượt là trung điểm các cạnh $AB$ , $CD$ .

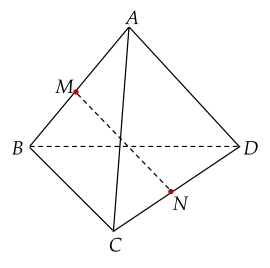
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\overrightarrow{AB}+\overrightarrow{DC}=\overrightarrow{AC}+\overrightarrow{DB}$ .
b) $2\overrightarrow{MN}=\overrightarrow{AC}+\overrightarrow{BD}$ .
c) $\overrightarrow{AB}.\overrightarrow{BC}=\dfrac{1}{2}{a^2}$ .
d) $(\overrightarrow{AD},\overrightarrow{BC})=120^\circ$ .

Câu 15 (1đ):

Một bể chứa $3\,000$ lít nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng độ $25$ gam muối cho một lít nước với tốc độ $20$ lít/phút.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Sau một giờ bơm thì khối lượng muối trong bể là $30$ (kg)
b) Thể tích lượng nước trong bể sau thời gian $t$ phút là $3 \, 000+20t$ (lít)
c) Giả sử nồng độ muối trong nước trong bể sau $t$ phút được được xác định bởi một hàm số $f(t)$ trên $[ 0;+\infty)$ (gam/ lít) thì đường tiệm cận ngang của đồ thị hàm số $y=f\left(t \right)$ là đường thẳng $y=20$ .
d) Khi $t$ càng lớn thì nồng độ muối trong bể tiến gần đến $25$ gam/lít.

Câu 16 (1đ):

Xét hàm số $y=\dfrac{x}{2}-\sin ^2 x$ trên khoảng $(0 ; \pi)$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Hàm số nghịch biến trên khoảng $\Big(\dfrac{5 \pi}{12} ; \pi\Big)$ .
b) Hàm số có hai điểm cực trị.
c) Giá trị cực tiểu của hàm số là $\dfrac{5\pi}{24}-\dfrac{2+\sqrt3}{4}$ .
d) Đồ thị hàm số $y=f'(x)$ cắt đồ thị hàm số $y=\dfrac{-\sin ^2 2 x}{2}$ tại $2$ điểm trên khoảng $(0 ; \pi)$ .

Câu 17 (1đ):

Thời gian truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau:

Thời gian (phút)	Số học sinh
$[9,5;12,5)$	$3$
$[12,5;15,5)$	$14$
$[15,5;18,5)$	$15$
$[18,5;21,5)$	$20$
$[21,5;24,5)$	$4$

Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên bằng bao nhiêu? (Làm tròn kết quả đến chữ số hàng phần trăm)

Trả lời:

Câu 18 (1đ):

Cho biểu đồ thống kê chiều cao của học sinh nữ lớp 12A:

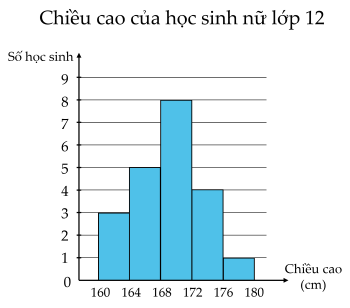
loading...

Tính độ lệch chuẩn của mẫu số liệu trên. (Làm tròn kết quả đến chữ số hàng phần trăm)

Trả lời: .

Câu 19 (1đ):

Trong không gian chọn hệ trục tọa độ cho trước, đơn vị đo lấy kilômét, ra đa phát hiện một máy bay chiến đấu của Anh di chuyển với vận tốc và hướng không đổi từ điểm $M(500;200;10)$ đến điểm $N(800;300;10)$ trong $20$ phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì tọa độ của máy bay sau $4$ phút tiếp là $Q(a;\,b;\,c)$ . Khi đó $a+b+c$ bằng bao nhiêu?

Trả lời:

Câu 20 (1đ):

Một khách sạn có $80$ phòng cho thuê. Người quản lí của khách sạn nhận thấy rằng tất cả các phòng của khách sạn sẽ có người thuê hết nếu giá thuê một phòng là $700 \, 000$ đồng một ngày. Một cuộc khảo sát thị trường cho thấy rằng, trung bình cứ mỗi lần tăng giá thuê phòng thêm $50\,000$ đồng thì sẽ có thêm $2$ phòng bị bỏ trống. Người quản lí nên đặt giá thuê mỗi phòng một ngày là bao nhiêu triệu đồng để doanh thu là lớn nhất? Làm tròn kết quả đến chữ số thập phân thứ hai

Trả lời:

Câu 21 (1đ):

Người ta muốn rào quanh một khu đất với một số vật liệu cho trước là $180$ mét thẳng hàng rào. Ở đó người ta tận dụng một bờ giậu có sẵn để làm một cạnh của hàng rào và rào thành mảnh đất hình chữ nhật. Mảnh đất hình chữ nhật được rào có diện tích lớn nhất bằng bao nhiêu mét vuông?

Trả lời:

Câu 22 (1đ):

Một cốc chứa $20$ ml dung dịch KOH (Potassium Hydroxide) với nồng độ $100$ mg/ml và một bình chứa dung dịch KOH khác với nồng độ $10$ mg/ml. Lấy $x$ (ml) ở bình trộn vào cốc ta được dung dịch KOH có nồng độ $C(x)$ . Coi $C(x)$ là hàm số xác định với $x \geq 0$ . Khi $x \in[5 ; 15]$ , nồng độ của dung dịch KOH đạt giá trị lớn nhất bằng bao nhiêu mg/ml?

Trả lời: mg/ml

Bài học cùng chủ đề

Đề kiểm tra học kì I (đề số 1) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra học kì I (đề số 1) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP