Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra giữa học kì II (đề số 2) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Cho hàm số y=f(x) có bảng xét dấu của đạo hàm như sau:
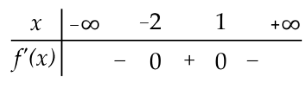
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Khảo sát thời gian tập thể dục của một số học sinh khối 12 thu được mẫu số liệu ghép nhóm sau:
Thời gian (phút) | Số học sinh |
[0;20) | 5 |
[20;40) | 9 |
[40;60) | 12 |
[60;80) | 10 |
[80;100) | 6 |
Nhóm chứa tứ phân vị thứ nhất của mẫu số liệu trên là
Cho hàm số y=f(x) có đồ thị như hình vẽ dưới.
![Giá trị lớn nhất của hàm số trên $[ -3;4 ]$ bằng Giá trị lớn nhất của hàm số trên $[ -3;4 ]$ bằng](https://cdn3.olm.vn/upload/img_teacher/0120/img_teacher_2025-01-20_678d3fca71a19.jpg)
Giá trị lớn nhất của hàm số trên [−3;4] bằng
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ dưới đây:
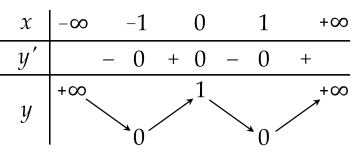
Giá trị cực đại của hàm số đã cho là
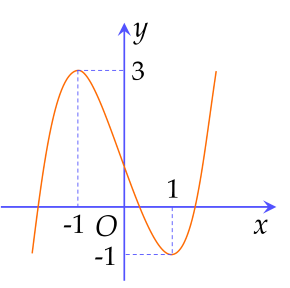
Hàm số nào dưới đây có đồ thị như hình vẽ?
Cho hàm số y=cx+dax+b có đồ thị như hình vẽ dưới.
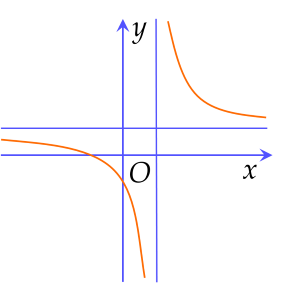
Mệnh đề nào dưới đây đúng?
Tiệm cận ngang của đồ thị hàm số y=x−13 là đường thẳng
Cho tứ diện ABCD có G là trọng tâm tam giác BCD. Mệnh đề nào sau đây sai?
Cho hình chóp S.ABCD có SA⊥(ABCD), đáy ABCD là hình chữ nhật. Biết SA=a. Khoảng cách từ S đến (ABCD) bằng
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A. Biết SA vuông góc với mặt phẳng đáy. Biết SA=BC=a. Thể tích khối chóp S.ABC bằng
Số tiền mà sinh viên chi cho thanh toán cước điện thoại trong tháng:
Số tiền (nghìn đồng) | Số sinh viên |
[0;50) | 5 |
[50;100) | 12 |
[100;150) | 23 |
[150;200) | 17 |
[200;250) | 3 |
Khoảng biến thiên của mẫu số liệu là
Cho tứ diện đều ABCD. Góc giữa hai vectơ AB và CD bằng
Cho hàm số y=f(x)=x3−3x2+1, có đồ thị (C).
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Hàm số y=f(x) có hai điểm cực trị. |
|
| b) Hàm số y=f(x) đồng biến trên khoảng (0;+∞). |
|
| c) Đường thẳng đi qua hai điểm cực trị của đồ thị (C) có phương trình là Δ:y=2x+1 |
|
| d) Đường thẳng d:y=(2m−1)x+m+3 song song với đường thẳng đi qua hai điểm cực trị của đồ thị (C) khi m=2. |
|
Cho hàm số f(x)=x3+ax2+bx+c.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) f(0)=c. |
|
| b) f′(x)=3x2+2ax+b+c. |
|
| c) Nếu f(0)=f′(0) và f(x)≥f′(x)∀x≥−1 thì a=2b. |
|
| d) Nếu f(0)=f′(0), f(x)≥f′(x)∀x≥−1 và f′(x)≥0∀x∈R thì a∈[4;6]. |
|
Trong không gian Oxyz, cho vectơ OA=(2;−1;5) và điểm B(5;−5;7).
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Tọa độ của điểm A là (2;−1;5). |
|
| b) Gọi C(a;b;c) thỏa mãn ΔABC nhận G(1;1;1) làm trọng tâm. Khi đó a+b+c=−4. |
|
| c) Nếu A,B,M(x;y;1) thẳng hàng thì tổng x+y=3. |
|
| d) Cho N∈(Oxy) để ΔABN vuông cân tại A. Tổng hoành độ và tung độ của điểm N bằng 3. |
|
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB=2, AD=4, AA′=7 (tham khảo như hình bên dưới).
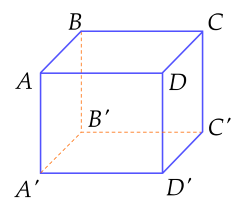
| a) Thể tích khối chóp A.A′B′D′ bằng 28. |
|
| b) Góc giữa đường thẳng AC′ và mặt phẳng (A′B′C′D′) là AC′A′. |
|
| c) Khoảng cách từ điểm A đến mặt phẳng (BB′C′C) bằng 3. |
|
| d) Khoảng cách giữa hai đường thẳng AD′ và DC′ bằng 872829. |
|
Cho hàm số y=−x3+3x+2025. Biết hàm số đồng biến trên khoảng (a;b). Khi đó a2+2b có giá trị bằng bao nhiêu?
Trả lời:
Một khách sạn có 80 phòng cho thuê. Người quản lí của khách sạn nhận thấy rằng tất cả các phòng của khách sạn sẽ có người thuê hết nếu giá thuê một phòng là 700000 đồng một ngày. Một cuộc khảo sát thị trường cho thấy rằng, trung bình cứ mỗi lần tăng giá thuê phòng thêm 50000 đồng thì sẽ có thêm 2 phòng bị bỏ trống. Người quản lí nên đặt giá thuê mỗi phòng một ngày là bao nhiêu triệu đồng để doanh thu là lớn nhất? Làm tròn kết quả đến chữ số thập phân thứ hai
Trả lời:
Trong hệ trục tọa độ Oxyz, cho các điểm A(1;−1;2), B(−1;1;1), C(−3;−3;4), D(1;21;1). Điểm M thay đổi trên mặt phẳng (Oxy). Khi biểu thức T=−3(MDMA)2−2(MDMB)2+(MDMC)2 đạt giá trị lớn nhất thì hoành độ của điểm M bằng bao nhiêu?
Trả lời:
Trong trận đấu bóng đá giữa hai đội Real Madrid và Barcelona, trọng tài cho đội Barcelona được hưởng một quả Penalty. Cầu thủ sút phạt ngẫu nhiên vào 1 trong bốn vị trí 1, 2, 3, 4 và thủ môn bay người cản phá ngẫu nhiên đến 1 trong 4 vị trí 1, 2, 3, 4 với xác suất như nhau (thủ môn và cầu thủ sút phạt đều không đoán được ý định của đối phương). Biết nếu cầu thủ sút và thủ môn bay cùng vào vị trí 1 (hoặc 2) thì thủ môn cản phá được cú sút đó, nếu cùng vào vị trí 3 (hoặc 4) thì xác suất cản phá thành công là 50%. Tính xác suất của biến cố “Cú sút đó không vào lưới” (Kết quả làm tròn đến hàng phần trăm).
Trả lời:
Trong không gian chọn hệ trục tọa độ cho trước, đơn vị đo lấy kilômét, ra đa phát hiện một máy bay chiến đấu của Anh di chuyển với vận tốc và hướng không đổi từ điểm M(500;200;10) đến điểm N(800;300;10) trong 20 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì tọa độ của máy bay sau 4 phút tiếp là Q(a;b;c). Khi đó a+b+c bằng bao nhiêu?
Trả lời:
Một kim tự tháp Khafre ở Ai Cập có dạng hình chóp tứ giác đều với chiều cao 136 m và cạnh đáy dài 152 m. Người ta gắn hệ trục toạ độ như hình vẽ:
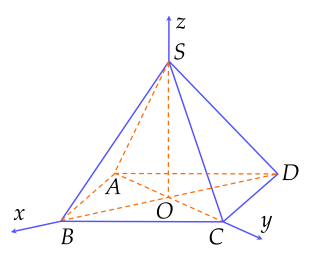
Côsin góc giữa hai mặt bên kề nhau của kim tự tháp bằng (Làm tròn kết quả đến chữ số thập phân thứ hai).
Trả lời:
