Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra giữa học kì I (đề số 3) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Cho hàm số y=x3−3x2−2025. Hàm số đã cho nghịch biến trên khoảng
Cho hàm số y=f(x) liên tục trên R và có đạo hàm f′(x)=x(x+1)2(x+2)3(x+3)4. Hàm số đã cho có bao nhiêu điểm cực trị?
Cho hàm số y=f(x) có bảng biến thiên như sau:

Khẳng định nào sau đây đúng?
Đường tiệm cận đứng của đồ thị hàm số y=2x−22x+1 là
Số giao điểm của đồ thị hàm số y=−2x4+x2+23 và trục hoành là
Đường cong ở hình sau là đồ thị của hàm số nào dưới đây?

Cho biết G là trọng tâm của tứ diện ABCD, mệnh đề nào sau đây đúng?
Trong không gian Oxyz, gọi A′ là hình chiếu vuông góc của điểm A(1;2;3) trên mặt phẳng (Oyz) thì tọa độ AA′ là
Cho ΔABC có AB=AC=5a và BAC=120∘. Độ dài của vectơ tổng AB+AC bằng
Giá trị lớn nhất của hàm số y=−x4+3x2+1 trên [0;2] là
Số tiệm cận của đồ thị hàm số y=x2−3x+2x2−4x−5 là
Tích của giá trị nhỏ nhất và giá trị lớn nhất của hàm số y=f(x)=x+x4 trên đoạn [1;3] bằng
Cho hàm số y=f(x) liên tục và có đồ thị trên đoạn [−2;4] như hình vẽ.
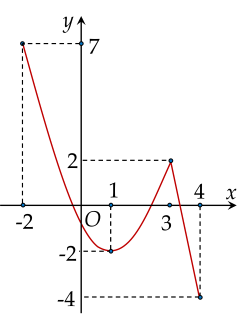
| a) Trên đoạn [−2;4], đồ thị hàm số y=f(x) có 2 điểm cực trị. |
|
| b) Giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [−2;2] là −2. |
|
| c) Giá trị lớn nhất của hàm số y=f(x) trên đoạn [1;4] là −4. |
|
| d) Hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [−2;4] là 11. |
|
Cho hàm số y=f(x) có đồ thị (C) như hình vẽ.

| a) Đồ thị (C) cắt trục Oy tại điểm có tung độ bằng 2. |
|
| b) Đồ thị (C) có tiệm cận đứng là đường thẳng x−1=0. |
|
| c) Hàm số y=f(x) có hai cực trị trong đó yCT>yCĐ. |
|
| d) Hai đường tiệm cận của đồ thị cùng với trục hoành tạo thành tam giác có diện tích bằng 2. |
|
Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong t giờ được cho bởi hàm số có công thức c(t)=t2+1t (mg/L).
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Nồng độ thuốc trong máu của bệnh nhân sau 3 giờ là c(3)=103 (mg/L). |
|
| b) Đạo hàm của hàm số c(t)=t2+1t là c′(t)=(t2+1)21−t2. |
|
| c) Nồng độ thuốc trong máu bệnh nhân tăng trong khoảng t∈(0;2). |
|
| d) Nồng độ thuốc trong máu của bệnh nhân cao nhất khi t=21. |
|
Trong không gian Oxyz, một viên đạn được bắn ra từ vị trí A(1;2;3) hướng đến vị trí B(0;1;−6), bia chắn là mặt phẳng (P):4x−y+2z+13=0, đơn vị là kilômét.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Hình chiếu vuông góc của A trên (Oxy) là H(0;2;3). |
|
| b) Góc giữa đường thẳng AB và mặt phẳng (P) (làm tròn đến hàng đơn vị) là 60∘. |
|
| c) Điểm B thuộc mặt phẳng (P). |
|
| d) Giả sử viên đạn chuyển động thẳng đều theo hướng vectơ v(−2;−2;−18) với vận tốc 800 m/s (bỏ qua mọi lực cản và chướng ngại vật), sau một phút bắn ra đi qua điểm B. |
|
Một cửa hàng kinh doanh rau tươi ước tính doanh thu bởi hàm số f(x)=x2−29000x+1000100000 (đồng) và tiền lãi thu được là g(x)=1000x+100000 (đồng) với x (đồng) là giá bán cho mỗi kg rau tươi. Biết doanh thu bằng tổng tiền lãi và tiền vốn. Tìm giá bán mỗi kg rau tươi (đơn vị nghìn đồng) sao cho cửa hàng phải bỏ vốn ra ít nhất.
Trả lời:
Giả sử chi phí tiền xăng C (đồng) phụ thuộc tốc độ trung bình v(km/h) theo công thức:
C(v)=v16000+25v (0<v≤120)
Để biểu diễn trực quan sự thay đổi của C(v) theo v, người ta đã vẽ đồ thị hàm số C(v) như hình bên.

Tài xế xe tải lái xe với tốc độ trung bình là bao nhiêu để tiết kiệm tiền xăng nhất?
Trả lời:
Có ba lực cùng tác động vào một vật. Hai trong ba lực này hợp với nhau một góc 100∘ và có độ lớn lần lượt là 25 N và 12 N. Lực thứ ba vuông góc với mặt phẳng tạo bởi hai lực đã cho và có độ lớn 4 N. Tính độ lớn của hợp lực của ba lực trên. (làm tròn đến hàng đơn vị)
Trả lời:
Từ một tấm tôn hình chữ nhật có các kích thước là x (m), y (m) với x>1 và y>1 và diện tích bằng 4 m2, người ta cắt bốn hình vuông bằng nhau ở bốn góc rồi gập thành một cái thùng dạng hình hộp chữ nhật không nắp (như hình vẽ) có chiều cao bằng 0,5 m.
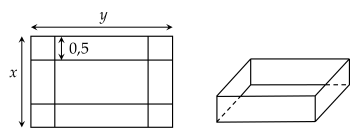
Thể tích của thùng là hàm số V(x) trên khoảng (1;+∞). Đồ thị hàm số y=V(x)1 có bao nhiêu đường tiệm cận đứng?
Trả lời:
Cho hàm số f(x) là hàm số đa thức bậc 4 với đạo hàm f′(x) có đồ thị như hình vẽ.
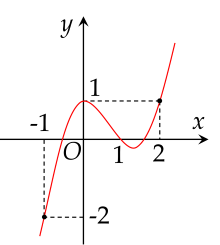
Hàm số g(x)=f(x)−3x3+x2−x+31 có bao nhiêu điểm cực trị?
Trả lời:
Hàm số y=(x+m)3+(x+n)3−x3 đồng biến trên khoảng (−∞;+∞). Giá trị nhỏ nhất của biểu thức P=100[4(m2+n2)−m−n] bằng bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ nhất)
Trả lời:
