Đề ôn tập và kiểm tra giữa học kì I toán 11 cấu trúc mới mới nhất

Câu 1 (1đ):

Câu 2 (1đ):

Dãy số nào sau đây là cấp số cộng?

Dãy số

(b_n)

, với

b_n=\dfrac{1}{2^n-1},\,\forall n\in \mathbb{N}^*

.

Dãy số

(a_n)

, với

a_n=3n-2,\,\forall n \in \mathbb{N}^*

.

Dãy số

(c_n)

, với

c_n=2.3^n, \, \forall n\in \mathbb{N}^*

.

Dãy số

(d_n)

, với

d_n=2+5^n, \, \forall n\in \mathbb{N}^*

.

Câu 3 (1đ):

Nghiệm của phương trình $\cot \dfrac{2x}{3}=\sqrt{3}$ là

x=\dfrac{\pi }{4}+k\pi , \, k\in \mathbb{Z}

.

x=\dfrac{\pi }{2}+\dfrac{3k\pi }{2}, \,k\in \mathbb{Z}

.

x=\dfrac{\pi }{4}+\dfrac{2k\pi }{3}, \,k\in \mathbb{Z}

.

x=\dfrac{\pi }{4}+\dfrac{k3\pi }{2}, \,k\in \mathbb{Z}

.

Câu 4 (1đ):

Giá trị lớn nhất của hàm số $y=3\sin x$ là

3

.

-3

.

2

.

1

.

Câu 5 (1đ):

Trên khoảng $\left(-6\pi ;-5\pi \right)$ , hàm số nào sau đây luôn nhận giá trị dương?

y=\tan x

y=\cos x

.

y=\cot x

.

y=\sin x

.

Câu 6 (1đ):

Khẳng định nào sau đây đúng?

Hàm số

y=\cos x

là hàm số lẻ.

Hàm số

y=\sin x

là hàm số chẵn.

Hàm số

y=\cot x

là hàm số chẵn.

Hàm số

y=\tan x

là hàm số lẻ.

Câu 7 (1đ):

Câu 8 (1đ):

Giá trị của các hàm số lượng giác $\sin \dfrac{5\pi }{4}$ ; $\sin \dfrac{5\pi }{3}$ lần lượt bằng

\dfrac{\sqrt{2}}{2}; \, \dfrac{-\sqrt{3}}{2}

.

\dfrac{-\sqrt{2}}{2}; \, \dfrac{\sqrt{3}}{2}

.

\dfrac{-\sqrt{2}}{2}; \, \dfrac{-\sqrt{3}}{2}

.

\dfrac{\sqrt{2}}{2}; \, \dfrac{\sqrt{3}}{2}

.

Câu 9 (1đ):

Tìm hiểu thời gian hoàn thành một bài kiểm tra đánh giá thường xuyên (đơn vị: phút) của một số học sinh thu được kết quả sau:

Thời gian (phút)	$\left[ 10;11 \right)$	$\left[ 11;12 \right)$	$\left[ 12;13 \right)$	$\left[ 13;14 \right)$	$\left[ 14;15 \right)$
Số học sinh	$1$	$2$	$5$	$12$	$20$

Thời gian trung bình (phút) để hoàn thành bài kiểm tra của các em học sinh là

10,5

.

14,5

.

13,7

.

12,3

.

Câu 10 (1đ):

Cho cấp số cộng $(u_n)$ thoả mãn $\left\{ \begin{aligned} u_2-u_3+u_5=10 \\ u_4+u_6=26\\ \end{aligned} \right.$ . Giá trị $S=u_1+u_5+u_9+...+u_{2 \, 021}$ bằng

1 \, 533 \, 686

.

6 \, 730 \, 444

.

2 \, 023 \, 563

.

6 \, 734 \, 134

.

Câu 11 (1đ):

Cho phương trình $\cos \left(2x-\dfrac{\pi }{3} \right)-m=2$ . Giá trị của $m$ để phương trình có nghiệm là

m\in \left[ -3;-1 \right]

.

m\in \left[ -1;3 \right]

.

m\in \mathbb{R}

.

m \in \varnothing

.

Câu 12 (1đ):

Cho $\sin a=\dfrac{3}{5}$ ; $\cos a<0$ ; $\cos b=\dfrac{3}{4}$ ; $\sin b>0$ . Giá trị $\sin (a-b)$ bằng

-\dfrac{1}{5}\Big(\sqrt{7}+\dfrac{9}{4} \Big).

\dfrac{1}{5}\Big(\sqrt{7}+\dfrac{9}{4} \Big).

-\dfrac{1}{5}\Big(\sqrt{7}-\dfrac{9}{4} \Big).

\dfrac{1}{5}\Big(\sqrt{7}-\dfrac{9}{4} \Big).

Câu 13 (1đ):

Cho mẫu số liệu ghép nhóm về lương của nhân viên trong một công ty như sau:

Lương (triệu đồng)	$[9 ; 12)$	$[12 ; 15)$	$[15 ; 18)$	$[18 ; 21)$	$[21 ; 24)$
Số nhân viên	$6$	$12$	$4$	$2$	$1$

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Giá trị đại diện của nhóm $\left[ 9;12 \right)$ là $10,5$ .
b) Trung bình lương các nhân viên là $16,5$ triệu đồng.
c) Nhóm chứa trung vị là $\left[ 15;18 \right)$ .
d) Tứ phân vị thứ ba là $15,56$ .

Câu 14 (1đ):

Cho dãy số $(u_n)$ có số hạng tổng quát $u_n=\dfrac{n}{4^n}$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Ta có $u_n=\dfrac{n}{4^n}<0, \, \forall n \in \mathbb{N}^*$ .
b) Ta có $\dfrac{u_{n+1}}{u_n}<1, \, \forall n\ge 1$ .
c) Ta có $u_{2 \, 024}<u_{2 \, 023}$ .
d) Dãy số $(u_n)$ là dãy số tăng.

Câu 15 (1đ):

Một vật dao động xung quanh vị trí cân bằng theo phương trình $x=1,5\cos \Big(\dfrac{t\pi }{4}\Big)$ ; trong đó $t$ là thời gian được tính bằng giây và quãng đường $h=|x|$ được tính bằng mét là khoảng cách theo phương ngang của vật đối với vị trí cân bằng.

loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Vật ở xa vị trí cân bằng nhất nghĩa là $h=1,5$ m.
b) Trong $10$ giây đầu tiên, có hai thời điểm vật ở xa vị trí cân bằng nhất.
c) Khi vật ở vị trí cân bằng thì $\cos \Big( \dfrac{t\pi }{4} \Big)=0$ .
d) Trong khoảng từ $0$ đến $20$ giây thì vật đi qua vị trí cân bằng $4$ lần.

Câu 16 (1đ):

Anh Bình là nhân viên của một công ty A. Từ ngày 1/2/2024 anh Bình được nâng lương lên bậc 4, mức lương anh hiện hưởng là $11$ $718$ $750$ đồng mỗi tháng. Theo quy định của công ty, nếu không bị kỉ luật, không có khen thưởng đặc biệt thì cứ sau $3$ năm anh Bình sẽ được nâng một bậc lương, tăng thêm $25\%$ so với bậc lương trước, tối đa là bậc 7. Khi hết bậc 7 sẽ chuyển sang vượt khung. Lương vượt khung năm sau cao hơn năm trước $1\%$ và vẫn nhận hàng tháng. Lương bậc 1 sẽ được tính sau khi hết đúng $1$ năm tập sự. Anh Bình là người rất nghiêm túc, không vi phạm kỉ luật. Anh dự định sẽ làm việc $30$ năm ở công ty này rồi nghỉ hưu.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Lương bậc 5 của anh Bình sẽ là $14$ $500$ $000$ đồng.
b) Lương bậc 1 của anh Bình là $6$ $000$ $000$ đồng.
c) Lương bậc 7 anh Bình là $23$ $250$ $000$ .
d) Tổng tiền lương anh Bình nhận được kể từ khi hết tập sự đến khi nghỉ hưu là $5 \, 554 \, 357 \, 709$ .

Câu 17 (1đ):

Nguời ta thiết kế một cái tháp gồm $10$ tầng theo cách: Diện tích bề mặt trên của mỗi tầng bằng nửa diện tích bề mặt trên của tầng ngay bên dưới và diện tích bề mặt của tầng $1$ bằng nửa diện tích bề mặt đế tháp. Biết diện tích bề mặt đế tháp là $12 \, 288$ m $^2$ , tính diện tích bề mặt trên cùng của tháp (đơn vị mét vuông).

Trả lời:

Câu 18 (1đ):

Sinh nhật bạn của An vào ngày $1$ tháng năm. An muốn mua một món quà sinh nhật cho bạn thân của mình nên quyết định bỏ ống heo $1 \, 000$ đồng vào ngày $01$ tháng $01$ năm $2016$ , sau đó cứ liên tục ngày sau hơn ngày trước $1 \, 000$ đồng. Đến ngay trước ngày sinh nhật của bạn thân, An đã tích lũy được bao nhiêu tiền? (ghi kết quả dưới dạng số thập phân, đơn vị nghìn đồng)

Trả lời:

Câu 19 (1đ):

Số giờ có ánh sáng của một thành phố $A$ trong ngày thứ $t$ của năm $2025$ được cho bởi một hàm số $y=4\sin \Big| \dfrac{\pi }{178}( t-60) \Big|+10$ , với $t \in \mathbb{Z}$ và $60<t\le 365$ . Vào ngày thứ bao nhiêu trong năm đó thì thành phố $A$ có nhiều giờ ánh sáng mặt trời nhất?

Trả lời:

Câu 20 (1đ):

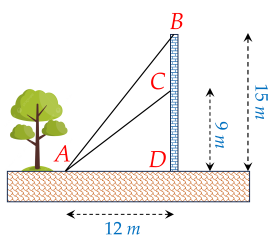
loading...

Từ một vị trí $A$ , người ta buộc hai sợi cáp $AB$ và $AC$ đến một cái trụ cao $15$ m, được dựng vuông góc với mặt đất, chân trụ ở vị trí $D$ . Biết $CD=9$ m và $AD=12$ m. Tìm góc nhọn $\alpha =\widehat{BAC}$ tạo bởi hai sợi dây cáp đó, đồng thời tính gần đúng $\alpha$ (làm tròn đến hàng phần mười, đơn vị độ).

Trả lời:

Câu 21 (1đ):

Câu 22 (1đ):

Cho hình vuông $(C_1)$ có cạnh bằng $a$ . Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông $(C_2)$ .

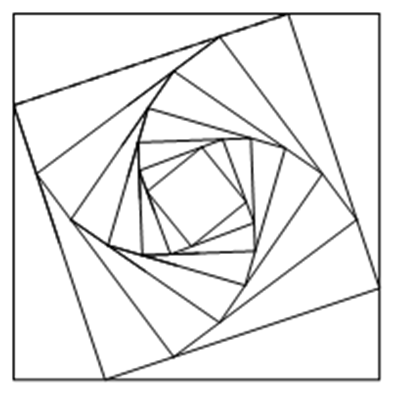
Từ hình vuông $(C_2)$ lại tiếp tục làm như trên ta nhận được dãy các hình vuông $C_1$ , $C_2$ , $C_3$ ,..., $C_n$ . Gọi $S_i$ là diện tích của hình vuông $C_i, \, (i \in \left\{ 1;2;3,..... \right\})$ . Đặt $T=S_1+S_2+S_3+...+S_n+...$ . Biết $T=\dfrac{32}{3}$ , tính $a$ ?

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra giữa học kì I (đề số 3) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra giữa học kì I (đề số 3) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP