Kiến thức nền tảng: Hàm số và đồ thị SVIP

1. Hàm số y = ax² (a khác 0)

Hàm số  $y=ax^2 (a \ne 0)$ xác định với mọi giá trị $x$ thuộc $\mathbb{R}$.

Ví dụ 1. Cho hàm số $y=\dfrac{3}{2}x^2$. Hoàn thành bảng giá trị sau:

Lời giải

2. Đồ thị hàm số y = ax² (a khác 0)

Cách vẽ đồ thị hàm số y = ax² (a khác 0)

⚡️Bước 1: Lập bảng ghi một số giá trị tương ứng giữa $x$ và $y$.

⚡️Bước 2: Biểu diễn các cặp điểm $(x;y)$ trong bảng giá trị trên trong mặt phẳng $Oxy$ và nối chúng lại để được một đường cong là đồ thị của hàm số $y=ax^2 (a \ne 0)$.

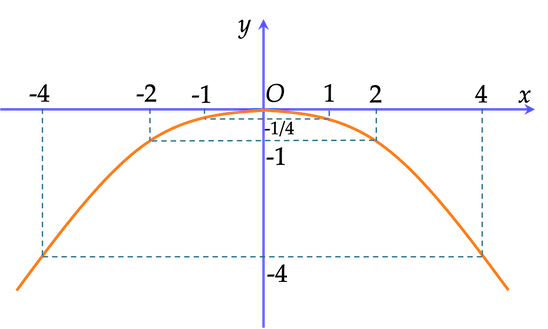
​Ví dụ 2. Vẽ đồ thị của hàm số $y=-\dfrac{1}{4}x^2$.

Lời giải

Lập bảng một số giá trị tương ứng giữa $x$ và $y$.

Biểu diễn các điểm $(-4;-4); \, (-2;-1); \, \Big(-1; -\dfrac{1}{4} \Big); \, (0:0); \, (4;-4); \, (2;-1); \, \Big(1; -\dfrac{1}{4} \Big)$ trên mặt phẳng toạ độ $Oxy$ và nối chúng lại ta được đồ thị hàm số $y=-\dfrac{1}{4}x^2$ như hình vẽ.

Tính đối xứng của đồ thị hàm số y = ax² (a khác 0)

Đồ thị của hàm số $y=ax^2 (a \ne 0)$ là một đường cong, gọi là đường parabol, có các tính chất sau:

⚡️Có đỉnh là gốc toạ độ $O$.

⚡️Có trục đối xứng là $Oy$.

⚡️Nằm phía trên trục hoành nếu $a>0$ và nằm phía dưới trục hoành nếu $a<0$.

Ví dụ 3. a) Vẽ đồ thị hàm số $y=-2x^2$.

b) Tìm toạ độ các điểm thuộc đồ thị có tung độ bằng $-\dfrac{1}{2}$ và nhận xét về tính đối xứng giữa các điểm đó.

Lời giải

a) Lập bảng một số giá trị tương ứng giữa $x$ và $y$:

Biểu diễn các điểm $(-2;-8); \, (-1; -2); \, (0:0); \, (2;-8); \, (1; -2)$ trên mặt phẳng toạ độ $Oxy$ và nối chúng lại ta được đồ thị hàm số  $y=-2x^2$ như hình vẽ.

b) Ta có: $y=-\dfrac{1}{2}$ nên $-2x^2=-\dfrac{1}{2}$ hay $x^2=\dfrac{1}{4}$.

Suy ra $x=\dfrac{1}{2}$ hoặc $x=-\dfrac{1}{2}$.

Vậy có điểm cần tìm là $\Big( \dfrac{1}{2}; -\dfrac{1}{2} \Big)$ và $\Big( -\dfrac{1}{2}; -\dfrac{1}{2} \Big)$. Hai điểm này đối xứng với nhau qua trục $Oy$.

Chú ý: Hai điểm $(x;y)$ và $(-x;y)$ đối xứng với nhau qua trục tung $Oy$.

3. Tương giao giữa các đồ thị hàm số

Cho parabol $(P): \, y = ax^2$; ($a \ne 0$) và đường thẳng $(d): \, y = bx + c$. Để tìm tọa độ giao điểm của $(P)$ và $d$ ta làm như sau:

+ Xét phương trình hoành độ giao điểm của $(P)$ và $d$ ta được: $ax^2 = bx + c$ (*). Giải phương trình (*) để tìm nghiệm (nếu có).

+ Thay giá trị $x$ tìm được vào một trong hai phương trình $(P)$ hoặc $d$ để tìm giá trị của $y$. Từ đó tìm tọa độ giao điểm của $(P)$ và $d$.

Số nghiệm của (*) bằng đúng số giao điểm của $(P)$ và $d$:

+ Nếu (*) vô nghiệm thì $d$ không cắt $(P)$;

+ Nếu (*) vô nghiệm thì $d$ không cắt $(P)$;

+ Nếu (*) có hai nghiệm phân biệt thì $d$ cắt $(P)$ tại hai điểm phân biệt.

Ví dụ 4. Cho parabol $(P): y = x^2$ và đường thẳng $d: y = 2(m - 1)x + 2m + 3$. Chứng minh rằng với mọi $m$ đường thẳng $d$ luôn cắt parabol $(P)$ tại hai điểm phân biệt $A$, $B$. Giả sử $A(x_A ; y_A), \, B(x_B ; y_B)$, tìm $m$ để $x_A^2 + x_B^2 = 10$.

Lời giải

Phương trình hoành độ giao điểm của $d$ và $(P)$ là: $x^2  = 2(m - 1)x + 2m + 3$

$x^2 - 2(m - 1)x - 2m - 3 = 0$ (*)

Ta có: $\Delta  = (m - 1)^2 + 2m + 3 =  m^2 - 2m + 1 + 2m + 3 = m^2 + 4$

Vì $m^2 \ge 0$ với mọi $m$ nên $\Delta = m^2 + 4 \ge 4 > 0$ với mọi $m$.

Vậy phương trình (*) có hai nghiệm phân biệt (giả sử là $x_1$; $x_2$) với mọi $m$;

Suy ra đường thẳng $d$ luôn cắt $(P)$ tại hai điểm phân biệt (gọi là $A$, $B$) với mọi $m$.

Áp dụng định lí Viète, ta có: $x_1 + x_2 = 2(m - 1)$ và $x_1 x_2  = -2m - 3$.

Hay $x_A + x_B = 2(m - 1)$ và $x_A x_B  = -2m - 3$

Mà $x_A^2 + x_B^2 = 10$ nên nên $(x_A + x_B)^2 – 2x_Ax_B = 10$

hay $4(m - 1)^2 - 2(-2m - 3) = 10$

$4m^2 - 8m + 4 + 4m + 6 = 10$

$4m^2 - 4m = 0$

$m = 0$ hoặc $m = 1$ (thỏa mãn điều kiện)

Vậy $m = 0$; $m = 1$ là các giá trị cần tìm.