Các trường hợp đồng dạng của hai tam giác vuông (vận dụng) SVIP

Cho tam giác $ABC$ vuông tại $A$, $AB = 16$ cm, $AC = 12$ cm. Kẻ tia $Cx$ vuông góc với $BC$ (tia $Cx$ và điểm $A$ khác phía so với đường thẳng $BC$). Trên tia $Cx$ lấy điểm $D$ sao cho $BD = 25$ cm. Chứng minh rằng $BD$ // $AC$.

Điền kí hiệu thích hợp vào ô trống để hoàn thành bài giải.

Xét tam giác vuông $ABC$, áp dụng định lí Pythagore ta có: suy ra $BC=20$ (cm).

Xét tam giác vuông ABC và tam giác vuông CDB có:

Vậy $\Delta ABC\backsim\Delta CDB$ (Cạnh huyền - cạnh góc vuông).

Suy ra

Lại thấy hai góc trên ở vị trí , nên $BD$ // $AC$.

Cho hình vẽ, có bao nhiêu cặp tam giác vuông đồng dạng?

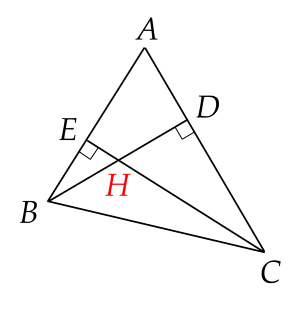
Cho $\Delta ABC$ nhọn, hai đường cao $BD$ và $CE$ cắt nhau tại $H$. Có bao nhiêu cặp tam giác vuông đồng dạng?

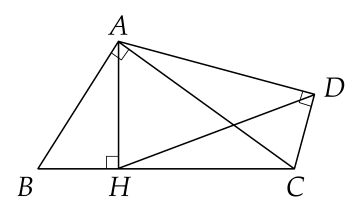
Cho hình vẽ, chọn câu trả lời đúng.

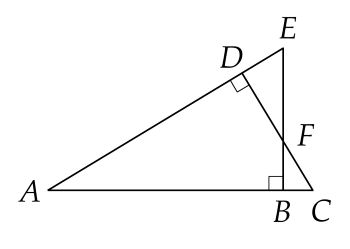
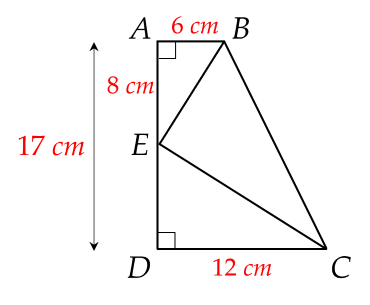
Cho hình vẽ, khi đó $\widehat{BEC}$ bằng

Cho hình chữ nhật $ABCD$ có $AB=12$ cm; $BC=9$ cm. Gọi $H$ là chân đường vuông góc kẻ từ $A$ xuống $BD$. Diện tích $\Delta AHB$ bằng

Cho $\Delta ABC$ vuông tại $A$, đường cao $AH$ có $BC=20$ cm; $AC=12$ cm.

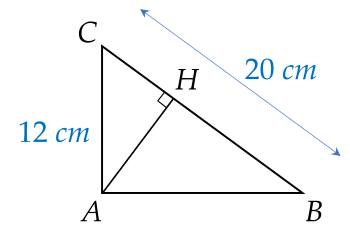
Độ dài $BH$ bằng

Cho $\Delta ABC$ vuông tại $A \, (AB<AC)$, đường cao $AH$, đường trung tuyến $AM$. Biết $\dfrac{AH}{AM}=\dfrac{12}{13}$. Tỉ số $\dfrac{AB}{AC}$ bằng

Cho $\Delta ABC$ vuông tại $A$, đường cao $AH$, đường trung tuyến $AM$. Biết $BH=4$ cm, $CH=9$ cm. Diện tích $\Delta AHM$ bằng

Cho tam giác $ABC$ vuông tại $C$. $D$ thuộc cạnh $CB$. $E$ là hình chiếu của $B$ trên đường thẳng $AD$. Khẳng định nào dưới đây sai?

Cho tam giác $ABC$ vuông tại $A$ có $AC = 8$ cm, $BC = 14$ cm. Đường trung trực của $BC$ cắt đường thẳng $AC$ tại $N$. Tìm độ dài $CN$.

Đáp số: $CN =$

Cho hình vẽ:

Mỗi khẳng định dưới đây đúng hay sai?

Cho tam giác $ABC$ vuông tại $B$. Đường cao $BH$ chia cạnh huyền thành hai đoạn $AH = 36$ cm và $CH = 25$ cm. Tính diện tích tam giác $ABC$.

Đáp số: $S_{ABC}=$

Cho tam giác $ABC$ và tam giác $A'B'C'$, $\widehat{ABC}=\widehat{A'B'C'}=90^\circ$, hai đường cao lần lượt là $BH$ và $B'H'$. Biết rằng $\dfrac{BH}{BA}=\dfrac{B'H'}{B'A'}.$ Chứng minh $\Delta ABC\backsim\Delta A'B'C.$

Sắp xếp các bước chứng minh để được bài chứng minh đúng

• Khi đó $\widehat{BAH}=\widehat{B'A'H'}$.
• Xét tam giác vuông $ABC$ và tam giác vuông $A'B'C'$ có: $\widehat{BAC}=\widehat{B'A'C'}$.
• Xét tam giác vuông $ABH$ và tam giác vuông $A'B'H'$ có: $\dfrac{BH}{BA}=\dfrac{B'H'}{B'A'}$.
• Suy ra $\Delta ABH\backsim\Delta A'B'H'$ (c.g.c).
• Suy ra $\Delta ABC\backsim\Delta A'B'C'$ (g.g).

Cho hình vẽ. Chứng minh $\widehat{BEC}=90^\circ$.

Sắp xếp các bước để được bài chứng minh đúng.