Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu không ghép nhóm SVIP
I. SỐ TRUNG BÌNH CỘNG (SỐ TRUNG BÌNH)
1. Định nghĩa
Số trung bình cộng của một mẫu \(n\) số liệu thống kê bằng tổng của các số liệu chia cho số các số liệu đó. Số trung bình cộng của mẫu số liệu \(x_1,x_2,...,x_n\) bằng
\(\overline{x}=\dfrac{x_1+x_2+...+x_n}{n}.\)
Nhận xét:
- Khi mẫu số liệu được cho dưới dạng bảng tần số
| Giá trị | \(x_1\) | \(x_2\) | \(...\) | \(x_k\) |
| Tần số | \(n_1\) | \(n_2\) | \(...\) | \(n_k\) |
Công thức tính số trung bình là:
\(\overline{x}=\dfrac{x_1n_1+x_2n_2+...+x_kn_k}{n_1+n_2+...+n_k}\)
- Khi mẫu số liệu cho bởi bảng phân bố tần số tương đối
| Giá trị | \(x_1\) | \(x_2\) | \(...\) | \(x_k\) |
| Tần số tương đối | \(f_1\) | \(f_2\) | \(...\) | \(f_k\) |
Công thức tính số trung bình là:
\(\overline{x}=f_1x_1+f_2x_2+...+f_kx_k.\)
Trong đó \(f_1=\dfrac{n_1}{n};f_2=\dfrac{n_2}{n};...;f_k=\dfrac{n_k}{n}\) với \(n=n_1+n_2+...+n_k.\)
2. Ý nghĩa
Khi các số liệu trong mẫu ít sai lệch so với số trung bình cộng, ta có thể lấy số trung bình cộng làm đại diện cho mẫu số liệu.
Ví dụ 1. Cho bảng phân bố tần số
Khối lượng \(30\) quả trứng gà trong một rổ trứng gà
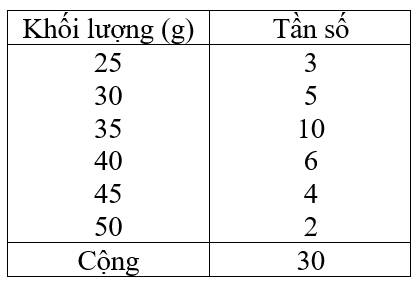
Tính khối lượng trung bình của mỗi quả trứng gà.
Giải
Khối lượng trung bình của mỗi quả trứng gà là
\(\overline{X}=\dfrac{25.3+30.5+35.10+40.6+45.4+50.2}{30}=36,5\) (g)
II. TRUNG VỊ
1. Định nghĩa
Sắp thứ tự mẫu số liệu gồm \(n\) số liệu thành một dãy không giảm (hoặc không tăng).
- Nếu \(n\) là số lẻ thì số liệu đứng ở vị trí thứ \(\dfrac{n+1}{2}\) (số đứng chính giữa) gọi là trung vị.
- Nếu \(n\) là chẵn thì số trung bình cộng của hai số liệu đứng ở vị trí thứ \(\dfrac{n}{2}\) và \(\dfrac{n}{2}+1\) gọi là trung vị.
Trung vị kí hiệu là \(M_e\).
Nhận xét:
- Trung vị không nhất thiết là một số trong mẫu số liệu và dễ tính toán.
- Khi các số liệu trong mẫu không có sự chênh lệch lớn thì số trung bình cộng và trung vị xấp xỉ nhau.
Ví dụ 2: Tìm số trung vị cho mẫu số liệu ở ví dụ 1?
Giải
Sắp xếp mẫu số liệu theo thứ tự

Do số giá trị của mẫu số liệu là \(30\) nên số trung vị là trung bình cộng của hai giá trị thứ \(15\) (có giá trị là \(35\)) và \(16\) (có giá trị là \(35\)) của mẫu số liệu vậy số trung vị là \(\dfrac{35+35}{2}=35.\)
2. Ý nghĩa
Nếu những số liệu trong mẫu có sự chênh lệch lớn thì ta chọn trung vị làm đại diện cho mẫu số liệu đó. Những kết luận về đối tượng thống kê rút ra khi đó sẽ tin cậy hơn.
III. TỨ PHÂN VỊ
1. Định nghĩa
Sắp thứ tự mẫu số liệu gồm \(N\) số liệu thành một dãy không giảm.
Tứ phân vị của mẫu số liệu trên là bộ ba giá trị: tứ phân vị thứ nhất, tứ phân vị thứ hai và tứ phân vị thứ ba; ba giá trị này chia mẫu số liệu thành bốn phần tử có số lượng phần tử bằng nhau.
- Tứ phân vị thứ hai \(Q_2\) bằng trung vị.
- Nếu \(N\) là số chẵn thì tứ phân vị thứ nhất \(Q_1\) bằng trung vị của nửa dãy phía dưới và tứ phân vị thứ ba \(Q_3\) bằng trung vị của nửa dãy phía trên.
- Nếu \(N\) là số lẻ thì tứ phân vị thứ nhất \(Q_1\) bằng trung vị của nửa dãy phía dưới (không bao gồm \(Q_2\)) và tứ phân vị thứ ba \(Q_3\) bằng trung vị của nửa dãy phía trên (không bao gồm \(Q_2\)).
Ví dụ 3. Thời gian đọc sách (đơn vị giờ) trong một ngày của một số học sinh lớp 10 được cho như sau:
| 1 | 2 | 0 | 1 | 3 | 2 | 4 | 0 | 2 | 3 |
Hãy tìm các tứ phân vị?
Giải
Sắp xếp các giá trị theo thứ tự không giảm
| 0 | 0 | 1 | 1 | 2 | 2 | 2 | 3 | 3 | 4 |
Vì \(n=10\) là số chẵn nên \(Q_2\) là trung bình cộng của hai giá trị chính giữa:
\(Q_2=\dfrac{2+2}{2}=2\).
\(Q_1\) là trung vị của nửa số liệu bên trái \(Q_2\):
| 0 | 0 | 1 | 1 | 2 |
tìm được \(Q_1\) là giá trị chính giữa, \(Q_1=1.\)
\(Q_3\) là trung vị của nửa số liệu bên phải \(Q_2\):
| 2 | 2 | 3 | 3 | 4 |
tìm được \(Q_3\) là giá trị chính giữa, \(Q_3=3.\)
2. Ý nghĩa
Ba giá trị \(Q_1,Q_2,Q_3\) trong tứ phân vị phản ánh độ phân tán của mẫu số liệu. Nhưng mỗi giá trị \(Q_1,Q_2,Q_3\) lại đo xu thế trung tâm của phần số liệu tương ứng của mẫu đó.
IV. MỐT
1. Định nghĩa
Mốt của mẫu số liệu là giá trị có tần số lớn nhất trong bảng phân bố tần số và kí hiệu là \(M_0\).
Chú ý: Một mẫu số liệu có thể có một hoặc nhiều mốt.
2. Ý nghĩa
Mốt của mẫu số liệu đặc trưng cho số lần lặp đi lặp lại nhiều nhất tại một vị trí của mẫu số liệu đó. Dựa vào mốt, ta có thể đưa ra những kết luận (có ích) về đối tượng thống kê.
Ví dụ 4. Hãy tìm mốt trong mẫu số liệu ở ví dụ 1 và ví dụ 3.
Giải
Trong ví dụ 1, vì số trứng gà có khối lượng \(35\) g là nhiều nhất (\(10\) quả) nên mốt là \(35\).
Trong ví dụ 3, vì số học sinh đọc \(2\) tiếng mỗi ngày là lớn nhất (\(3\) học sinh) nên mốt là \(2\).
Bạn có thể đăng câu hỏi về bài học này ở đây
