Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Các số đặc trưng đo độ phân tán SVIP
1. KHOẢNG BIẾN THIÊN VÀ KHOẢNG TỨ PHÂN VỊ
a. Khoảng biến thiên
Khoảng biến thiên, kí hiệu là \(R\), là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất trong mẫu số liệu.
Ý nghĩa. Khoảng biến thiên dùng để đo độ phân tán của mẫu số liệu. Khoảng biến thiên càng lớn thì mẫu số liệu càng phân tán.
Ví dụ 1. Cho mẫu số liệu:
| \(5\) | \(6\) | \(4\) | \(7\) | \(6\) | \(8\) | \(5\) | \(6\) |
Tìm khoảng biến thiên của mẫu số liệu này.
Giải
Giá trị cao nhất và thấp nhất của mẫu số liệu lần lượt là \(8\) và \(4\), do đó khoảng biến thiên là \(R=8-4=4.\)
Nhận xét. Sử dụng khoảng biến thiên có ưu điểm là đơn giản, dễ tính toán nhưng khoảng biến thiên chỉ sử dụng thông tin của giá trị lớn nhất và giá trị nhỏ nhất mà bỏ qua các giá trị khác nên khoảng biến thiên dễ bị ảnh hưởng bởi các giá trị bất thường.
b. Khoảng tứ phân vị
Khoảng tứ phân vị, kí hiệu là \(\Delta_Q\) là hiệu số giữa tứ phân vị thứ ba và tứ phân vị thứ nhất:
\(\Delta_Q=Q_3-Q_1\).
Ý nghĩa. Khoảng tứ phân vị cũng là một số đo độ phân tán của mẫu số liệu. Khoảng tứ phân vị càng lớn thì mẫu số liệu càng phân tán.
Chú ý. Một số tài liệu còn gọi khoảng biến thiên là biên độ và khoảng tứ phân vị là độ trái giữa.
Ví dụ 2. Cho mẫu số liệu điểm kiểm tra môn Toán của một tổ:
| \(9\) | \(8\) | \(8\) | \(7\) | \(6\) | \(9\) | \(7\) | \(10\) | \(8\) |
Tìm khoảng tứ phân vị cho mẫu số liệu này.
Giải
Sắp xếp mẫu số liệu theo thứ tự không giảm
| \(6\) | \(7\) | \(7\) | \(8\) | \(8\) | \(8\) | \(9\) | \(9\) | \(10\) |
Mẫu số liệu có \(9\) giá trị nên trung vị là số chính giữa, \(Q_2=8\).
\(Q_1=\dfrac{7+7}{2}=7;Q_3=\dfrac{9+9}{2}=9;\)
Vậy khoảng tứ phân vị của mẫu số liệu trên là \(\Delta_Q=Q_3-Q_1=9-7=2.\)
2. PHƯƠNG SAI VÀ ĐỘ LỆCH CHUẨN
Phương sai là giá trị \(s^2=\dfrac{\left(x_1-\overline{x}\right)^2+\left(x_2-\overline{x}\right)^2+...+\left(x_n-\overline{x}\right)^2}{n}\)
Căn bậc hai của phương sai, \(s=\sqrt{s^2}\), được gọi là độ lệch chuẩn.
Chú ý. Người ta còn sử dụng đại lượng để đo độ phân tán của mẫu số liệu:
\(\widehat{s}^2=\dfrac{\left(x_1-\overline{x}\right)^2+\left(x_2-\overline{x}\right)^2+...+\left(x_n-\overline{x}\right)^2}{n-1}\)
Ý nghĩa. Nếu số liệu càng phân tán thì phương sai và độ lệch chuẩn càng lớn.
Ví dụ 3. Mẫu số liệu sau đây cho biết cân nặng của \(5\) bạn lớp \(10\) (đơn vị kg):
| \(45\) | \(48\) | \(46\) | \(50\) | \(48\) |
Tìm phương sai và độ lệch chuẩn cho mẫu số liệu này.
Giải
Số trung bình của mẫu số liệu là
\(\overline{X}=\dfrac{45+48+46+50+48}{5}=47,4\)
Phương sai của mẫu số liệu là
\(s^2=\dfrac{\left(45-47,4\right)^2+\left(48-47,4\right)^2+\left(46-47,4\right)^2+\left(50-47,4\right)^2+\left(48-47,4\right)^2}{5}=3,04\)
Độ lệch chuẩn \(s=\sqrt{s^2}\approx1,74.\)
3. PHÁT HIỆN SỐ LIỆU BẤT THƯỜNG HOẶC KHÔNG CHÍNH XÁC BẰNG BIỂU ĐỒ HỘP
Trong mẫu số liệu thống kê, có khi gặp những giá trị quá lớn hoặc quá nhỏ so với đa số các giá trị khác. Những giá trị này được gọi là giá trị bất thường, ta có thể dùng biểu đồ hộp để phát hiện những giá trị bất thường này.
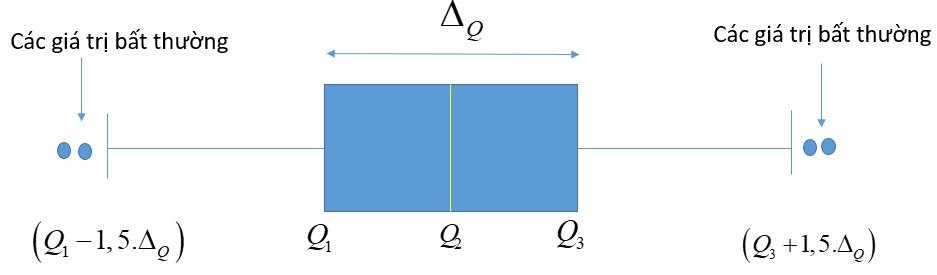
Các giá trị lớn hơn \(Q_3+1,5.\Delta_Q\) hoặc bé hơn \(Q_1-1,5.\Delta_Q\) được xem là giá trị bất thường.
Ví dụ 4. Một mẫu số liệu có tứ phân vị thứ nhất là \(48\) và tứ phân vị thứ ba là \(76\). Hãy kiểm tra xem trong hai giá trị \(5\) và \(100\) giá trị nào được xem là giá trị bất thường.
Giải
Ta có \(Q_1=48;Q_3=76\Rightarrow\Delta_Q=Q_3-Q_1=76-48=28\)
Khi đó \(Q_1-1,5.\Delta_Q=6;Q_3+1,5.\Delta_Q=118\)
nên \(5\) (nhỏ hơn \(6\)) là một giá trị bất thường của mẫu số liệu.
Bạn có thể đăng câu hỏi về bài học này ở đây
