Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Bài tập tự luận: Hình chữ nhật SVIP
Cho tam giác $ABC$, đường cao $AH$. Gọi $I$ là trung điểm của $AC$. Lấy $D$ thuộc tia $HI$ sao cho $IH = ID$. Chứng minh tứ giác $AHCD$ là hình chữ nhật.
Hướng dẫn giải:
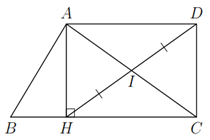
Ta có $IA=IC$ và $IH=ID$.
Suy ra $AHCD$ là hình bình hành do có hai đường chéo $AC$ và $DH$ cắt nhau tại trung điểm $I$.
Mà $\widehat{AHC}=90^\circ$ suy ra $AHCD$ là hình chữ nhật.
Cho hình thang vuông $ABCD$ có $\widehat{A}=\widehat{D}={{90}^{\circ}}$. Gọi $M$ là trung điểm của $AC$ và $BM = \dfrac{1}{2}AC$. Chứng minh tứ giác $ABCD$ là hình chữ nhật.
Hướng dẫn giải:
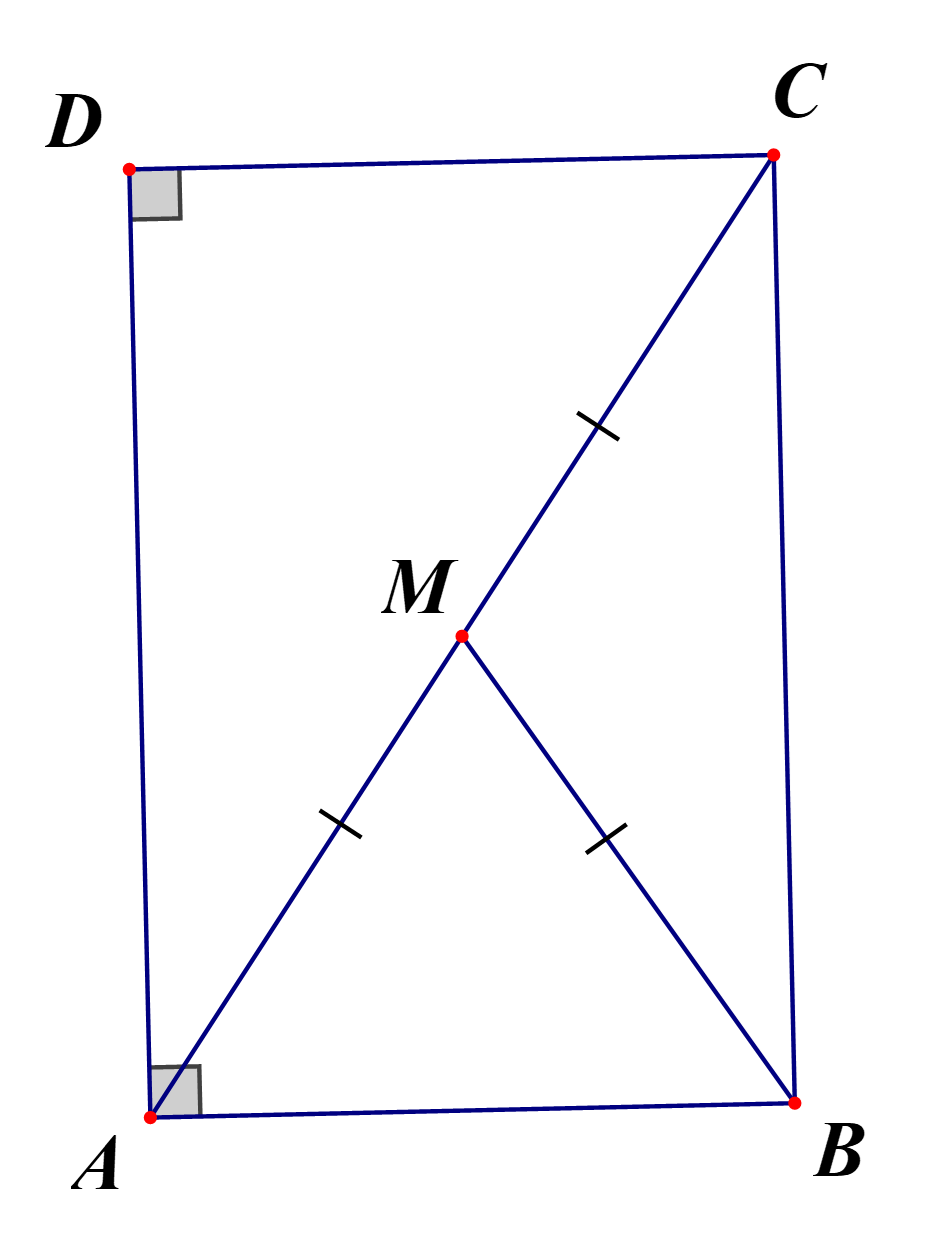
Xét $\Delta ABC$ có $BM$ là đường trung tuyến ứng với cạnh $AC$ mà $BM = \dfrac{1}{2}AC$ suy ra $\Delta ABC$ vuông tại $B$.
Tứ giác $ABCD$ có $\widehat{A}=\widehat{D}=\widehat{B}={{90}^{\circ}}$
Suy ra tứ giác $ABCD$ là hình chữ nhật.
Cho tam giác $ABC$ có đường cao $AI$. Từ $A$ kẻ tia $Ax$ vuông góc với $AC$, từ $B$ kẻ tia $By$ song song với $AC$. Gọi $M$ là giao điểm của tia $Ax$ và tia $By$. Nối $M$ với trung điểm $P$ của $AB$, đường $MP$ cắt $AC$ tại $Q$ và $BQ$ cắt $AI$ tại $H$.
a) Tứ giác $AMBQ$ là hình gì?
b) Chứng minh tam giác $PIQ$ cân.
Hướng dẫn giải:
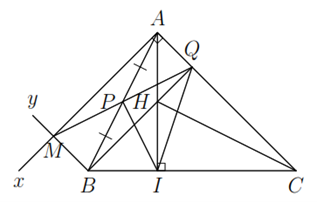
a) Ta có: $Ax\bot AC$ và $By$ // $AC$
Suy ra $Ax\bot By$ $\Rightarrow \widehat{AMB}=90^\circ$.
Xét $\Delta MAQ$ và $\Delta QBM$ có
$\widehat{MQA}=\widehat{BMQ}$ (so le trong);
$MQ$ là cạnh chung;
$\widehat{AMQ}=\widehat{BQM}$ ($Ax$ // $QB$).
Suy ra $\Delta MAQ= \Delta QBM$ (g-c-g)
Suy ra $\widehat{MBQ}=\widehat{MAQ}=90^\circ$ (2 góc tương ứng)
Xét tứ giác $AMBQ$ có: $\widehat{QAM}=\widehat{AMB}=\widehat{MBQ}=90^\circ$
Suy ra tứ giác $AMBQ$ là hình chữ nhật.
b) Do tứ giác $AMBQ$ là hình chữ nhật.
Mà $ P$ là trung điểm AB$ nên $PQ=\dfrac{1}{2}AB$ (1)
Xét $\Delta AIB$ vuông tại $I$ và có $IP$ là đường trung tuyến.
Suy ra $IP=\dfrac{1}{2}AB$ (2)
Từ (1) và (2) $\Rightarrow QP=IP\Rightarrow \Delta PQI$ cân tại $P$.
