Bài tập tự luận: Đường trung bình của tam giác SVIP

Hướng dẫn giải:

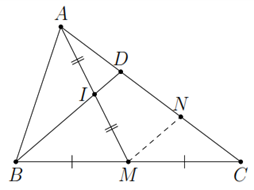
a) Kẻ $MN$ // $ BD$, $N\in AC$.

$MN$ là đường trung bình trong $\triangle CBD$

Suy ra $N$ là trung điểm của $CD$ (1).

$IN$ là đường trung bình trong $\triangle AMN$

Suy ra $D$ là trung điểm của $AN$ (2).

Từ (1) và (2) suy ra $AD=\dfrac{1}{2}DC$.

b) Có $ID=\dfrac{1}{2}MN$; $MN=\dfrac{1}{2}BD$, nên $BD=ID$.

Hướng dẫn giải:

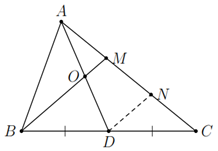
a) Qua $D$ vẽ một đường thẳng song song với $BM$ cắt $AC$ tại $N$.

Xét $\Delta MBC$ có $DB=DC$ và $DN$ // $BM$ nên $MN=NC=\dfrac{1}{2}MC$ (định lí đường trung bình của tam giác).

Mặt khác $AM=\dfrac{1}{2}MC$, do đó $AM=MN=\dfrac{1}{2}MC$.

Xét $\Delta AND$ có $AM=MN$ và $BM$ // $DN$ nên $OA=OD$ hay $O$ là trung điểm của $AD$.

b) Xét $\Delta AND$ có $OM$ là đường trung bình nên $OM=\dfrac{1}{2}DN$. (1)

Xét $\Delta MBC$ có $DN$ là đường trung bình nên $DN=\dfrac{1}{2}BM$. (2)

Từ (1) và (2) suy ra $OM=\dfrac{1}{4}BM$.

Hướng dẫn giải:

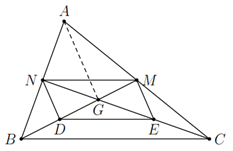
a) Vì $BM$, $CN$ là các đường trung tuyến của $\Delta ABC$ nên $MA=MC$, $NA=NB$.

Do đó $MN$ là đường trung bình của $\Delta ABC$, suy ra $MN$ // $ BC$. (1)

Ta có $DE$ là đường trung bình của $\Delta GBC$ nên $DE$ // $ BC$.  (2)

Từ (1) và (2) suy ra $MN$ // $ DE$.

b) Xét $\Delta ABG$, ta có $ND$ là đường trung bình.

Xét $\Delta ACG$, ta có $ME$ là đường trung bình.

Do đó $ND$ // $ AG$, $ME$ // $ AG$.

Suy ra $ND$ // $ ME$.

Hướng dẫn giải:

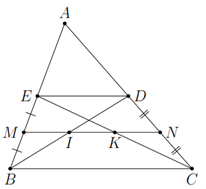
Xét $\Delta BED$ có $\left\{ \begin{aligned} & MI\, \text{//} \, ED \\ & ME=BM \\ \end{aligned} \right.$ suy ra $ ID=IB$.

Xét $\Delta CED$ có $\left\{ \begin{aligned} & NK\, \text{//} \, ED \\ & NC=ND \\ \end{aligned} \right.$ suy ra $KE=KC$.

Suy ra $MI=\dfrac{1}{2}ED$; $NK=\dfrac{1}{2}ED$; $ED=\dfrac{1}{2}BC$.

$IK=MK-MI=\dfrac{1}{2}BC-\dfrac{1}{2}DE=DE-\dfrac{1}{2}DE=\dfrac{1}{2}DE$.

Vậy $MI=IK=KN$.