Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Bài tập tính chất hai tiếp tuyến cùng xuất phát từ một điểm SVIP
Cho đường tròn $(O)$, điểm $A$ nằm bên ngoài đường tròn. Kẻ các tiếp tuyến $AM$, $AN$ với đường tròn ($M$, $N$ là các tiếp điểm).
a) Chứng minh \(OA\perp MN\).
b) Gọi I là giao điểm của $OA$ với $(O)$. Chứng minh $I$ là tâm đường tròn nội tiếp tam giác $MNA$.
c) Góc $MAN$ bằng bao nhiêu độ để tứ giác $OMIN$ là hình thoi?
Hướng dẫn giải:
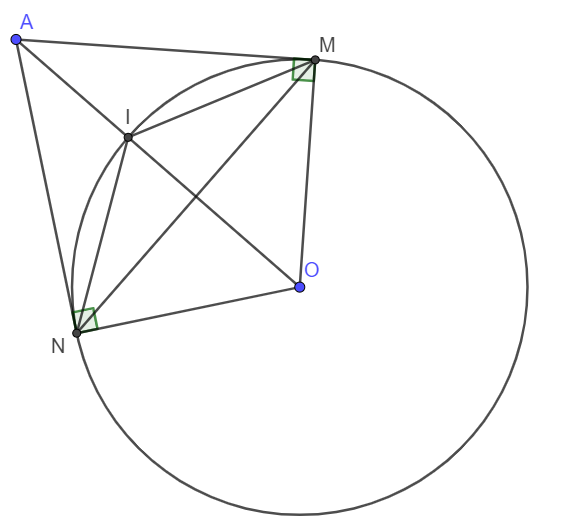
a) Tam giác MAN cân tại A có OA là tia phân giác nên nó cũng trùng với đường cao. Vì vậy \(OA\perp MN\).
b) Do AM, AN là hai tiếp tuyến cùng xuất phát từ một điểm nằm ngoài đường tròn nên AO là phân giác góc \(\widehat{MAN}\) và I là điểm chính giữa của cung MN. Từ đó ta có:
\(\widehat{NMI}=\dfrac{1}{2}sđ\stackrel\frown{NI}=\dfrac{1}{2}sđ\stackrel\frown{MI}=\widehat{IMA}\).
\(\Rightarrow\) IM là phân giác góc \(\widehat{NMA}\).
\(\Rightarrow\) I là tâm đường tròn nội tiếp tam giác MNA.
c) Nếu tứ giác OMIN là hình thoi thì \(OM=ON=MI=IN=R\).
Suy ra các tam giác OMI, ONI là tam giác đều. Vì vậy \(\widehat{MON}=\widehat{MOA}+\widehat{AON}=60^o+60^o=120^o\).
Suy ra \(\widehat{MAN}=180^o-\widehat{MON}=60^o\).
Ngược lại giả sử \(\widehat{MAN}=60^o\). Suy ra \(\widehat{MON}=180^o-\widehat{MAN}=120^o\).
Có OA là tia phân giác của góc MON nên \(\widehat{MOA}=\widehat{AON}=120^o:2=60^o\).
Suy ra các tam giác MOA, AON là tam giác đều hay tứ giác OMIN là hình thoi.
Vậy \(\widehat{MAN}=60^o\) thì tứ giác OMIN là hình thoi.
Cho nửa đường tròn tâm $O$ đường kính $AB$. Gọi $Ax$, $By$ là các tia vuông góc với $AB$ ($Ax$, $By$ và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ $AB$). Gọi $M$ là điểm bất kì thuộc tia $Ax$. Qua $M$ kẻ tiếp tuyến với đường tròn, cắt $By$ ở $N$.
a) Tính số đo góc $MON$.
b) Chứng minh rằng \(AM.BN=R^2\) ($R$ là bán kính của nửa đường tròn).
c) Tìm vị trí điểm $M$ để diện tích hình thang $AMNB$ nhỏ nhất.
Hướng dẫn giải:

a) Gọi I là tiếp điểm của tiếp tuyến MN với nửa đường tròn (O).
Theo tính chất của tiếp tuyến cắt nhau, ta có:\(\widehat{MOA}=\widehat{MOI},\widehat{ION}=\widehat{NOB}\).
Vì vậy \(\widehat{MON}=\widehat{MOI}+\widehat{ION}=\dfrac{1}{2}\left(\widehat{AOI}+\widehat{ION}\right)=90^o\).
b) Theo tính chất của hai tiếp tuyến cắt nhau, ta có: \(MA=MI,IN=NB\).
Vì vậy \(AM.BN=MI.NI\).
Theo hệ thức lượng trong tam giác vuông: \(OI^2=MI.IN\).
Vì vậy \(AM.BN=MI.NI=OI^2=R^2\).
c) Ta chứng minh được \(\Delta AMO=\Delta IMO\), \(\Delta INO=\Delta BNO\).
Diện tích hình thang AMNB bằng:
\(S_{\Delta AMO}+S_{\Delta IMO}+S_{\Delta INO}+S_{\Delta BNO}\).
\(=2S_{\Delta MIO}+2S_{\Delta ION}\) \(=2\left(S_{\Delta MIO}+S_{\Delta ION}\right)\)\(=2S_{\Delta MON}\).
Suy ra diện tích hình thang AMNB nhỏ nhất khi diện tích tam giác MON nhỏ nhất.
\(S_{\Delta MON}=\dfrac{1}{2}OI.MN=\dfrac{1}{2}.R.MN\).
Vậy để diện tích MON nhỏ nhất thì MN có độ dài nhỏ nhất.
\(MN=MI+IN\).
Áp dụng bất đẳng thức Cô-si ta có: \(\left(MI+IN\right)^2\ge4\text{ }MI.IN=4R^2\).
Suy ra \(\min_{MI+IN}=2R\).
Dấu bằng xảy ra khi và chỉ khi: \(MI=IN=R\).
Suy ra \(AM=MI=IN=NB\)\(=R\).
Vậy điểm M thuộc tia Ax sao cho \(AM=R\) thì hình thang AMNB có diện tích nhỏ nhất.
Cho tam giác $ABC$ vuông tại $A$. Đường tròn $(O)$ nội tiếp tam giác $ABC$ tiếp xúc với $AB$, $AC$ lần lượt tại $D$ và $E$.
a) Tứ giác $ADOE$ là hình gì?
b) Chứng minh \(S=p.r\) ($p$ là nửa chu vi tam giác $ABC$, $r$ là bán kính đường tròn nội tiếp).
b) Tính bán kính của đường tròn $(O)$ biết $AB = 6cm$, $AC = 8cm$.
Hướng dẫn giải:

a) Dễ thấy tứ giác AEOD là hình chữ nhật (tứ giác có 3 góc vuông).
Mà OD = OE ( cùng bằng bán kính đường tròn nội tiếp tam giác ABC).
Nên tứ giác AEOD là hình vuông.
b) Gọi H là chân đường vuông góc kẻ từ O xuống BC.
Có \(S_{\Delta ABC}=S_{\Delta OAB}+S_{\Delta OBC}+S_{\Delta OAC}\)
\(=\dfrac{1}{2}OD.AB+\dfrac{1}{2}OE.AC+\dfrac{1}{2}OH.BC\)
\(=\dfrac{1}{2}r.\left(AB+AC+BC\right)\)
\(=\dfrac{1}{2}pr\) ($p$ là chu vi của tam giác $ABC$, $r$ là bán kính đường tròn nội tiếp).
c) Áp dụng định lý Pi-ta-go ta có: \(BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\).
Diện tích tam giác ABC là: \(\dfrac{1}{2}AB.AC=\dfrac{1}{2}.6.8=24\left(cm^2\right)\).
Chu vi tam giác ABC là: \(6+8+10=24\left(cm\right)\).
Suy ra: \(24=\dfrac{1}{2}.24.r\Leftrightarrow r=2\left(cm\right)\).
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$. Vẽ đường tròn tâm $A$, bán kính $AH$. Kẻ các tiếp tuyến $BD$, $CE$ với đường tròn ($D$, $E$ là các tiếp điểm khác $H$). Chứng minh rằng:
a) Ba điểm $D$, $A$, $E$ thẳng hàng.
b) $DE$ tiếp xúc với đường tròn đường kính $BC$.
Hướng dẫn giải:

a) Theo tính chất của hai của hai tiếp tuyến cắt nhau, ta có:
\(\widehat{DAB}=\widehat{BAH}\); \(\widehat{HAC}=\widehat{CAE}\).
Suy ra: \(\widehat{DAE}=\widehat{DAB}+\widehat{BAH}+\widehat{HAC}+\widehat{CAE}\)\(=2\widehat{BAH}+2\widehat{HAC}\)\(=2\widehat{BAC}=180^o\).
Do \(\widehat{DAE}=180^o\) nên DE là đường kính, suy ra D, E, A thẳng hàng.
b) Theo câu a: DE là đường kính đường tròn tâm A.
Có \(BD\perp DE,CE\perp DE\). Suy ra BD//CE.
Gọi O là trung điểm BC.
Vậy tứ giác BDEC là hình thang. Do O và A lần lượt là trung điểm của BC, DE nên OA là đường trung bình của hình thang BDEC.
Suy ra \(OA\perp DE\) mà \(OA=\dfrac{BC}{2}\) nên OA là bán kính của đường tròn đường kính BC.
Thế thì $DE$ tiếp xúc với đường tròn đường kính $BC$.
Cho tam giác $ABC$ cân tại $A$ nội tiếp đường tròn $(O)$. Các tiếp tuyến của đường tròn vẽ từ $A$ và $C$ cắt nhau tại $M$. Trên tia $AM$ lấy điểm $D$ sao cho $AD = BC$. Chứng minh rằng:
a) Tứ giác $ABCD$ là hình bình hành.
b) Ba đường thẳng $AC$, $BD$, $OM$ đồng quy.
Hướng dẫn giải:

a) Có:
\(\widehat{MAC}=\dfrac{1}{2}sđ\stackrel\frown{AC}\), \(\widehat{ACB}=\dfrac{1}{2}sđ\stackrel\frown{AB}.\)
Mà \(sđ\stackrel\frown{AB}=sđ\stackrel\frown{AC}\)
Vì vậy AD = BC và AD//BC nên tứ giác ABCD là hình bình hành.
b) Theo tứ giác ABCD là hình thành nên BD và AC cắt nhau tại trung điểm của mỗi đường.
Theo tính chất của hai tiếp tuyến cắt nhau thì \(MA=MC\) và OM là tia phân giác góc AMC.
AM = MC nên tam giác AMC cân tại M và MO là tia phân giác của tam giác AMC nên OM cũng đi qua trung điểm của AC.
Suy ra ba đường thẳng AC, BD, OM đồng quy.
Trên các cạnh BC và CD của hình vuông ABCD, lấy các điểm M và N sao cho chu vi tam giác MNC bằng nửa chu vi hình vuông. Tìm số đo góc MAN.
Hướng dẫn giải:
Gọi chu vi tam giác CMN bằng p.
Tìm ý tưởng: p = BC + CD, hệ thức này gợi cho ta đến tính chất của đường tròn bàng tiếp (xem bài 2). Ở đây là đường tròn bàng tiếp góc C của ΔCMN.
Gọi B’, D’ lần lượt là các tiếp điểm của đường tròn bàng tiếp góc C của ΔCMN với đường kéo dài cạnh CM, CN.
Ta đã có, CB’ = CD’ = $\frac{p}{2}$ = CB = CD $\Rightarrow$ B’ $\equiv$ B và D $\equiv$ D’. Do đó, tâm đường tròn bàng tiếp góc C của tam giác CMN là điểm A.
Từ đó, $\widehat{MAN}=\widehat{MAC}+\widehat{NAC}=\frac{1}{2}\left(\widehat{BAC}+\widehat{DAC}\right)={45}^\circ$.
Cho một điểm A ở ngoài đường tròn (O). Kẻ hai cát tuyến AMN và APQ tới đường tròn sao cho MN > PQ. Dựng đường tròn (O ; OA). Kẻ hai dây AD và AF của đường tròn lớn tiếp xúc với đường tròn nhỏ tại B và C. Cát tuyến AMN và cát tuyến APQ cắt đường tròn lớn ở E và H.
a) Chứng minh AD = AF;
b) Chứng minh AE > AH;
c) Chứng minh bốn điểm A, B, O, C cùng nằm trên một đường tròn;
d) So sánh $\widehat{OAE}$ và $\widehat{OAH}$.
Hướng dẫn giải:
a) AD và AF cách đều tâm O nên chúng bằng nhau.
b) Kẻ OI $\bot$ MN, OK $\bot$ PQ.
Trong đường tròn nhỏ, ta có: MN > PQ $\Rightarrow$ OI < OK.
(Dây lớn hơn thì gần tâm hơn)
Trong đường tròn lớn, OI < OK $\Rightarrow$ AE > AH.
(Dây gần tâm hơn thì lớn hơn)
c) A, B, O, C cách đều trung điểm AO.
d) $OI < OK\Rightarrow\frac{OI}{OA}<\frac{OK}{OA}$
$\Rightarrow \sin{\widehat{OAI}}< \sin{\widehat{OAK}} \Rightarrow \widehat{OAI}<\widehat{OAK} \Rightarrow \widehat{OAE}<\widehat{OAH}.$

