Bài học cùng chủ đề
- Bài 1: Xét tính đơn điệu của hàm số trên một khoảng xác định (P1)
- Bài 1: Xét tính đơn điệu của hàm số trên một khoảng xác định
- Bài 1: Xét tính đơn điệu của hàm số trên một khoảng xác định (P2)
- Bài 2: Các bài toán biến thiên chứa tham số (P1)
- Bài 2: Các bài toán biến thiên chứa tham số (P2)
- Bài 2: Các bài toán biến thiên chứa tham số
- Bài 3: Các bài toán biến thiên chứa hàm hợp
- Bài 3: Các bài toán biến thiên chứa hàm hợp
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Bài 2: Các bài toán biến thiên chứa tham số (P2) SVIP

Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Cho f′(x)=ax2+bx+c , f′(x)≤0 ∀x∈R⇔ a
- <
- >
- >=
- <=
Cho g(x)=3x2+6x, đạo hàm g′(x)=0 có nghiệm
Cho hàm số g(x)=3x2+6x có bảng biến thiên như hình dưới:
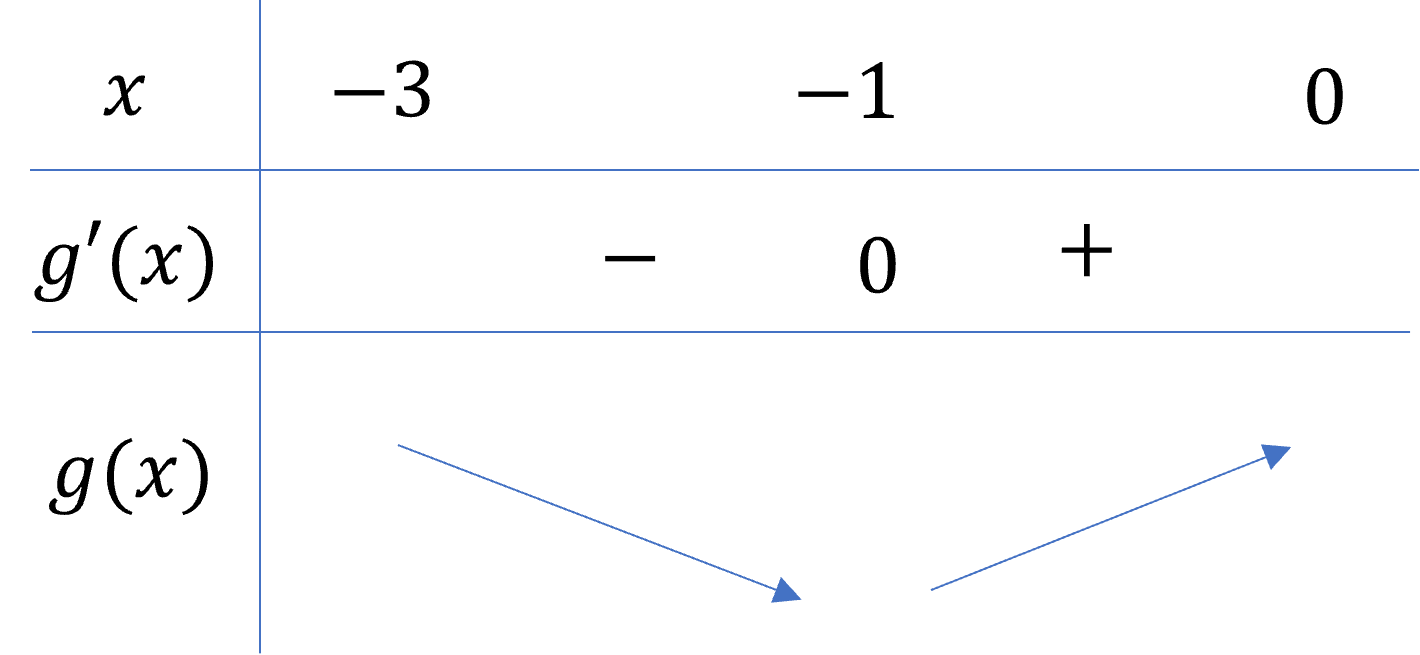
Với x∈(−3;0) , giá trị nhỏ nhất của hàm số g(x) là
- -9
- -3
- 3
- -1
- 0
- -3
m≤6x−63x2−6x+5=g(x) ∀x∈(2;+∞) ⇔
Cho hàm số y′=x2−(2m−1)x+m2−m−2 có hai nghiệm [x=m−2x=m+1 được biểu diễn như hình dưới:

Trên khoảng (m+1;+∞), y′
- >
- <
Cho hàm số y′=−x2+2(m+2)x−m(m−3).
Xét trường hợp Δ≤0 ⇒y′
- <
- >
Cho y=ax2+bx+c có hai nghiệm phân biệt x1,x2, theo định lí Viet ta có:
x1+x2=
x1.x2=
(Kéo thả hoặc click vào để điền)
Tập xác định của hhàm số y=x+mx+2 là
Cho y′=x2−(2m−1)x+m2−m+2=0 có 2 nghiệm [x=m−2x=m+1. Hàm số y=f(x) nghịch biến trên khoảng (1;2) khi
Hàm số y=x+mx+2 đồng biến trên khoảng (−∞;−5) khi và chỉ khi
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- Xin chào mừng các em quay sửa lại về
- khóa học Toán lớp 12 của chàng
- webcode.vn và bài học ngày hôm nay thì
- chúng ta sẽ tiếp tục tìm hiểu chuyên đề
- tính đơn điệu của hàm số trong cái video
- trước thì ta đã tìm hiểu trong dạng hụt
- của bài 2 các bài toán Yến Thiên có điều
- kiện và bây giờ thì chúng ta sẽ tìm hiểu
- cái dạng toán còn lại là dạng toàn thứ 2
- tìm m để hàm số đơn điệu trên một khoảnh
- Thế thì để giải được những cái bài toán
- thuộc dạng toán này thì chúng ta sẽ thực
- hiện qua một số bước
- Bước đầu tiên là tìm được xác định và
- tìm đạo hàm hàm số đã cho bước thứ 2 thì
- tùy vào cái yêu cầu của đề bài mà chúng
- ta sẽ đưa ra được những cái điều kiện
- của y phẩy Thế thì để hàm số FX đồng
- biến trên khoảng từ a đến b thì tương
- đương với phẩm phải lớn hơn hoặc bằng 0
- với mọi x thuộc khoảng AB và chúng ta
- chú ý là dấu bằng về xảy ra tại hữu hạn
- nghiệp và tương tự để hàm số y bằng FX
- nghịch biến a a đến b thì y phẩy nhỏ thu
- hoặc bằng 0 với mọi x thuộc khoảng AB và
- dấu bằng cũng phải xảy ra tại hữu hạn
- điểm
- bước thứ ba để tìm được cái điều kiện
- của tham số m thì chúng ta sẽ phải sử
- dụng một số phương pháp nào sau đây thì
- cô nêu ra hai cái phương pháp phổ biến
- nó đầu tiên là câu lực tham số m thứ hai
- là ta sử dụng dấu của tam thức bậc 2 kết
- hợp với định lý Viet
- Thế thì cưới Phương pháp đầu tiên có lực
- tham số m nghĩa là ta chuyển mở sang một
- ví và cái hàm số chữ X ra một ví khi đó
- ta được là m nhỏ thuộc bằng GX hoặc là
- mười lớn hơn hoặc bằng GX với trường hợp
- m nhỏ thu bằng GX thì tương đương với M
- nhỏ hơn hoặc bằng pin của GX nghĩa là
- giá trị nhỏ nhất của gợi ý gửi mọi thử
- khoảng A đến B và tương tự thì mời lớn
- hơn hoặc bằng GX khi và chỉ khi M lớn
- hơn hoặc bằng giá trị lớn nhất của X với
- mọi x thường khoảng a đến ạ sau đỏ thì
- chúng ta Lập bảng biến thiên của X và
- tìm giá trị nhỏ nhất hoặc là lớn nhất
- của GX gửi ít được khoảng từ A đến B
- về với trường hợp mà bài toán mà ta
- không thể có được tham số mừng thì chúng
- ta sẽ sử dụng phương pháp thứ hai
- dấu của tam thức bậc 2 kết hợp với định
- lý Viet
- dấu của tam thức bậc hai SX có dạng là
- ax bình phương cộng bx cộng c thì FX vẽ
- lớn hơn hoặc bằng 0 với mọi x thuộc R
- khi và chỉ khi là a lớn hơn 0 và Delta
- nhỏ thuộc bằng không tương tự là SX nhỏ
- thu bằng 0 với mọi x thuộc R khi và chỉ
- khi anh ngỏ Thư không và Delta nhỏ thu
- bằng không
- tiếp theo là định lý vị ép vậy với những
- cái đang thức mà có hai nghiệm phân biệt
- x1 x2
- thì ta có tổng của X1 và X2 = -3 trên a
- và tích X1 nhân và x2 = C trên a và bước
- cuối cùng là chúng ta kết luận
- và bây giờ vào sử dụng những cái phương
- pháp hay là quy tắc mà cô vừa nêu ra thì
- chúng ta sẽ cùng nhau thực hiện một số
- ví dụ bài tập ví dụ đầu tiên
- tìm các giá trị thực của tham số m để
- hàm số đã cho nghịch biến trên khoảng từ
- thứ Ba đến không
- thấy bước đầu tiên và tìm được xác định
- và đạo hàm hàm số này có d = r và đạo
- hàm If face thì bằng thì ba những x bình
- phương trừ 6 x + m
- vậy hàm số trên nghịch biến trên khoảng
- từ thứ Ba đến không khi vào thì khi lại
- phẩm nhỏ chưa bằng 0 với mọi x thuộc
- khoảng từ 3 đến không Ừ cái này tương
- đương gửi cho gãy bình phương chỉ rõ Ít
- + mở nhỏ thôi bằng không và ít cũng
- thuộc khoảng từ 3 đến không
- Bây giờ thì chúng ta sẽ có lập tham số
- mở chuyển mời sang một ghế đã được mơ
- nhỏ Thượng = 3 x bình phương cộng 6X và
- đặt cái đa thức 3 x bình phương cộng 6X
- bằng RX thì ta có làm mờ phải nhỏ thuốc
- bằng min của hợp X với x thuộc khoảng từ
- 3 đến không
- phải đến đây thì chúng ta Lập bảng biến
- thiên của hợp X
- ta có này thích thì cạnh thì ba đến
- không Bây giờ ta phải tìm nghiệm của
- phương trình rvx vừa phải kích thì sẽ
- bằng
- 6 x + 6 g và x bằng 0 khi và chỉ khi X =
- -1 vậy ta Điền - 1 vào đây hết xấu của
- phải X thì ta nhận thấy là tao gửi về X
- có a = 6 Cho a
- lớn hơn 0
- Nhưng ta điền được ở đây mang dấu xương
- quan nghĩ rằng truyền một thìa Vĩ đổi
- dấu thành âm bây giờ thì chúng ta Hoàn
- thành bảng biến thiên của x bằng cách
- điền các giá trị của x và y bằng trừ 1 x
- = 0 và x = -3
- Thế thì tại X = -1 to Thay vào GX sẽ =
- -3 hãy toàn không chứa x = 0 và tại X =
- -3 thì thử x = 9 vậy là người x thuộc
- khoảng từ 3 đến không min của x = -3 vậy
- dựa vào bảng biến thiên thì ta có làm mờ
- nhỏ thuộc = 3 x bình phương cộng 6X khi
- và chỉ khi làm người nhà thu bằng chứa
- bạn vậy ta kết luận là các giá trị của
- người cần tìm là mờ nhà thuốc bằng thứ
- ba
- ví dụ tiếp theo thì dụng 1.2 I anh có
- tất cả bao nhiêu giá trị nguyên dương là
- chủ yếu là nguyên dương của tham số m để
- hàm số này đồng biến trên khoảng thứ hai
- đến dương vô cùng thứ tự về các ví dụ
- trước thì ta có tập xác định hàm số này
- là liệu bằng R phẩy = 3 x bình phương -
- xấu nhưng mà cộng 1 nhân với x + 6 m + 5
- cá có hàm số trên đồng biến trên khoảng
- từ 2 đến dương vô cùng khi và chỉ khi đi
- phẩy lấy mà không với mọi x thuộc khoảng
- từ 2 đến dương vô cùng
- từ ngày tương đương gửi là 3 x bình
- phương - xấu như 1 cộng 1 nhân với x + 6
- m + 5 lớn hơn và không với mọi cực
- khoảng thứ hai đến dương vô cùng
- mà nhóm những cái giá trị mà chiếu m lại
- thì ta được là 6m nhân với x trừ 1 nhỏ
- thuộc bằng bãi bình phương trừ 6 x + 5
- đến đây ta nhận thấy những là do ích lớn
- hơn hay nên là ít - 1 sẽ lớn hơn không
- vì
- vậy ta chia cả hai vế cho Sáu nhân vĩ -
- 1 ta được làm mờ nhỏ thuộc = 3 x bình
- phương trừ 6 x + 5 trên 6 x trừ 6 và đặt
- cái đa thức này bằng
- GX đây rồi ta tính đạo hàm g7x sẽ bằng
- 18x Phương - 36 x + 6 trên 6 X6 tất cả
- bình phương
- và bây giờ ta Lập bảng biến thiên của
- hàm số GX ta nhận thấy yếu là với ích
- chạy thứ 2 đến dương vô cùng thì vừa
- phải x sẽ lớn hơn không bịt hoàn thành
- được bảng biến thiên của gợi ích Hãy
- bằng hai thì gửi ít sẽ bằng 5/6 vệ
- nguyên của GX là 5/6 dựa vào bảng biến
- thiên thì ta có là mơ nhỏ tự bằng 3 thức
- GX khi vào thì khi làm ở những bằng 5/6
- do đầy Yêu cầu tìm các giá trị nguyên
- dương của tham số m nên K kết luận là
- không gọi giá trị nào của m thỏa mãn A
- ạ
- Bây giờ thì chúng ta cùng bước sang nhìn
- dụng tiếp theo ví dụ 1.3 có tất cả bao
- nhiêu giá trị nguyên của tham số m để
- hàm số trên nghịch biến trên khoảng từ 1
- đến 2
- Thế thì tương tự với những bài trước thì
- bây giờ chúng ta tìm tập xác định hàm số
- này có d = r tiếp theo đạo hàm khi phẩy
- = x bình phương - 20 - 1 nhân x cộng với
- M bình trừ 10 thứ hai
- và để hàm số trên nghịch biến trên
- khoảng từ 1 đến 2 thì y phẩy phải nhiều
- từ bằng 0 với mọi x thuộc khoảng một đến
- hai từ này tương đương với x bình phương
- - 20 - 1 x x cộng với M bình trừ m - 2
- nhỏ thu bằng 0 và đến B ta nhận thấy là
- ta không thể có hợp được tham số m vì
- vậy lá bây giờ ta phải tìm tên ta ta có
- đem ta thì bằng hai người chuyển một
- mình Phương chỉ bốn nhân với M bình trừ
- 1 trừ 2 nên tao bằng chính lớn hơn không
- Nghĩa là y phẩy = 0 có hai nghiệm phân
- biệt
- cho người ta tí nữa X1 thì = m + 1 x 2
- thì bằng 10 - hai tụi bây giờ ta lập
- bảng xét dấu của y phẩy
- sắp xếp nghiệm 10 - 2 thì nhỏ hơn nhiệm
- mời cộng một
- tiếp theo là điền dấu thế tự do y Face
- chị phải có hệ số a ở đây
- anh bằng một
- đời hơn không nên ta điện được xấu của
- khoảng này là dấu dương vậy đi qua các
- nhiệm phân biệt thì phải đổi dấu thành
- âm và dương vẫn ta có khi phải nhỏ thu
- bằng 0 với mọi x thuộc khoảng 1 đến 2
- khi và chỉ khi là m - 2 nhỏ thôi bằng
- tích nhỏ hơn = m + 1
- điều này tương đương với 10 - 2 thì nhỏ
- thu bằng một nhỏ thu hay nhỏ thu = m + 1
- do x thuộc khoảng từ 1 đến 2 vậy chuyển
- về ta có một nhỏ thu bằng mờ nhà thu
- bằng 3
- mà đề bài Yêu cầu tìm giá trị nguyên của
- tham số m vì vậy là ta nhận được 3 giá
- trị m bằng 1 m bằng hai hoặc là mười
- bằng 3 thỏa mãn điều kiện Đề bài một ví
- dụ thứ tư Tìm tất cả các giá trị thực
- của tham số m để cái hàm số này nghịch
- biến trên khoảng từ một điểm Sương Vô
- Cùng
- được xác định của số này
- - face thì bằng trừ x bình phương cộng 2
- x bình trừ 2x - m nhân với 10 - 3 có để
- hàm số trên nghịch biến trên khoảng từ 1
- đến dương vô cùng khi phải nhỏ thuộc
- bằng 0 với mọi x thuộc khoảng một đến
- dương vô cùng
- tương đương với chị ý bình phương cộng 2
- x bình trừ 2x - m nhân với 10 - 3 nhỏ
- thu bằng 0
- và tương tự với bài toán trước thì ta
- nhận thế là ta cũng không thể cô lập
- được tham số m đã tính delta ở đây thì
- ta có thể tính nên ta phẩy = 4 - mờ
- mà ta xét trường hợp một người Ý trường
- hợp bên ta phải nhỏ thôi bằng không
- Nghĩa là 4 - Mở nhà thuốc bằng không mở
- lớn hơn hoặc bằng 4 vậy do a của y phẩy
- = -1 nhỏ thu không vậy nên lá ta thích
- hợp a nhỏ tôi không và denta phẩy nhà
- thuốc bằng không vì vậy là y phẩy sẽ nhỏ
- thuộc bằng 0 với mọi x thuộc R
- anh cũng nhỏ thường không với ít thuộc
- một đến dương vô cùng vì vậy là mờ lớn
- hơn bằng bốn thỏa mãn yêu cầu của bài
- toán
- bây giờ chúng ta cũng xét xanh để trường
- hợp thứ 2 đó là trường hợp anten lớn hơn
- không Nghĩa là mở nhỏ chưa bốn khi đó
- thì phải sẽ có 2 nghiệm phân biệt là X1
- nhỏ hơn X2 và ta lập bảng xét dấu của y
- phẩy phẩy phẩy có AA = -1 nghĩa là anh
- nhỏ thuốc không nên xấu có khoảng này sẽ
- là dư âm và khi đi qua các nghiệm phân
- biệt khi phải đổi dấu từ âm sang dương
- và Thùy Dương tâm
- vợ yêu cầu đề bài
- là tìm m để hàm số nghịch biến trên
- khoảng từ 1 đến dương vô cùng ta nhận
- thấy khoảng này mang dấu âm bằng này
- cũng mang đầu âm
- nhưng hàm số nghịch biến từ 1 đến dương
- vô cùng nên một sẽ thuộc cái đoạn này từ
- X2 đến dương vô cùng
- điều này có nghĩa là ích một nhỏ thôi X2
- và nhỏ thu bằng 1 ex1 - 1 nhỏ thôi ích 2
- - 1 và nhỏ đi bằng không
- Bây giờ ta lấy tích cổ tích 1 - 1 và ít
- 2 - 1 thì phải lớn hơn 0 và tổng của X1
- - 1 + x 2 - 1 thì phải nhỏ thuốc không
- và biến đổi về dạng tổng tích ta còn họp
- 1 unit 2 - x1 + x2 + một lớn = 0 và X1 +
- X2 - 2 nhỏ cô không đến đây thì chúng ta
- áp dụng các định lý Viet x1 + x2 thì
- bằng trừ B trên a ta có ai phẩy ở đây
- thì bên A sẽ là bằng hai nhân với M - 2
- và X1 X2 bằng C trên A thì sẽ bằng m
- nhân với M - 3 dậy thay vào sao ta có
- sao tương đương với mơ nhân với 10 - 3 -
- 2 nhân với 10 - 2 cộng 1 lớn hơn hoặc
- bằng 0 và 2 nhân với 10 - 2 - 2 nhỏ thu
- không
- giải thế hệ phương trình này ra thì ta
- được là nhờ lớn hơn hoặc a + căn 5 xin
- hai hoặc m nhỏ bằng 5 trừ căn 5 trên 2
- kết hợp với mở nhỏ thứ 3 tập cuối cùng
- người ta nhận được tiền nhờ nhà trong
- bằng 5 - gian 592
- vậy kết hợp hai trường hợp với trường
- hợp 1 là Delta nhỏ thu bằng 0 và trường
- hợp hay là Delta lớn hơn Không thì ta
- được làm mờ sẽ lớn hơn hoặc bằng 4 hoặc
- là nhờ nhỏ thu bằng 5 trừ căn 5 trên hai
- sẽ kết thúc cái ví dụ 1.4 ở đây bước
- sang ví dụ cuối cùng ví dụ 1.5
- Câu hỏi đặt ra là có bao nhiêu giá trị
- nguyên của tham số m để hàm số y bằng x
- cộng 2 trên x cộng m đồng biến trên
- khoảng từ âm vô cùng đến C5
- bài toán này thì có khác những cái bài
- toán trước một tí đó là cái Hàn mình cho
- không phải là hàm đa thức nữa mà là hàm
- phân thức bậc nhất trên bậc nhất
- Tuy nhiên là cách làm của chúng ta cũng
- hoàn toàn tương tự thôi đầu tiên tập xác
- định hàm số ở đây là bằng R - - M nghĩa
- là ít người khác trời nhờ thứ hai đạo
- hàm If thì = m - 2 trên x cộng 1 tất cả
- bình phương Vậy thì hàm số trên đồng
- biến trên khoảng từ âm vô cùng đến - 5
- khi phẩy phải lớn hơn 0 với mọi x thuộc
- khoảng từ âm vô cùng đến thứ năm và do
- cái điều kiện xác định của mình là ích
- khác chỉ mờ vì vậy là trình mới cũng sẽ
- không thuộc cái khoảng từ âm vô cùng đến
- thứ năm
- đi phẩy lớn hơn Không thì khi và chỉ khi
- làm mờ - 2 lớn hơn 0 và trừ m không
- thuộc khoảng từ âm vô cùng đến - 5 định
- nghĩa là trường M lớn hơn hoặc bằng - 5
- điều này tương đương với hai nhỏ thương
- mở nhỏ thu hằng năm vậy ta kết luận là
- có 3 giá trị nguyên của nhờ thỏa mãn là
- mở bằng 3 = 4 hoặc là bằng 5 vậy bài học
- của chúng ta hôm nay kết thúc tại đây
- Cảm ơn các em đã chú ý lắng nghe và hẹn
- gặp lại các em trong các kế bài giảng
- tiếp theo
Bạn có thể đăng câu hỏi về bài học này ở đây
