

Nguyễn Minh Kiên
Giới thiệu về bản thân




































Gọi \(D\) là giao điểm của \(A G\) và \(B C \Rightarrow D B = D C\).
Ta có \(B G = \frac{2}{3} B E\); \(C G = \frac{2}{3} C F\) (tính chất trọng tâm).
Vì \(B E = C F\) nên \(B G = C G \Rightarrow \triangle B C G\) cân tại \(G\)
\(\Rightarrow \hat{G C B} = \hat{G B C}\)
Xét \(\triangle B F C\) và \(\triangle C E B\) có \(C F = B E\) (giả thiết);
\(\hat{G C B} = \hat{G B C}\) (chứng minh trên);
\(B C\) là cạnh chung.
Do đó \(\triangle B F C = \triangle C E B\) (c.g.c)
\(\Rightarrow \hat{F B C} = \hat{E C B}\) (hai góc tưong ứng)
\(\Rightarrow \triangle A B C\) cân tại \(A \Rightarrow A B = A C\).
Từ đó suy ra \(\triangle A B D = \triangle A C D\) (c.c.c)
\(\Rightarrow \hat{A D B} = \hat{A D C}\). (hai góc tương ứng)
Mà \(\hat{A D B} + \hat{A D C} = 18 0^{\circ} \Rightarrow \hat{A D B} = \hat{A D C} = 9 0^{\circ} \Rightarrow A D \bot B C\) hay \(A G \bot B C\).
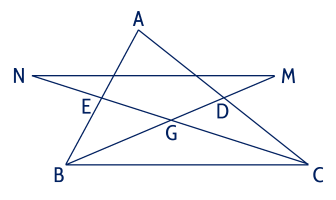
a) Ta có \(D M = D G \Rightarrow G M = 2 G D\).
Ta lại có \(G\) là giao điểm của \(B D\) và \(C E \Rightarrow G\) là trọng tâm của tam giác \(A B C\)
\(\Rightarrow B G = 2 G D\).
Suy ra \(B G = G M\).
Chứng minh tương tự ta được \(C G = G N\).
b) Xét tam giác \(G M N\) và tam giác \(G B C\) có \(G M = G B\) (chứng minh trên);
\(\hat{M G N} = \hat{B G C}\) (hai góc đối đỉnh);
\(G N = G C\) (chứng minh trên).
Do đó \(\triangle G M N = \triangle G B C\) (c.g.c)
\(\Rightarrow M N = B C\) (hai cạnh tương ứng).
Theo chứng minh trên \(\triangle G M N = \triangle G B C \Rightarrow \hat{N M G} = \hat{C B G}\) (hai góc tương ứng).
Mà \(\hat{N M G}\) và \(\hat{C B G}\) ờ vị trí so le trong nên \(M N\) // \(B C\).
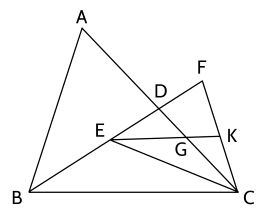
a) Ta có \(B F = 2 B E \Rightarrow B E = E F\).
Mà \(B E = 2 E D\) nên \(E F = 2 E D \Rightarrow D\) là trung điểm của \(E F \Rightarrow C D\) là đường trung tuyến của tam giác \(E F C\).
Vì \(K\) là trung điểm của \(C F\) nên \(E K\) là đường trung tuyến của \(\triangle E F C\).
\(\triangle E F C\) có hai đường trung tuyến \(C D\) và \(E K\) cắt nhau tại \(G\) nên \(G\) là trọng tâm của \(\triangle E F C\).
b) Ta có \(G\) là trọng tâm tam giác \(E F C\) nên \(\frac{G C}{D C} = \frac{2}{3}\) và \(G E = \frac{2}{3} E K\)
\(\Rightarrow G K = \frac{1}{3} E K \Rightarrow G E = 2 G K \Rightarrow \frac{G E}{G K} = 2\).

a) Xét tam giác \(A B D\) có \(C\) là trung điểm của cạnh \(A D \Rightarrow B C\) là trung tuyến của tam giác \(A B D\).
Hơn nữa \(G \in B C\) và \(G B = 2 G C \Rightarrow G B = \frac{2}{3} B C \Rightarrow G\) là trọng tâm tam giác \(A B D\).
Lại có \(A E\) là đường trung tuyến của tam giác \(A B D\) nên \(A , G , E\) thẳng hàng.
b) Ta có \(G\) là trọng tâm tam giác \(A B D \Rightarrow D G\) là đường trung tuyến của tam giác này.
Suy ra \(D G\) đi qua trung điểm của cạnh \(A B\) (điều phài chứng minh).
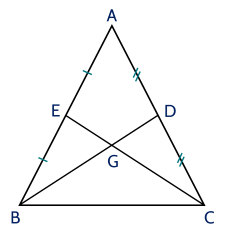
a) Ta có \(\triangle A B C\) cân tại \(A \Rightarrow A B = A C\) mà \(A B = 2 B E\); \(A C = 2 C D\) (vì \(E , D\) theo thứ tự là trung điểm của \(A B\), \(A C \left.\right)\).
Do đó ta có \(2 B E = 2 C D\) hay \(B E = C D\).
Xét \(\triangle B C E\) và \(\triangle C B D\) có \(B E = C D\) (chứng minh trên);
\(\hat{E B C} = \hat{D C B}\);
\(B C\) là cạnh chung.
Do đó \(\triangle B C E = \triangle C B D\) (c.g.c)
\(\Rightarrow C E = B D\) (hai cạnh tương ứng).
b) Ta có \(G\) là trọng tâm tam giác \(A B C\) nên \(B G = \frac{2}{3} B D\) và \(C G = \frac{2}{3} C E\) (tính chất trọng tâm).
Mà \(C E = B D\) (phần a) nên \(\frac{2}{3} C E = \frac{2}{3} B D\) hay \(C G = B G\).
Vậy tam giác \(G B C\) cân tại \(G\).
c) Ta có \(G B = \frac{2}{3} B D \Rightarrow G D = \frac{1}{3} B D \Rightarrow G B = 2 G D \Rightarrow G D = \frac{1}{2} G B\)
Chứng minh tương tự, ta có \(G E = \frac{1}{2} G C\).
Do đó \(G D + G E = \frac{1}{2} G B + \frac{1}{2} G C = \frac{1}{2} \left(\right. G B + G C \left.\right)\).
Mà \(G B + G C > B C\) (trong một tam giác tổng độ dài hai cạnh lớn hơn cạnh còn lại).
Do đó \(G D + G E > \frac{1}{2} B C\) (điều phải chứng minh).
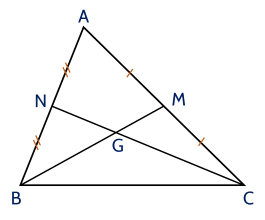
Xét tam giác \(A B C\) có hai đường trung tuyến \(B M\) và \(C N\) cắt nhau tại \(G\).
Suy ra \(G\) là trọng tâm tam giác \(A B C\)
\(\Rightarrow B G = \frac{2}{3} B M\); \(C G = \frac{2}{3} C N\)
\(\Rightarrow B M = \frac{3}{2} B G\); \(C N = \frac{3}{2} C G\).
Do đó ta phải chứng minh \(\frac{3}{2} B G + \frac{3}{2} C G > \frac{3}{2} B C\) hay \(B G + C G > B C\). (1)
Bất đẳng thức (1) luôn đúng vì trong một tam giác tổng độ dài hai cạnh lớn hơn độ dài cạnh còn lại.
Vậy \(B M + C N > \frac{3}{2} B C\). (điều phải chứng minh).
1. Mở bài:
- Dẫn dắt vấn đề. Ví dụ: "Uống nước nhớ nguồn" là truyền thống tốt đẹp của nhân dân ta.
- Nêu vấn đề: Cần tôn trọng đạo lí "Uống nước nhớ nguồn".
2. Thân bài:
- Nêu quan điểm về đạo lí "Uống nước nhớ nguồn":
+ Nghĩa đen: Khi được uống, hưởng dòng nước mát thì hãy nhớ tới nơi khởi đầu cho ta dòng nước đó.
+ Nghĩa bóng: Khi được hưởng thành quả nào đó thì hãy nhớ tới người đã tạo ra thành quả.
- Biểu hiện của việc sống "Uống nước nhớ nguồn":
+ Luôn trân trọng những người quan tâm mình.
+ Luôn ghi nhớ công lao của những người đã giúp đỡ mình.
- Phân tích ý nghĩa của việc sống theo đạo lí "Uống nước nhớ nguồn":
+ Giúp ta không bao giờ hổ thẹn với lòng mình.
+ Giúp ta trở thành người đáng tin cậy, các mối quan hệ cũng vì thế trở nên khăng khít, bền chặt hơn.
+ Một số tấm gương chứng minh cho vẻ đẹp của đạo lí "Uống nước nhớ nguồn":
Phạm Sư Mạnh là học trò nổi tiếng của Chu Văn An, làm quan to nức tiếng triều đình, nhưng khi phạm lỗi vẫn phải quỳ gối tạ tội cùng thầy.
Chử Đồng Tử nhà nghèo, sống cùng cha. Hai cha con chỉ có một chiếc khố chia nhau dùng chung. Đến khi cha mất, trước khi đi, ông có nói với Chử Đồng Tử rằng: “Cha chết đi, con giữ lại cái khố mà che thân, cho thiên hạ khỏi chê cười. Con cứ tang trần cho cha là được.” Ấy vậy nhưng chàng không nỡ tang trần cho cha nên đã dùng chiếc khố duy nhất để an táng cha yên nghỉ.
- Liên hệ với bản thân trong việc rèn luyện sống theo đạo lí "Uống nước nhớ nguồn": bản thân đôi lúc còn sống vô tâm, chưa thật sự biết ghi nhớ công lao của những người đã giúp đỡ mình.
3. Kết bài:
- Khẳng định vai trò của việc sống theo đạo lí "Uống nước nhớ nguồn": đây là lối sống đẹp cần có ở mỗi cá nhân.
- Nêu suy nghĩ về hướng rèn luyện của em:
+ Luôn nói lời "cảm ơn", biết ghi nhớ công lao của cha ông ta, của thầy cô, gia đình, bạn bè,... - những người đã giúp ta có được ngày hôm nay.
+ Không chỉ vậy mà còn luôn chủ động giúp đỡ mọi người xung quanh, lan toả giá trị tích cực của đạo lí "Uống nước nhớ nguồn".
1. Mở bài:
- Dẫn dắt vấn đề cần nghị luận. Ví dụ: Dẫn dắt từ câu tục ngữ: "Người càng vĩ đại thì càng khiêm tốn" (Tục ngữ Hàn Quốc).
- Nêu vấn đề: cần sống khiêm tốn.
2. Thân bài:
- Nêu quan điểm về lối sống khiêm tốn. Ví dụ: Khiêm tốn là tính nhã nhặn, biết sống một cách nhún nhường, luôn hướng về phía trước.
- Nêu biểu hiện của lối sống khiêm tốn:
+ Người khiêm tốn thường tự cho mình là kém cỏi, cần phấn đấu, trau dồi thêm.
+ Người khiêm tốn không bao giờ chấp nhận thành công của cá nhân mình ở thời điểm hiện tại, luôn tìm cách để thành công hơn nữa.
+ Người khiêm tốn không bao giờ hạ thấp người khác để nâng cao mình.
- Phân tích ý nghĩa của sống khiêm tốn:
+ Giúp ta không ngừng phấn đấu, không ngừng học hỏi để vươn lên mỗi ngày.
+ Giúp ta trở thành một người đáng tin cậy, các mối quan hệ vì thế cũng trở nên khăng khít, bền chặt hơn.
+ Một số tấm gương đã chứng minh cho vẻ đẹp của khiêm tốn:
Nhà bác học vĩ đại Enstein: “Tôi chỉ là một người bình thường như bao người khác thôi, cũng sống và làm việc mình yêu thích, sao gọi tôi là người nổi tiếng?”.
Anh Nguyễn Ngọc Mạnh - người đã đỡ cháu bé rơi từ tầng 12 chung cư - đã từ chối danh xưng "người hùng" khi báo chí phỏng vấn. Anh cho rằng mình chỉ là một người bình thường: “Mọi người gọi tôi là anh hùng thì tôi không dám nhận".
- Liên hệ bản thân trong việc rèn luyện lối sống khiêm tốn: bản thân tự nhận thấy đôi lúc mình còn "ngủ quên trong chiến thắng", coi thường người khác,...
3. Kết bài:
- Khẳng định vai trò của lối sống khiêm tốn: Khiêm tốn là đức tính cần có ở mỗi con người.
- Nêu suy nghĩ về hướng rèn luyện của em:
+ Tự ý thức được tầm quan trọng của sống khiêm tốn.
+ Luôn luôn không ngừng học hỏi, tiến lên phía trước, không được tự cao, tự mãn.
1. Mở bài:
- Dẫn dắt vấn đề cần nghị luận. Ví dụ: Những nhân vật vĩ đại thường sống giản dị: Chủ tịch Hồ Chí Minh, Chủ tịch Tôn Đức Thắng,...
- Nêu vấn đề: Cần hình thành lối sống giản dị.
2. Thân bài:
- Nêu quan niệm về lối sống giản dị. Ví dụ: Giản dị là lối sống đơn giản, cần kiệm.
- Nêu biểu hiện của lối sống giản dị trong đời sống:
+ Ăn uống: tiết kiệm, không lãng phí, không bày vẽ.
+ Ăn mặc: đơn giản, không rườm rà, không kiểu cách.
+ Lời nói, cử chỉ: hoà nhã, thân thiện.
+ ...
- Phân tích ý nghĩa của lối sống giản dị:
+ Giúp tiết kiệm tiền bạc, thời gian, công sức.
+ Tạo nên sự hoà đồng, kết nối, cảm thông lớn với mọi người.
+ Một số tấm gương đã chứng minh vẻ đẹp của lối sống giản dị: chủ tịch Hồ Chí Minh, chủ tịch Tôn Đức Thắng,...
- Liên hệ với bản thân trong việc rèn luyện lối sống giản dị: về cơ bản, bản thân đã có ý thức sống tiết kiệm nhưng vẫn có đôi khi vô tình sống lãng phí (quên tắt đèn khi không sử dụng, mua những món đồ ít sử dụng,...)
3. Kết bài:
- Khẳng định vai trò của lối sống giản dị: là phẩm chất cao quý cần có ở mỗi con người.
- Nêu suy nghĩ về hướng rèn luyện của em: học cách sống giản dị từ những biểu hiện nhỏ nhất, tự nhắc bản thân luôn cần kiệm,..
1. Mở bài: Nêu ấn tượng chung về thầy/ cô giáo em yêu quý.
2. Thân bài: Lần lượt trình bày nội dung bài viết theo một trình tự nhất định. Ví dụ:
- Giới thiệu ngắn gọn về thầy/ cô giáo em yêu quý:
+ Tên
+ Tuổi
+ Môn dạy
+ ...
- Phát biểu tình cảm, cảm xúc trước thầy/ cô giáo em yêu quý:
+ Xúc động trước tình yêu nghề và tình yêu học trò của thầy/ cô giáo.
+ Trân trọng sự hi sinh thầm lặng mà thầy/ cô giáo đã dành cho học sinh.
+ Biết ơn những tri thức và bài học cuộc sống mà thầy/ cô giáo đã truyền dạy.
3. Kết bài: Nêu lên suy nghĩ và bài học của cá nhân em về hình ảnh thầy/ cô giáo em yêu quý:
- Tự nhủ sẽ luôn phấn đấu trở thành công dân tốt để không phụ công thầy/ cô giáo đã dạy dỗ.
- Noi theo tấm gương của thầy/ cô giáo, trở thành một người luôn sống có trách nhiệm, tâm huyết với con đường mình chọn.