Bài 2:

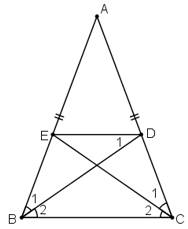
Ta có: ∆ABC là ∆ cân tại A(gt)

=>∠ABC=∠ACB

+Ta có BD là tia pgiac của ∠ABC

=>∠B₁=∠B₂=1/2∠ABC

+Ta có CE là tia pgiac ∠ACB

=>C₁=C₂=1/2∠ACB

Xét ∆

AEC và ΔADB có:

+∠A chung

+AB=AC

+C₁=B₁

=> ΔAEC = ΔADB

=> AE = AD

=>BCDE là hình thang cân

b) Ta có ∠ACB=∠ABC=50^o(do BCDE là hình thang cân)

Ta có: ED//BC

\(\Rightarrow\left\{{}\begin{matrix}\widehat{ABC}=\widehat{AED}\\\widehat{ACB}=\widehat{ADE}\end{matrix}\right.=50^o}\) (SLT)

Mà ∠DEB=∠EDC

Ta có:

+∠DEB+∠AED=180^o (kề bù)

=>50^o+∠AED=180^o

=>∠AED=180^o-50^o=130^o

=>∠AED=∠ADE=130^o

Bài 1:

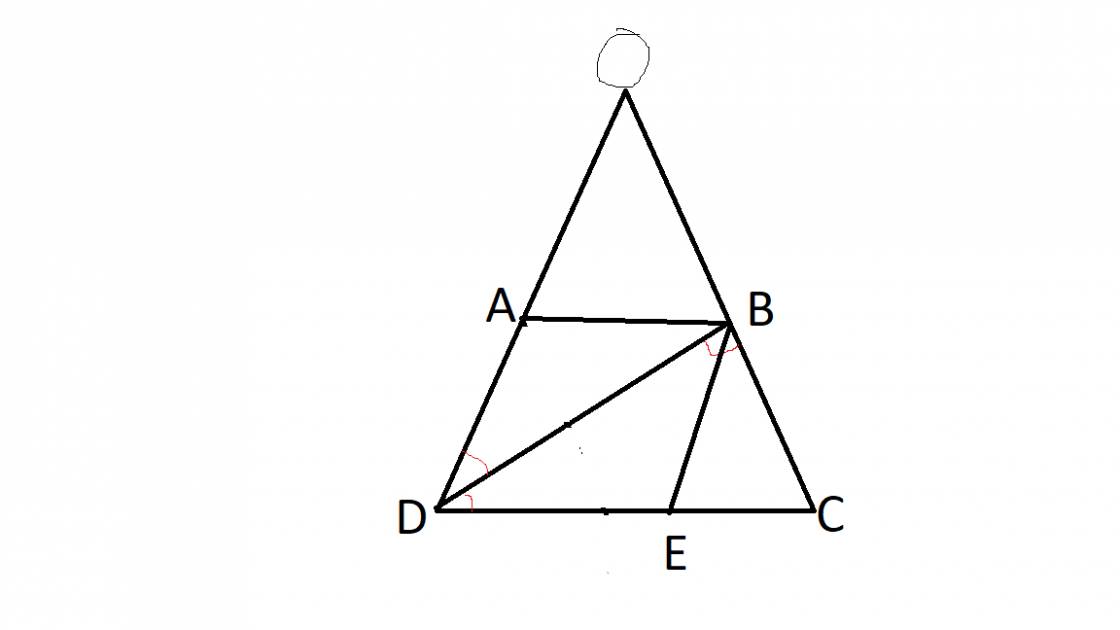
Ta có: AD=BC=3cm (t/c hthang)

Vì AB//CD(gt) nên \(\widehat{ABD}=\widehat{BDC}\left(SLT\right)\)

Mà \(\widehat{ADC}=\widehat{BDC}\) (do BD là tia pgiac góc D)

=>∠ABD=∠BDC 

=>∆ABD cân tại A

=>AD=BC=3cm

Vì ∆DBC vuông tại B

nên ∠BDC+∠C=90^o

Mà ∠ADC=∠C (do ABCD là hình thang cân)

và ∠BDC=1/2 ∠ADC

=> ∠BCD=1/2∠C

Khi đó: ∠C+1/2∠C=90^o=>∠C=60^o

- Kẻ từ B 1 đường thẳng // AD cắt CD tại E

Hình thang ABED có hai cạnh bên song song nên AB = DE và AD = BE

⇒ DE = 3 (cm), BE = 3 (cm)

Mà ∠BEC=∠ADC(đồng vị)

=>∠BEC=∠C

=>∆BEC cân tại B có ∠C=60^o

=>∆BEC là ∆ cả cân cả đều

=> EC=BC=3cm

Ta có: CD = CE + ED = 3 + 3 = 6(cm)

Chu vi hình thang ABCD bằng:

AB + BC + CD + DA = 3 + 3 + 6 + 3 = 15 (cm)

Gọi vốn đơn vị kinh doanh thứ nhất là: x

      vốn đơn vị kinh doanh thứ hai là: y

      vốn đơn vị kinh doanh thứ ba là: z (x,y,z ∈ Z;<650)

Vì ba đơn vị kinh doanh góp vốn theo tỉ lệ 3:4:6, ta có:

                             \(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{x}{6}\)

Vì nếu tổng số tiền lãi là 650 triệu đồng, ta có:

                             \(x+y+z=650\)

Vì tổng số tiền lãi được chia tỉ lệ thuận với số tiền đóng góp, ta có:

                      \(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{6}=\dfrac{x+y+z}{3+4+6}=\dfrac{650000000}{13}=50000000\) 

\(\Rightarrow\left\{{}\begin{matrix}x=50000000.3=150000000\\y=50000000.4=200000000\\z=50000000.6=300000000\end{matrix}\right.\)

Vậy đơn vị thứ nhất được chia 150 triệu

      đơn vị thứ hai được chia: 200 triệu

      đơn vị thứ ba được chia: 300 triệu

Gọi số cần tìm là: \(\overline{abc}\left(a\ne0;\right)a,b,c\inℕ\) 

Ta có \(\overline{abc}=a.100+b.10+c=98a+7b+2a+3c=98\left(a+b+c\right)+\left(a+2b\right)\)

Theo đề bài vì abc chia hết cho 7;98a;7b;a+b+c 

Mà a+2b có kết quả lớn nhất bằng 9+2.9=2 => a+2b có thể = 7, 14, 21

-Nếu a+2b=7 mà 2b là số chẵn =>a<7 và a là số lẻ => a= 1;3;5 <=>b=3;2;1

Ta ghép vào ta có:

+ Với a=1; b=3=> a+b=4 mà tổng a+b+c⁝7

=>c=3=> \(\overline{abc}=133\)

+ Với a=3; b=2 =>a+b=5=>c=2 hoặc 9

=> \(\overline{abc}=322;329\)

Tương tự: Nếu a+2b=14=>a=2;4;6 và b=6;5;4;3

+Với a=2; b=6=>... (như ý trên) => số đó =455

+Với a=6;b=4=>... =>644

+Với a=8;b=3=>...=>833

-Nếu a+2b=21=>a= 3;5;7;9 và b=9;8;7;6

+Với a=3;b=9=>c=2;9=>392 và 399

+Với a=5;b=8=>c=1,8=>581 và 588

+Với a=7;b=7=>c=0,7=>770 và 777

+ Với a=9; b=6=>c=6=> 966

Vậy số tự nhiên đó là: 133;322;329;266;455;644;833;392;399;581;588;770;777;966

số 335 chia hết cho số nguyên tố 5

Đề bài hỏi tìm x hay tính hả bạn?

Số học sinh giỏi là: 

40*1/5=8(học sinh)

Số học sinh còn lại là:

40-8=32(học sinh)

Số học sinh trung bình lớp đó là:

32*3/8=12(học sinh)

Số học sinh khá là:

40-(12+8)=20(học sinh)

đ/s:..

Giả sử ta đặt g(x)=f(x)-f(-x)<=> g(x) là đa thức dạng ax³+bx²+cx+d

Hay mặt khác ta có:

g(1)=f(1)-f(-1)=0

g(-1)=f(-1)-f(1)=0

g(-2)=f(-2)-f(2)=0

g(2)=f(2)-f(-2)=0

=> Từ 4 cái trên g(x) là đa thức bậc không quá 3 mà có 4 nghiệm khác nhau -2;-1;1;2

=> Điều đó không là điều không thể (vô lý)

Vậy phải có a=0; b=0; c=0 và d=0 thì mới có thể xảy ra

<=> f(x)=f(-x) với \(\forall\) x

a) 4.25-12.5+170:10

=100-60+17

=40+17

=57

b) (7+3³:3²).4-3

=(7+3).4-3

=10.4-3

=40-3

=37

c) 12:{400:[500-(125+25.7)]}

=12:{400:[500-(125+175)]}

=12:{400:[500-300]}

=12:{400:200}

=12:2

=6

d) 168+{[2.(2⁴+3²)-256⁰]:7²}

=168+{[2.(16+9)-1]:49}

=168+{[2.25-1]:49}

=168+{[50-1]:49}

=168+{49:49}

=168+1

=169