* Dụng cụ thí nghiệm:

- Máng đứng, có gắn dây rọi (1)

- Vật bằng thép hình trụ (2)

- Nam châm điện N (3), dùng giữ và thả trụ thép

- Cổng quang điện E (4)

- Giá đỡ có đế ba chân, có vít chỉnh cân bằng và trụ thép (5)

- Đồng hồ đo thời gian hiện số (6)

- Công tắc kép (7)

* Các bước tiến hành thí nghiệm:

1. Cắm nam châm điện vào ổ A và cổng quang vào ổ B ở mặt sau của đồng hồ đo thời gian hiện số.

2. Đặt MODE đồng hồ đo thời gian hiện số ở chế độ thích hợp.

3. Đặt trụ thép tại vị trí tiếp cúc với nam châm điện N và bị giữ lại ở đó.

4. Nhấn nút RESET của đồng hồ để chuyến các số hiển thị về giá trị ban đầu 0.000.

5. Nhấn nút của hộp công tắc kép để ngắt điện vào nam châm điện: trụ thép rơi xuống và chuyển động đi qua cổng quang điện.

6. Ghi lại các giá trị thời gian hiển thị trên đồng hồ.

7. Dịch chuyển cổng quang điện ra xa dần nam châm điện, thực hiện lại các thao tác 3, 4, 5, 6 bốn lần nữa. Ghi các giá trị thời gian t tương ứng với quãng đường s.

Chọn trục Ox trùng với chiều dọc của bể bơi, gốc O là điểm xuất phát.

a. Trong lần bơi đầu tiên theo chiều dài của bể bơi

Tốc độ trung bình: \(v_{1} = \frac{s_{1}}{t_{1}} = \frac{50}{40} = 1 , 25\) m/s

Vận tốc trung bình: \(\text{v}_{1} = \frac{d_{1}}{t_{1}} = \frac{50}{40} = 1 , 25\) m/s

b. Trong lần bơi về

Tốc độ trung bình: \(v_{2} = \frac{s_{2}}{t_{2}} = \frac{50}{42} = 1 , 19\) m/s

Vận tốc trung bình: \(\text{v}_{2} = \frac{d_{2}}{t_{2}} = \frac{- 50}{42} = - 1 , 19\) m/s

c. Trong suốt quãng đường đi và về

Tốc độ trung bình: \(v = \frac{s}{t} = \frac{50 + 50}{40 + 42} = 1 , 22\) m/s

Vận tốc trung bình: \(\text{v} = \frac{d}{t} = \frac{0}{40 + 42} = 0\) m/s

v0​=36km/h=10m/s

Quãng đường vật đi được trong 3 giây đầu tiên là: \(s_{3} = \text{v}_{0} t_{3} + \frac{1}{2} a t_{3}^{2} = \text{v}_{0} . 3 + \frac{1}{2} . a . \left(\right. 3^{2} \left.\right) = 3 \text{v}_{0} + \frac{9}{2} a\)

Quãng đường vật đi được trong 4 giây đầu tiên là: \(s_{4} = \text{v}_{0} t_{4} + \frac{1}{2} a t_{4}^{2} = \text{v}_{0} . 4 + \frac{1}{2} . a . \left(\right. 4^{2} \left.\right) = 4 \text{v}_{0} + 8 a\)

Quãng đường vật đi trong giây thứ 4 là: \(\Delta s = s_{4} - s_{3} = \text{v}_{0} + \frac{7}{2} a\)

\(\Rightarrow a = \frac{\Delta s - \text{v}_{0}}{\frac{7}{2}} = \frac{13 , 5 - 10}{\frac{7}{2}} = 1\) m/s²

AB = 4 m; OA = 1 m; OB = 3 m

F₁ = 20 N; F₂ = 100 N; F₃ = 160 N

Theo quy tắc moment lực (thanh AB nằm cân bằng khi tổng các moment lực có xu hướng làm vật quay theo chiều kim đồng hồ bằng với tổng các moment lực có xu hướng làm vật quay ngược chiều kim đồng hồ), ta có:

\(M_{A} + M_{C} = M_{B}\)

\(\Rightarrow F_{1} . O A + F_{3} . O C = F_{2} . O B\)

\(\Rightarrow O C = \frac{F_{2} . O B - F_{1} . O A}{F_{3}} = \frac{100.3 - 20.1}{160} = 1 , 75\) m

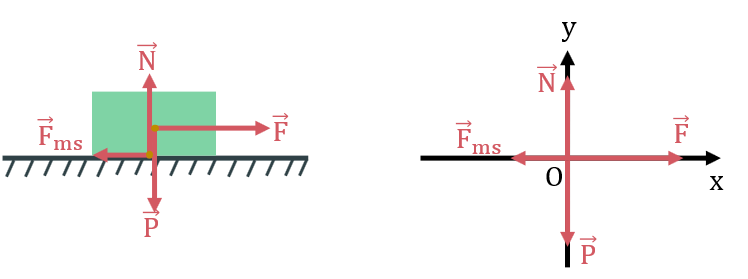
Các lực tác dụng lên vật: trọng lực \(\overset{\rightarrow}{P}\), phản lực \(\overset{\rightarrow}{N}\), lực kéo \(\overset{\rightarrow}{F}\), lực ma sát trượt \(\left(\overset{\rightarrow}{F}\right)_{m s}\)

Áp dụng định luật 2 Newton cho chuyển động của vật theo hai trục Ox, Oy:

\(\left{.F_{x}=F-F_{ms}=ma\\F_{y}=N-P=0}\)

\(\Rightarrow N = P = m g = 12.9 , 8 = 117 , 6\) N

\(F_{m s} = \mu . N = 0 , 2.117 , 6 = 23 , 52\) N

\(\Rightarrow a = \frac{F - F_{m s}}{m} = \frac{30 - 23 , 52}{12} = 0 , 54\) m/s²

Vậy gia tốc có độ lớn 0,54 m/s² và hướng theo chiều chuyển động của thùng.

Ta có: \(\text{v}_{0} = 5.1 0^{5}\) m/s; \(\text{v} = 5 , 4.1 0^{5}\) m/s; \(a = 8.1 0^{4}\) m/s²

Thời gian electron bay được trong khi được gia tốc là:

\(t = \frac{\text{v} - \text{v}_{0}}{a} = \frac{5 , 4.1 0^{5} - 5.1 0^{5}}{8.1 0^{4}} = 0 , 5 s\)

Quãng đường electron bay được trong khi được gia tốc là:

\(s = \frac{\text{v}^{2} - \text{v}_{0}^{2}}{2 a} = \frac{\left(\left(\right. 5 , 4.1 0^{5} \left.\right)\right)^{2} - \left(\left(\right. 5.1 0^{5} \left.\right)\right)^{2}}{2.8.1 0^{4}} = 26.1 0^{4} m\)

a. Độ cao của nơi thả viên bi so với mặt đất là:

\(h = \frac{1}{2} g t^{2} = \frac{1}{2} . 9 , 8. 3^{2} = 44 , 1\) m

b. Vận tốc lúc chạm đất là:

\(\text{v} = g t = 9 , 8.3 = 29 , 4\) m/s

c. Quãng đường vật rơi trong 2,5 s đầu là:

\(s_{1} = \frac{1}{2} g t_{1}^{2} = \frac{1}{2} . 9 , 8.2 , 5^{2} = 30 , 625\) m

Quãng đường vật rơi trong 0,5 s cuối là:

\(s = h - s_{1} = 44 , 1 - 30 , 625 = 13 , 475\) m

Gọi \(s\) là quãng đường viên đá đi được sau khoảng thời gian \(t\) kể từ khi bắt đầu rơi tới khi chạm đất

\(s_{1}\) là quãng đường viên đá đi được trước khi chạm đất 1 s, tức là sau khoảng thời gian \(t_{1} = t - 1\)

Ta có: \(s = \frac{1}{2} g t^{2}\) và \(s_{1} = \frac{1}{2} g \left(\left(\right. t - 1 \left.\right)\right)^{2}\)

Quãng đường viên đá đi được trong 1 s cuối trước khi chạm đất là:

\(\Delta s = s - s_{1} = \frac{1}{2} g t^{2} - \frac{1}{2} g \left(\left(\right. t - 1 \left.\right)\right)^{2} = g t - \frac{1}{2} g\)

\(\Rightarrow t = \frac{\Delta s}{g} + \frac{1}{2} = \frac{14 , 7}{9 , 8} + \frac{1}{2} = 2\) s

a. Vẽ đồ thị độ dịch chuyển – thời gian của Nam.

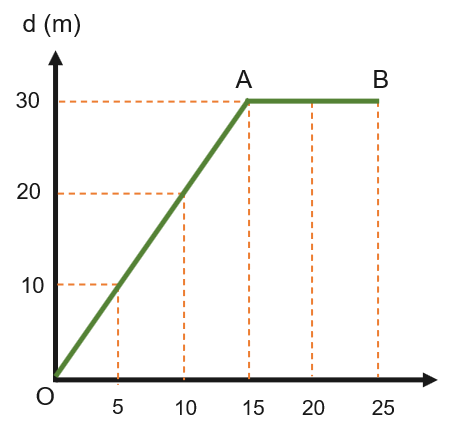
b. Mô tả chuyển động của Nam:

- Từ 0 – 15 giây: Nam chuyển động thẳng đều với vận tốc: \(\text{v}_{1} = \frac{\Delta d_{1}}{\Delta t_{1}} = \frac{30}{15} = 2\) m/s

- Từ giây thứ 15 đến giây thứ 25: Nam đứng yên (dừng lại).

c. Vận tốc của Nam trong 15 s đầu là:

\(\text{v}_{1} = \frac{\Delta d_{1}}{\Delta t_{1}} = \frac{30}{15} = 2\) m/s

Vận tốc của Nam trong suốt quá trình chuyển động:

\(\text{v} = \frac{\Delta d}{\Delta t} = \frac{30}{25} = 1 , 2\) m/s

Chọn chiều dương là chiều chuyển động của ô tô, gốc thời gian lúc bắt đầu hãm phanh.

Đổi 64,8 km/h = 18 m/s; 54 km/h = 15 m/s; 36 km/h = 10 m/s

a. Gia tốc của ô tô:

\(a = \frac{\text{v}_{1} - \text{v}_{0}}{\Delta t} = \frac{15 - 18}{10} = - 0 , 3\) m/s²

Thời gian kể từ khi hãm phanh đến khi ô tô đạt vận tốc v₂ = 36 km/h = 10 m/s là:

\(\text{v} = \text{v}_{0} + a t \Rightarrow t = \frac{\text{v}_{2} - \text{v}_{0}}{a} = \frac{10 - 18}{- 0 , 3} = 26 , 7\) s

b. Thời gian kể từ khi hãm phanh đến khi ô tô dừng hẳn \(\text{v}_{3} = 0\) là:

\(t^{'} = \frac{\text{v}_{3} - \text{v}_{0}}{a} = \frac{0 - 18}{- 0 , 3} = 60\) s

c. Ta có: \(\text{v}_{2}^{2} - \text{v}_{0}^{2} = 2 a s\)

Vậy quãng đường ô tô đi được đến khi dừng hẳn là:

\(s = \frac{\text{v}_{3}^{2} - \text{v}_{0}^{2}}{2 a} = \frac{0 - 1 8^{2}}{2 \left(\right. - 0 , 3 \left.\right)} = 540\) m