Giả sử: Bình là người giấu chìa khóa

Xét lời nói từng người:

• An:
• • "Không phải Đạt giấu" → Đúng
  • "Là Bình giấu" → Đúng
    ⇒ Cả hai đúng → Loại

Giả sử: Chi là người giấu

• An:
• • "Không phải Đạt giấu" → Không phải Đạt → đúng
  • "Là Bình giấu" → Sai
    → Hợp lệ (1 đúng, 1 sai)
• Bình:
• • "Không phải Chi giấu" → Sai
  • "Cũng không phải Đạt giấu" → đúng
    → Hợp lệ
• Chi:
• • "Đạt giấu" → Sai
  • "Không phải An giấu" → Đúng
    → Hợp lệ
• Dũng:
• • "Chi giấu" → Đúng
  • "Bình giấu" → Sai
    → Hợp lệ
• Đạt:
• • "Dũng giấu" → Sai
  • "Không phải An giấu" → Đúng
    → Hợp lệ

Tất cả đều nói 1 thật, 1 sai → Thoả mãn

Kết luận: Chi là người đang giấu chìa khóa.

những người Anh sang sống ở việt thì học tiếng việt

giữ tinh thần thật thoải mái và sẵn sàng.

1. Phương trình a)

\(x^{4} + x^{3} + 4 x^{2} + 5 x + 25 = 0.\)

Bước 1: Giả sử phân tích

Giả sử

\(x^{4} + x^{3} + 4 x^{2} + 5 x + 25 = \left(\right. x^{2} + p x + q \left.\right) \left(\right. x^{2} + r x + s \left.\right) .\)

Khi đó, bằng cách nhân và so sánh hệ số với đa thức gốc:

• Hệ số \(x^{3}\): \(p + r = 1.\)
• Hệ số \(x^{2}\): \(p r + q + s = 4.\)
• Hệ số \(x^{1}\): \(p s + q r = 5.\)
• Hằng số: \(q s = 25.\)

Bước 2: Tìm \(p , q , r , s\)

Từ \(q s = 25\). Các khả năng (với hệ số thực) là cặp \(\left(\right. q , s \left.\right)\) sao cho tích 25. Thông thường ta thử nghiệm cặp kiểu số nguyên hoặc đơn giản:

• Ta thử \(q = 5 , \textrm{ } s = 5\). Khi đó:
  Giờ giải hệ
  \(\left{\right. p + r = 1 , \\ p r = - 6.\)
  Giải: \(p , r\) là nghiệm của phương trình \(t^{2} - \left(\right. p + r \left.\right) t + p r = 0 \Longrightarrow t^{2} - 1 \cdot t - 6 = 0 \Longrightarrow t^{2} - t - 6 = 0.\)
  Giải: \(t = \frac{1 \pm \sqrt{1 + 24}}{2} = \frac{1 \pm 5}{2} .\)
  ⇒ \(t = 3\) hoặc \(t = - 2.\)
  Vì \(p + r = 1\), nên một trong hai là 3, một là -2. Ví dụ:
• • \(p r + 5 + 5 = 4 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } p r = 4 - 10 = - 6.\)
  • \(p + r = 1.\)
  • Và \(p s + q r = 5 p + 5 r = 5 \left(\right. p + r \left.\right) = 5 \cdot 1 = 5.\) (thỏa điều kiện hệ số \(x^{1}\) = 5) ⇒ phù hợp.
• • \(p = 3 , r = - 2 ,\) hoặc ngược lại \(p = - 2 , r = 3.\) Cả hai cho ra tích \(p r = - 6\) và tổng 1.

Ta có thể lấy \(p = 3 , r = - 2\). Khi đó

\(x^{4} + x^{3} + 4 x^{2} + 5 x + 25 = \left(\right. x^{2} + 3 x + 5 \left.\right) \left(\right. x^{2} - 2 x + 5 \left.\right) .\)

Bước 3: Giải phương trình

\(\left(\right. x^{2} + 3 x + 5 \left.\right) \left(\right. x^{2} - 2 x + 5 \left.\right) = 0\)

Cho hai phương trình bậc hai:

1. \(x^{2} + 3 x + 5 = 0\).
   Discriminant \(\Delta = 3^{2} - 4 \cdot 1 \cdot 5 = 9 - 20 = - 11 < 0.\)
   ⇒ Nghiệm phức:
   \(x = \frac{- 3 \pm \sqrt{- 11}}{2} = - \frac{3}{2} \pm \frac{\sqrt{11}}{2} \textrm{ } i .\)
2. \(x^{2} - 2 x + 5 = 0\).
   Discriminant \(\Delta = \left(\right. - 2 \left.\right)^{2} - 4 \cdot 1 \cdot 5 = 4 - 20 = - 16 < 0.\)
   ⇒ Nghiệm phức:
   \(x = \frac{2 \pm \sqrt{- 16}}{2} = 1 \pm 2 i .\)

Kết luận a)

Phương trình không có nghiệm thực, có 4 nghiệm phức:

\(x = - \frac{3}{2} \pm \frac{\sqrt{11}}{2} i , x = 1 \pm 2 i .\)

2. Phương trình b)

\(x^{4} + 3 x^{3} - 14 x^{2} - 6 x + 4 = 0.\)

Bước 1: Giả sử phân tích

\(x^{4} + 3 x^{3} - 14 x^{2} - 6 x + 4 = \left(\right. x^{2} + p x + q \left.\right) \left(\right. x^{2} + r x + s \left.\right) .\)

So sánh:

• \(p + r = 3.\)
• \(p r + q + s = - 14.\)
• \(p s + q r = - 6.\)
• \(q s = 4.\)

Bước 2: Tìm \(q , s\) sao cho \(q s = 4\).

Thử các cặp đơn giản: \(\left(\right. 1 , 4 \left.\right) , \left(\right. 2 , 2 \left.\right) , \left(\right. 4 , 1 \left.\right) , \left(\right. - 1 , - 4 \left.\right) , \left(\right. - 2 , - 2 \left.\right) , \left(\right. - 4 , - 1 \left.\right)\). Kiểm tra xem có thỏa hệ hay không.

• Thử \(q = - 2 , s = - 2\) (tích 4).
  Khi đó:
• • \(p r + \left(\right. - 2 \left.\right) + \left(\right. - 2 \left.\right) = - 14 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } p r - 4 = - 14 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } p r = - 10.\)
  • \(p + r = 3.\)
  • Kiểm tra điều kiện \(p s + q r = p \left(\right. - 2 \left.\right) + \left(\right. - 2 \left.\right) r = - 2 p - 2 r = - 2 \left(\right. p + r \left.\right) = - 2 \cdot 3 = - 6.\) Đúng khớp với hệ số \(- 6\).
    Thỏa!
    Giải hệ \(p + r = 3 , p r = - 10.\)
    ⇒ \(t^{2} - 3 t - 10 = 0 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } t = \frac{3 \pm \sqrt{9 + 40}}{2} = \frac{3 \pm 7}{2} .\)
    ⇒ \(t = 5\) hoặc \(t = - 2.\) Vì tổng 3 nên một là 5, một là -2. Ví dụ \(p = 5 , r = - 2\) hoặc ngược lại.

Chọn \(p = 5 , r = - 2\). Khi đó

\(x^{4} + 3 x^{3} - 14 x^{2} - 6 x + 4 = \left(\right. x^{2} + 5 x - 2 \left.\right) \left(\right. x^{2} - 2 x - 2 \left.\right) .\)

Bước 3: Giải hai phương trình bậc hai

1. \(x^{2} + 5 x - 2 = 0\).
   Discriminant \(\Delta = 5^{2} - 4 \cdot 1 \cdot \left(\right. - 2 \left.\right) = 25 + 8 = 33.\)
   \(x = \frac{- 5 \pm \sqrt{33}}{2} .\)
2. \(x^{2} - 2 x - 2 = 0\).
   Discriminant \(\Delta = \left(\right. - 2 \left.\right)^{2} - 4 \cdot 1 \cdot \left(\right. - 2 \left.\right) = 4 + 8 = 12.\)
   \(x = \frac{2 \pm \sqrt{12}}{2} = \frac{2 \pm 2 \sqrt{3}}{2} = 1 \pm \sqrt{3} .\)

Kết luận b)

Phương trình có 4 nghiệm thực:

\(x = \frac{- 5 + \sqrt{33}}{2} , x = \frac{- 5 - \sqrt{33}}{2} , x = 1 + \sqrt{3} , x = 1 - \sqrt{3} .\)

3. Phương trình c)

\(x^{4} + 5 x^{3} - 14 x^{2} - 20 x + 16 = 0.\)

Bước 1: Giả sử phân tích

\(x^{4} + 5 x^{3} - 14 x^{2} - 20 x + 16 = \left(\right. x^{2} + p x + q \left.\right) \left(\right. x^{2} + r x + s \left.\right) .\)

So sánh:

• \(p + r = 5.\)
• \(p r + q + s = - 14.\)
• \(p s + q r = - 20.\)
• \(q s = 16.\)

Bước 2: Tìm \(q , s\) sao cho \(q s = 16\).

Thử cặp đơn giản: có thể \(q = - 4 , s = - 4\) cho tích 16. Kiểm tra:

• Nếu \(q = - 4 , s = - 4\):
• • \(p r + \left(\right. - 4 \left.\right) + \left(\right. - 4 \left.\right) = - 14 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } p r - 8 = - 14 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } p r = - 6.\)
  • \(p + r = 5.\)
  • Kiểm tra \(p s + q r = p \left(\right. - 4 \left.\right) + \left(\right. - 4 \left.\right) r = - 4 p - 4 r = - 4 \left(\right. p + r \left.\right) = - 4 \cdot 5 = - 20.\) Đúng khớp.
    ⇒ Hệ \(p + r = 5 , p r = - 6\).
    ⇒ \(t^{2} - 5 t - 6 = 0 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } t = \frac{5 \pm \sqrt{25 + 24}}{2} = \frac{5 \pm 7}{2} .\)
    ⇒ \(t = 6\) hoặc \(t = - 1\). Tổng 5 ⇒ một là 6, một là -1. Ví dụ \(p = 6 , r = - 1\) hoặc ngược lại.

Chọn \(p = 6 , r = - 1\). Khi đó

\(x^{4} + 5 x^{3} - 14 x^{2} - 20 x + 16 = \left(\right. x^{2} + 6 x - 4 \left.\right) \left(\right. x^{2} - x - 4 \left.\right) .\)

Bước 3: Giải hai phương trình bậc hai

1. \(x^{2} + 6 x - 4 = 0\).
   Discriminant \(\Delta = 36 - 4 \cdot 1 \cdot \left(\right. - 4 \left.\right) = 36 + 16 = 52 = 4 \cdot 13.\)
   \(x = \frac{- 6 \pm \sqrt{52}}{2} = \frac{- 6 \pm 2 \sqrt{13}}{2} = - 3 \pm \sqrt{13} .\)
2. \(x^{2} - x - 4 = 0\).
   Discriminant \(\Delta = 1 - 4 \cdot 1 \cdot \left(\right. - 4 \left.\right) = 1 + 16 = 17.\)
   \(x = \frac{1 \pm \sqrt{17}}{2} .\)

Kết luận c)

Phương trình có 4 nghiệm thực:

\(x = - 3 + \sqrt{13} , x = - 3 - \sqrt{13} , x = \frac{1 + \sqrt{17}}{2} , x = \frac{1 - \sqrt{17}}{2} .\)

4. Phương trình d)

\(3 x^{4} + 2 x^{3} - 13 x^{2} - 4 x + 12 = 0.\)

Bước 1: Thử tách nhân tử

Ở đây hệ số cao nhất là 3. Thông thường ta cũng kiểm tra xem có nghiệm hữu tỉ dạng \(\pm 1 , \pm 2 , \pm 3 , \pm 4 , \pm 6 , \pm 12 , \ldots\) theo định lý nghiệm hữu tỉ (ước của 12 trên ước của 3). Thử lần lượt:

• Thử \(x = 1\): \(3 + 2 - 13 - 4 + 12 = 0.\) ⇒ \(1\) là nghiệm thực.
• Thử \(x = - 2\): \(3 \cdot 16 + 2 \cdot \left(\right. - 8 \left.\right) - 13 \cdot 4 - 4 \cdot \left(\right. - 2 \left.\right) + 12 = 48 - 16 - 52 + 8 + 12 = 0.\) ⇒ \(x = - 2\) cũng là nghiệm thực.

Vậy đa thức có nhân tử \(\left(\right. x - 1 \left.\right) \left(\right. x + 2 \left.\right)\). Chia đa thức cho \(\left(\right. x - 1 \left.\right) \left(\right. x + 2 \left.\right)\) hoặc lặp lại phép chia đa thức:

Bước 2: Chia đa thức

Chia \(3 x^{4} + 2 x^{3} - 13 x^{2} - 4 x + 12\) cho \(\left(\right. x - 1 \left.\right)\) trước:

• Dùng phép chia đa thức hoặc tổng quát biết rằng sau khi tách \(x = 1\) và \(x = - 2\), ta có thể viết
  \(3 x^{4} + 2 x^{3} - 13 x^{2} - 4 x + 12 = \left(\right. x - 1 \left.\right) \left(\right. x + 2 \left.\right) \left(\right. đ\text{a}\&\text{nbsp};\text{th}ứ\text{c}\&\text{nbsp};\text{b}ậ\text{c}\&\text{nbsp};\text{2} \left.\right) .\)

Thực hiện nhanh phép chia (hoặc dùng Euclid) sẽ cho đa thức bậc 2 là \(3 x^{2} - x - 6\). Bạn có thể kiểm tra:

\(\left(\right. x - 1 \left.\right) \left(\right. x + 2 \left.\right) \left(\right. 3 x^{2} - x - 6 \left.\right) = \left(\right. x^{2} + x - 2 \left.\right) \left(\right. 3 x^{2} - x - 6 \left.\right) .\)

Nhân ra sẽ thu lại đa thức gốc (có thể tự kiểm tra).

Bước 3: Giải đa thức bậc hai còn lại

Giải \(3 x^{2} - x - 6 = 0\).
Discriminant \(\Delta = \left(\right. - 1 \left.\right)^{2} - 4 \cdot 3 \cdot \left(\right. - 6 \left.\right) = 1 + 72 = 73.\)

\(x = \frac{1 \pm \sqrt{73}}{2 \cdot 3} = \frac{1 \pm \sqrt{73}}{6} .\)

Kết luận d)

Phương trình có 4 nghiệm thực:

\(x = 1 , x = - 2 , x = \frac{1 + \sqrt{73}}{6} , x = \frac{1 - \sqrt{73}}{6} .\)

1. Phương trình a)

\(x^{4} + x^{3} + 4 x^{2} + 5 x + 25 = 0.\)

Bước 1: Giả sử phân tích

Giả sử

\(x^{4} + x^{3} + 4 x^{2} + 5 x + 25 = \left(\right. x^{2} + p x + q \left.\right) \left(\right. x^{2} + r x + s \left.\right) .\)

Khi đó, bằng cách nhân và so sánh hệ số với đa thức gốc:

• Hệ số \(x^{3}\): \(p + r = 1.\)
• Hệ số \(x^{2}\): \(p r + q + s = 4.\)
• Hệ số \(x^{1}\): \(p s + q r = 5.\)
• Hằng số: \(q s = 25.\)

Bước 2: Tìm \(p , q , r , s\)

Từ \(q s = 25\). Các khả năng (với hệ số thực) là cặp \(\left(\right. q , s \left.\right)\) sao cho tích 25. Thông thường ta thử nghiệm cặp kiểu số nguyên hoặc đơn giản:

• Ta thử \(q = 5 , \textrm{ } s = 5\). Khi đó:
  Giờ giải hệ
  \(\left{\right. p + r = 1 , \\ p r = - 6.\)
  Giải: \(p , r\) là nghiệm của phương trình \(t^{2} - \left(\right. p + r \left.\right) t + p r = 0 \Longrightarrow t^{2} - 1 \cdot t - 6 = 0 \Longrightarrow t^{2} - t - 6 = 0.\)
  Giải: \(t = \frac{1 \pm \sqrt{1 + 24}}{2} = \frac{1 \pm 5}{2} .\)
  ⇒ \(t = 3\) hoặc \(t = - 2.\)
  Vì \(p + r = 1\), nên một trong hai là 3, một là -2. Ví dụ:
• • \(p r + 5 + 5 = 4 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } p r = 4 - 10 = - 6.\)
  • \(p + r = 1.\)
  • Và \(p s + q r = 5 p + 5 r = 5 \left(\right. p + r \left.\right) = 5 \cdot 1 = 5.\) (thỏa điều kiện hệ số \(x^{1}\) = 5) ⇒ phù hợp.
• • \(p = 3 , r = - 2 ,\) hoặc ngược lại \(p = - 2 , r = 3.\) Cả hai cho ra tích \(p r = - 6\) và tổng 1.

Ta có thể lấy \(p = 3 , r = - 2\). Khi đó

\(x^{4} + x^{3} + 4 x^{2} + 5 x + 25 = \left(\right. x^{2} + 3 x + 5 \left.\right) \left(\right. x^{2} - 2 x + 5 \left.\right) .\)

Bước 3: Giải phương trình

\(\left(\right. x^{2} + 3 x + 5 \left.\right) \left(\right. x^{2} - 2 x + 5 \left.\right) = 0\)

Cho hai phương trình bậc hai:

1. \(x^{2} + 3 x + 5 = 0\).
   Discriminant \(\Delta = 3^{2} - 4 \cdot 1 \cdot 5 = 9 - 20 = - 11 < 0.\)
   ⇒ Nghiệm phức:
   \(x = \frac{- 3 \pm \sqrt{- 11}}{2} = - \frac{3}{2} \pm \frac{\sqrt{11}}{2} \textrm{ } i .\)
2. \(x^{2} - 2 x + 5 = 0\).
   Discriminant \(\Delta = \left(\right. - 2 \left.\right)^{2} - 4 \cdot 1 \cdot 5 = 4 - 20 = - 16 < 0.\)
   ⇒ Nghiệm phức:
   \(x = \frac{2 \pm \sqrt{- 16}}{2} = 1 \pm 2 i .\)

Kết luận a)

Phương trình không có nghiệm thực, có 4 nghiệm phức:

\(x = - \frac{3}{2} \pm \frac{\sqrt{11}}{2} i , x = 1 \pm 2 i .\)

2. Phương trình b)

\(x^{4} + 3 x^{3} - 14 x^{2} - 6 x + 4 = 0.\)

Bước 1: Giả sử phân tích

\(x^{4} + 3 x^{3} - 14 x^{2} - 6 x + 4 = \left(\right. x^{2} + p x + q \left.\right) \left(\right. x^{2} + r x + s \left.\right) .\)

So sánh:

• \(p + r = 3.\)
• \(p r + q + s = - 14.\)
• \(p s + q r = - 6.\)
• \(q s = 4.\)

Bước 2: Tìm \(q , s\) sao cho \(q s = 4\).

Thử các cặp đơn giản: \(\left(\right. 1 , 4 \left.\right) , \left(\right. 2 , 2 \left.\right) , \left(\right. 4 , 1 \left.\right) , \left(\right. - 1 , - 4 \left.\right) , \left(\right. - 2 , - 2 \left.\right) , \left(\right. - 4 , - 1 \left.\right)\). Kiểm tra xem có thỏa hệ hay không.

• Thử \(q = - 2 , s = - 2\) (tích 4).
  Khi đó:
• • \(p r + \left(\right. - 2 \left.\right) + \left(\right. - 2 \left.\right) = - 14 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } p r - 4 = - 14 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } p r = - 10.\)
  • \(p + r = 3.\)
  • Kiểm tra điều kiện \(p s + q r = p \left(\right. - 2 \left.\right) + \left(\right. - 2 \left.\right) r = - 2 p - 2 r = - 2 \left(\right. p + r \left.\right) = - 2 \cdot 3 = - 6.\) Đúng khớp với hệ số \(- 6\).
    Thỏa!
    Giải hệ \(p + r = 3 , p r = - 10.\)
    ⇒ \(t^{2} - 3 t - 10 = 0 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } t = \frac{3 \pm \sqrt{9 + 40}}{2} = \frac{3 \pm 7}{2} .\)
    ⇒ \(t = 5\) hoặc \(t = - 2.\) Vì tổng 3 nên một là 5, một là -2. Ví dụ \(p = 5 , r = - 2\) hoặc ngược lại.

Chọn \(p = 5 , r = - 2\). Khi đó

\(x^{4} + 3 x^{3} - 14 x^{2} - 6 x + 4 = \left(\right. x^{2} + 5 x - 2 \left.\right) \left(\right. x^{2} - 2 x - 2 \left.\right) .\)

Bước 3: Giải hai phương trình bậc hai

1. \(x^{2} + 5 x - 2 = 0\).
   Discriminant \(\Delta = 5^{2} - 4 \cdot 1 \cdot \left(\right. - 2 \left.\right) = 25 + 8 = 33.\)
   \(x = \frac{- 5 \pm \sqrt{33}}{2} .\)
2. \(x^{2} - 2 x - 2 = 0\).
   Discriminant \(\Delta = \left(\right. - 2 \left.\right)^{2} - 4 \cdot 1 \cdot \left(\right. - 2 \left.\right) = 4 + 8 = 12.\)
   \(x = \frac{2 \pm \sqrt{12}}{2} = \frac{2 \pm 2 \sqrt{3}}{2} = 1 \pm \sqrt{3} .\)

Kết luận b)

Phương trình có 4 nghiệm thực:

\(x = \frac{- 5 + \sqrt{33}}{2} , x = \frac{- 5 - \sqrt{33}}{2} , x = 1 + \sqrt{3} , x = 1 - \sqrt{3} .\)

3. Phương trình c)

\(x^{4} + 5 x^{3} - 14 x^{2} - 20 x + 16 = 0.\)

Bước 1: Giả sử phân tích

\(x^{4} + 5 x^{3} - 14 x^{2} - 20 x + 16 = \left(\right. x^{2} + p x + q \left.\right) \left(\right. x^{2} + r x + s \left.\right) .\)

So sánh:

• \(p + r = 5.\)
• \(p r + q + s = - 14.\)
• \(p s + q r = - 20.\)
• \(q s = 16.\)

Bước 2: Tìm \(q , s\) sao cho \(q s = 16\).

Thử cặp đơn giản: có thể \(q = - 4 , s = - 4\) cho tích 16. Kiểm tra:

• Nếu \(q = - 4 , s = - 4\):
• • \(p r + \left(\right. - 4 \left.\right) + \left(\right. - 4 \left.\right) = - 14 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } p r - 8 = - 14 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } p r = - 6.\)
  • \(p + r = 5.\)
  • Kiểm tra \(p s + q r = p \left(\right. - 4 \left.\right) + \left(\right. - 4 \left.\right) r = - 4 p - 4 r = - 4 \left(\right. p + r \left.\right) = - 4 \cdot 5 = - 20.\) Đúng khớp.
    ⇒ Hệ \(p + r = 5 , p r = - 6\).
    ⇒ \(t^{2} - 5 t - 6 = 0 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } t = \frac{5 \pm \sqrt{25 + 24}}{2} = \frac{5 \pm 7}{2} .\)
    ⇒ \(t = 6\) hoặc \(t = - 1\). Tổng 5 ⇒ một là 6, một là -1. Ví dụ \(p = 6 , r = - 1\) hoặc ngược lại.

Chọn \(p = 6 , r = - 1\). Khi đó

\(x^{4} + 5 x^{3} - 14 x^{2} - 20 x + 16 = \left(\right. x^{2} + 6 x - 4 \left.\right) \left(\right. x^{2} - x - 4 \left.\right) .\)

Bước 3: Giải hai phương trình bậc hai

1. \(x^{2} + 6 x - 4 = 0\).
   Discriminant \(\Delta = 36 - 4 \cdot 1 \cdot \left(\right. - 4 \left.\right) = 36 + 16 = 52 = 4 \cdot 13.\)
   \(x = \frac{- 6 \pm \sqrt{52}}{2} = \frac{- 6 \pm 2 \sqrt{13}}{2} = - 3 \pm \sqrt{13} .\)
2. \(x^{2} - x - 4 = 0\).
   Discriminant \(\Delta = 1 - 4 \cdot 1 \cdot \left(\right. - 4 \left.\right) = 1 + 16 = 17.\)
   \(x = \frac{1 \pm \sqrt{17}}{2} .\)

Kết luận c)

Phương trình có 4 nghiệm thực:

\(x = - 3 + \sqrt{13} , x = - 3 - \sqrt{13} , x = \frac{1 + \sqrt{17}}{2} , x = \frac{1 - \sqrt{17}}{2} .\)

4. Phương trình d)

\(3 x^{4} + 2 x^{3} - 13 x^{2} - 4 x + 12 = 0.\)

Bước 1: Thử tách nhân tử

Ở đây hệ số cao nhất là 3. Thông thường ta cũng kiểm tra xem có nghiệm hữu tỉ dạng \(\pm 1 , \pm 2 , \pm 3 , \pm 4 , \pm 6 , \pm 12 , \ldots\) theo định lý nghiệm hữu tỉ (ước của 12 trên ước của 3). Thử lần lượt:

• Thử \(x = 1\): \(3 + 2 - 13 - 4 + 12 = 0.\) ⇒ \(1\) là nghiệm thực.
• Thử \(x = - 2\): \(3 \cdot 16 + 2 \cdot \left(\right. - 8 \left.\right) - 13 \cdot 4 - 4 \cdot \left(\right. - 2 \left.\right) + 12 = 48 - 16 - 52 + 8 + 12 = 0.\) ⇒ \(x = - 2\) cũng là nghiệm thực.

Vậy đa thức có nhân tử \(\left(\right. x - 1 \left.\right) \left(\right. x + 2 \left.\right)\). Chia đa thức cho \(\left(\right. x - 1 \left.\right) \left(\right. x + 2 \left.\right)\) hoặc lặp lại phép chia đa thức:

Bước 2: Chia đa thức

Chia \(3 x^{4} + 2 x^{3} - 13 x^{2} - 4 x + 12\) cho \(\left(\right. x - 1 \left.\right)\) trước:

• Dùng phép chia đa thức hoặc tổng quát biết rằng sau khi tách \(x = 1\) và \(x = - 2\), ta có thể viết
  \(3 x^{4} + 2 x^{3} - 13 x^{2} - 4 x + 12 = \left(\right. x - 1 \left.\right) \left(\right. x + 2 \left.\right) \left(\right. đ\text{a}\&\text{nbsp};\text{th}ứ\text{c}\&\text{nbsp};\text{b}ậ\text{c}\&\text{nbsp};\text{2} \left.\right) .\)

Thực hiện nhanh phép chia (hoặc dùng Euclid) sẽ cho đa thức bậc 2 là \(3 x^{2} - x - 6\). Bạn có thể kiểm tra:

\(\left(\right. x - 1 \left.\right) \left(\right. x + 2 \left.\right) \left(\right. 3 x^{2} - x - 6 \left.\right) = \left(\right. x^{2} + x - 2 \left.\right) \left(\right. 3 x^{2} - x - 6 \left.\right) .\)

Nhân ra sẽ thu lại đa thức gốc (có thể tự kiểm tra).

Bước 3: Giải đa thức bậc hai còn lại

Giải \(3 x^{2} - x - 6 = 0\).
Discriminant \(\Delta = \left(\right. - 1 \left.\right)^{2} - 4 \cdot 3 \cdot \left(\right. - 6 \left.\right) = 1 + 72 = 73.\)

\(x = \frac{1 \pm \sqrt{73}}{2 \cdot 3} = \frac{1 \pm \sqrt{73}}{6} .\)

Kết luận d)

Phương trình có 4 nghiệm thực:

\(x = 1 , x = - 2 , x = \frac{1 + \sqrt{73}}{6} , x = \frac{1 - \sqrt{73}}{6} .\)

a) Ta có \(a \bot c\) và \(b \bot c\) nên \(a\) // \(b\) (tính chất từ vuông góc đến song song).

b) 

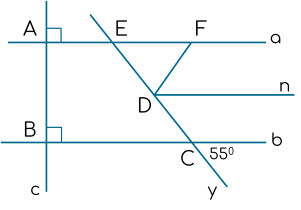
Ta có \(\hat{b C y} = \hat{E C B} = 5 5^{\circ}\).

Vì \(a\) // \(b\) nên \(\hat{E C B} = \hat{F E D} = 5 5^{\circ}\).

Vì \(D n\) là tia phân giác của \(\hat{F D C}\) nên \(\hat{C D n} = \frac{1}{2} . \hat{F D C} = 5 5^{\circ}\).

Nên \(\hat{F E D} = \hat{C D n}\) mà hai góc này ở vị trí đồng vị nên \(D n\) // \(a\).

Ta có \(\hat{x B A} = \hat{B A D} = 5 0^{\circ}\).

Hai góc này ở vị trí so le trong nên \(B x\) // \(A D\) (1).

Ta có \(\hat{D A C} = \hat{A C y} = 3 0^{\circ}\).

Hai góc này ở vị trí so le trong nên \(C y\) // \(A D\) (2).

Từ (1) và (2) suy ra \(B x\) // \(C y\) (cùng song song với \(A D\)).

"Tam giác" là một hình có ba cạnh, hay còn gọi là "ba cạnh" → đọc lái đi sẽ thành "ba cạnh" = Ba Cạnh = Bà Cạnh.
Bà Cạnh nghe gần giống như bà của Trang → nên người ta gọi cô gái đó là Trang.

Hoặc hiểu đơn giản hơn:
Tam giác → 3 cạnh → "ba cạnh" → bà Cạnh → cháu của bà Cạnh là Trang.
Vậy cô gái tên là Trang.

Chiến dịch Manhattan (Manhattan Project) – đây là tên gọi của chương trình nghiên cứu và phát triển vũ khí hạt nhân, dẫn đến việc chế tạo thành công bom nguyên tử.

Còn chiến dịch ném bom thực tế xuống Nhật Bản có hai vụ chính:

1. Ngày 6 tháng 8 năm 1945: Mỹ ném bom nguyên tử "Little Boy" xuống thành phố Hiroshima.
2. Ngày 9 tháng 8 năm 1945: Mỹ ném bom nguyên tử "Fat Man" xuống thành phố Nagasaki.

• Bơ động vật:

• Đã cho: 220g

• Đường bột:

• Mỗi túi: 62,5g
• 2 túi: \(62 , 5 \times 2 = 125 g\)

• Trứng gà (đã bỏ vỏ):

• 3 quả, mỗi quả: 55,5g
• Tổng: \(55 , 5 \times 3 = 166 , 5 g\)

• Bột mì:

• Đã cho: 350,5g

2. Tính tổng khối lượng tất cả nguyên liệu:

\(220 + 125 + 166 , 5 + 350 , 5 = 862 g\)

3. Tính lượng nguyên liệu cho mỗi chiếc bánh

• Có 50 chiếc bánh

\(\frac{862}{50} = 17 , 24 g\)