xyOABM

a) Điểm A thuộc tia Ox nên tia OA cũng chính là tia Ox.

Điểm B thuộc tia Oy nên tia OB cũng chính là tia Oy.

Vì hai tia Ox và Oy đối nhau nên hai tia OA và OB đối nhau.

Suy ra điểm O nằm giữa hai điểm A và B.

b) Vì điểm M nằm giữa O và A nên tia OM cũng chính là tia OA.

Mà hai tia OA và OB đối nhau.

Do đó hai tia OM và OB đối nhau.

Suy ra điểm O nằm giữa hai điểm B và M.

c) Điểm O nằm giữa A và B suy ra: AO + OB = AB hay 3 + OB = 6.

Do đó OB = 3 (cm)

Vì OA = 3 cm; OB = 3 cm mà O nằm giữa A và B nên O là trung điểm của đoạn thẳng AB.

Đổi \(25 \%\) = \(\frac{1}{4}\).

Ta có \(28\)m vải còn lại ứng với:

     \(1 - \frac{1}{3} = \frac{2}{3}\) (số mét vải còn lại sau ngày thứ nhất).

Sau ngày thứ nhất người đó bán còn lại số mét vải là:

     \(28 : \frac{2}{3} = 42\) (m)

Số mét vải ban đầu là:

     \(\left(\right. 42 + 15 \left.\right) : \left(\right. 1 - \frac{1}{4} \left.\right) = 57 : \frac{3}{4} = 76\) (m).

a) \(\frac{3}{8} - \frac{1}{6} x\) \(= \frac{1}{4}\)          

Vậy \(x = \frac{3}{4}\).

b) \(\left(\left(\right. x - 1 \left.\right)\right)^{2} = \frac{1}{4}\)                               

\(\left[\right.x=\frac{1}{2}+1x=\frac{- 1}{2}+1\) suy ra \(\left[\right.x=\frac{3}{2}x=\frac{1}{2}\)

Vậy \(x\in{\frac{3}{2};\frac{1}{2}\left.\right.}\).

c) \(\left(\right. x - \frac{- 1}{2} \left.\right) . \left(\right. x + \frac{1}{3} \left.\right) = 0\).

Suy ra \(\left[\right.x-\frac{- 1}{2}=0x+\frac{1}{3}=0\)  hay \(\left[\right.x=\frac{- 1}{2}x=\frac{- 1}{3}\)       

Vậy \(x\in{\frac{- 1}{2};\frac{- 1}{3}\left.\right.}\).

a)a) \(\frac{1}{3} + \frac{3}{4} - \frac{5}{6}\)

\(= \frac{4}{12} + \frac{9}{12} - \frac{10}{12}\)

\(= \frac{4 + 9 - 10}{12}\)

\(= \frac{3}{12}\)

\(= \frac{1}{4}\).

b) \(\frac{- 2}{3} + \frac{6}{5} : \frac{2}{3} - \frac{2}{15}\)

\(= \frac{- 2}{3} + \frac{6}{5} . \frac{3}{2} - \frac{2}{15}\)

\(= \frac{- 2}{3} + \frac{18}{10} - \frac{2}{15}\)

\(= \frac{- 2}{3} + \frac{9}{5} - \frac{2}{15}\)

\(= \frac{- 10}{15} + \frac{27}{15} - \frac{2}{15}\)

\(= \frac{15}{15} = 1\).

c) \(\frac{- 3}{7} + \frac{5}{13} + \frac{- 4}{7}\)

\(= \left(\right. \frac{- 3}{7} + \frac{- 4}{7} \left.\right) + \frac{5}{13}\)

\(= \frac{- 7}{7} + \frac{5}{13}\)

\(= - 1 + \frac{5}{13}\)

\(= \frac{- 8}{13}\).

d) \(\frac{12}{19} + \frac{- 8}{13} - \frac{12}{19} + \frac{5}{- 13} + 2\)

\(= \frac{12}{19} + \frac{- 8}{13} - \frac{12}{19} + \frac{- 5}{13} + 2\)

\(= \left(\right. \frac{12}{19} - \frac{12}{19} \left.\right) + \left(\right. \frac{- 8}{13} + \frac{- 5}{13} \left.\right) + 2\)

\(= 0 + \frac{- 13}{13} + 2\)

\(= 1\).

 \(S = \frac{1}{31} + \frac{1}{32} + \frac{1}{33} + \ldots + \frac{1}{60}\)

\(S < \left(\right. \frac{1}{30} + \frac{1}{30} + \ldots + \frac{1}{30} \left.\right) + \left(\right. \frac{1}{40} + \frac{1}{40} + \ldots + \frac{1}{40} \left.\right) + \left(\right. \frac{1}{50} + \frac{1}{50} + \ldots + \frac{1}{50} \left.\right)\)

\(S < \frac{10}{30} + \frac{10}{40} + \frac{10}{50} < \frac{48}{60} = \frac{4}{5} ;\)

+ \(S > \left(\right. \frac{1}{40} + \frac{1}{40} + \ldots + \frac{1}{40} \left.\right) + \left(\right. \frac{1}{50} + \frac{1}{50} + \ldots + \frac{1}{50} \left.\right) + \left(\right. \frac{1}{60} + \frac{1}{60} + \ldots + \frac{1}{60} \left.\right)\)

\(S > \frac{10}{40} + \frac{10}{50} + \frac{10}{60} > \frac{3}{5} .\)

a) Số lượng bóng rổ bán được trong tháng 1, tháng 2, tháng 3 lần lượt là:

\(15\) quả; \(20\) quả; \(10\) quả.

b) Cả ba tháng cửa hàng bán được:

\(15 + 20 + 10 = 45\) (quả)

c) Tháng 2 cửa hàng bán được nhiều hơn tháng 3:

\(20 – 10 = 10\) (quả)

d) Tỉ số giữa số lượng bóng bán được trong tháng 1 và tháng 2 là:

\(3 : 4 = \frac{3}{4}\)

1. a) \(O\) thuộc các đoạn thẳng: \(AB;CD;OA;OB;OC;OD.\)

b) Ta có \(O\) nằm giữa hai điểm \(A\) và \(B\) và \(OA=OB=3\) cm nên \(O\) là trung điểm của đoạn thẳng \(A B .\)

2. a) Số đo góc \(x O y\) bằng \(3 0^{\circ}\).

b)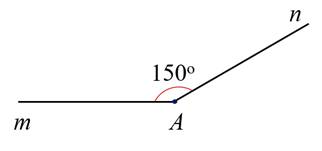 

a) \(\frac{5}{17} - \frac{25}{31} + \frac{12}{17} + \frac{- 6}{31}\)

\(= \frac{5}{17} - \frac{25}{31} + \frac{12}{17} + \frac{- 6}{31}\)

\(= \left(\right. \frac{5}{17} + \frac{12}{17} \left.\right) + \left(\right. - \frac{25}{31} + \frac{- 6}{31} \left.\right)\)

\(= 1 + \left(\right. - 1 \left.\right)\)

\(=0\)

b) \(\frac{17}{8} : \left(\right. \frac{27}{8} + \frac{11}{4} \left.\right)\)

\(= \frac{17}{8} : \left(\right. \frac{27}{8} + \frac{22}{8} \left.\right)\)

\(= \frac{17}{8} : \frac{49}{8}\)

\(= \frac{17}{49}\).

c) \(\frac{1}{5} \cdot \frac{11}{16} + \frac{1}{5} \cdot \frac{5}{16} + \frac{4}{5}\)

\(= \frac{1}{5} \cdot \left(\right. \frac{11}{16} + \frac{5}{16} \left.\right) + \frac{4}{5}\)

\(= \frac{1}{5} \cdot 1 + \frac{4}{5}\)

\(= \frac{1}{5} + \frac{4}{5} = 1.\)

d) \(\frac{5}{6} : 25 - 2 + \frac{- 7}{3} \cdot \frac{2}{7}\)

\(= \frac{5}{6} : 25 - 2 + \frac{- 7}{3} \cdot \frac{2}{7}\)

\(= \frac{5}{6} \cdot \frac{1}{25} - 2 + \frac{- 2}{3}\)

\(= \frac{1}{30} - 2 + \frac{- 2}{3}\)

\(= \frac{1}{30} - \frac{60}{30} + \frac{- 20}{30}\)

\(= \frac{1}{30} - \frac{60}{30} + \frac{- 20}{30} = \frac{- 79}{30}\)

I dream of having a robot named Franky. It's a small home robot. Franky can tidy up rooms, make simple meals, and even water my plants. I want Franky because it can help me with daily chores, so I will have more time to relax and play with my friends. 

Question 1: Robots can work as guards in important places. 

Question 2: Ha Noi is famous for its delicious street food.

Question 3: What type of house will you live in the future?

Question 4: Pack your lunch in a lunch box instead of a plastic bag.