Câu 1: Ngôi kể: Ngôi thứ ba.

Câu 2: Truyện kể về cuộc sống của cha con ông già mù làm nghề bán mai vàng. Cuộc sống dù vất vả nhưng cha con ông rất giàu lòng thương người. Hai cha con đã cưu mang, giúp đỡ một cô gái và sau này cô thành vợ của Mai, con dâu của già Mai. Cuộc sống ngày càng khó khăn, trước mong muốn được thay đổi để cải thiện cuộc sống của con trai, già Mai đồng ý cho các con chặt nửa vườn mai để có vốn đầu tư. Sau đó, dù buồn đau nhưng ông đã dần vui trở lại nhờ sự năng nổ của các con trong công việc mới.

Câu 3: Yếu tố "tình cảm gia đình" trong văn bản có ảnh hưởng sâu sắc đến nhân vật Mai, tạo động lực vượt qua khó khăn, nghèo đói, đồng thời gắn kết các thành viên, giúp họ vượt qua thử thách và tìm được hạnh phúc trong cuộc sống

Câu 4 :Chi tiết ông già Mai đặt bàn tay lên nhát cây mai bị cắt và nghe nhựa mai dính dính nơi bàn tay, rồi âm thầm khóc một mình. Chi tiết này thể hiện tình yêu sâu sắc của ông dành cho vườn mai và nỗi đau khi phải cắt bỏ chúng.

Câu 5 :Yếu tố "tình cảm gia đình" trong văn bản có ảnh hưởng sâu sắc đến nhân vật Mai, tạo động lực vượt qua khó khăn, nghèo đói, đồng thời gắn kết các thành viên, giúp họ vượt qua thử thách và tìm được hạnh phúc trong cuộc sống

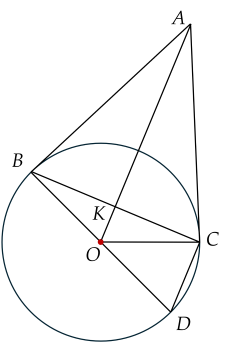
a) Xét tam giác ABCABC có AB=ACAB=AC và AOAO là đường phân giác của góc BACBAC (tính chất hai tiếp tuyến cắt nhau). Do đó AOAO cũng là đường cao, đường trung tuyến của ΔBACΔBAC.

Vậy AOAO vuông góc với BCBC.

b) Ta có BDC^=12CB⌢BDC=21​CB⌢​ (góc nội tiếp)

BOC^= CB⌢BOC= CB⌢​ (góc ở tâm)

Mặt khác BAC^=12BOC^BAC=21​BOC nên BAC^=12CB⌢BAC=21​CB⌢​.

Vậy BAC^=BDC^BAC=BDC, suy ra OA//CDOA//CD (hai góc đồng vị bằng nhau).

c) Xét tam giác ABOABO và tam giác BKOBKO có:

ABO^=BKO^=90∘ABO=BKO=90∘

BOA^BOA: góc chung 

Suy ra ΔABO∼ΔBKOΔABO∼ΔBKO (g.g).

Do đó ta có tỉ số AOBO=BOKOBOAO​=KOBO​ hay OA.OK=OB2=62=36OA.OK=OB2=62=36 (cm).

Xét tam giác vuông ABOABO có: sin⁡BAO^=OBOA=612sinBAO=OAOB​=126​.

Suy ra BAO^=30∘BAO=30∘.

Gọi xx là số máy in mà nhà xuất bản sử dụng (1≤x≤14)(1≤x≤14).

Chi phí lắp đặt là 120x120x (nghìn đồng).

Số giờ để sản xuất đủ số ấn phẩm là: 400030x30x4000​ (giờ).

Chi phí giám sát là: 90.400030x=12000x90.30x4000​=x12000​ (nghìn đồng).

Chi phí sản xuất của nhà sản xuất là: A=120x+12000xA=120x+x12000​ (nghìn đồng).

Áp dụng bất đẳng thức Cauchy, ta có:

A=120x+12000x≥2120x.12000x=2400A=120x+x12000​≥2120x.x12000​​=2400.

Dấu bằng xảy ra khi 120x=12000x120x=x12000​ hay x=10x=10.

Vậy số máy in nhà xuất bản nên sử dụng để chi phí in là nhỏ nhất là 1010 máy.

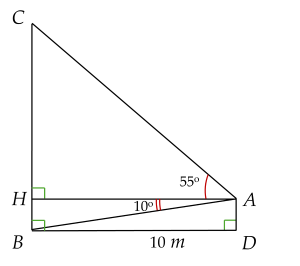
Dựa vào hình vẽ minh họa, ta có: AH=BD=10AH=BD=10 m.

Xét ΔAHBΔAHB vuông tại HH, ta có:

tan⁡BAH^=BHAHtanBAH=AHBH​ (tỉ số lượng giác của góc nhọn)

suy ra BH=AH.tan⁡BAH^=10.tan⁡10∘BH=AH.tanBAH=10.tan10∘ (m).

Xét ΔAHCΔAHC vuông tại HH, ta có:

tan⁡CAH^=CHAHtanCAH=AHCH​ (tỉ số lượng giác của góc nhọn)

suy ra CH=AH.tan⁡CAH^=10.tan⁡55∘CH=AH.tanCAH=10.tan55∘ (m).

Ta có: BC=BH+CH=10.tan⁡10∘+10.tan⁡55∘≈16BC=BH+CH=10.tan10∘+10.tan55∘≈16 m.

Vậy chiều cao của tháp là 1616 m.

Đổi 11 giờ 2525 phút =1712=1217​ giờ; 11 giờ 3030 phút =32=23​ giờ.

Gọi vận tốc riêng của ca nô và vận tốc của dòng nước lần lượt là xx (km/h) và yy (km/h). Điều kiện x>0,y>0,x>yx>0,y>0,x>y.

Trong lần 1

+) Vận tốc xuôi dòng là x+yx+y km/h, quãng đường xuôi dòng là 2020 km nên thời gian xuôi dòng là 20x+yx+y20​ (giờ).

+) Vận tốc ngược dòng là x−yx−y km/h, quãng đường ngược dòng là 1818 km nên thời gian ngược dòng là 18x−yx−y18​ (giờ).

Vì tổng thời gian xuôi dòng và ngược dòng hết 17121217​ giờ nên ta có phương trình

20x+y+18x−y=1712x+y20​+x−y18​=1217​     (1)

Trong lần 2

+) Vận tốc xuôi dòng là x+yx+y (km/h), quãng đường xuôi dòng là 1515 km nên thời gian xuôi dòng là 15x+yx+y15​ (giờ).

+) Vận tốc ngược dòng là x−y(km/h)x−y(km/h), quãng đường ngược dòng là 2424 km nên thời gian ngược dòng là 24x−yx−y24​ (giờ).

Vì tổng thời gian xuôi dòng và ngược dòng hết 3223​ giờ nên ta có phương trình

15x+y+24x−y=32x+y15​+x−y24​=23​    (2)

Từ (1) và (2) ta có hệ phương trình

{20x+y+18x−y=171215x+y+24x−y=32⎩⎨⎧​​x+y20​+x−y18​=1217​x+y15​+x−y24​=23​​

{60x+y+54x−y=17460x+y+96x−y=74⎩⎨⎧​​x+y60​+x−y54​=417​x+y60​+x−y96​=47​​

{60x+y+54x−y=17442x−y=74⎩⎨⎧​​x+y60​+x−y54​=417​x−y42​=47​​

Quy đồng ta được hệ {x+y=30x−y=24{​x+y=30x−y=24​

Giải hệ trên, ta được: {x=27y=3{​x=27y=3​ (thỏa mãn điều kiện).

Vậy vận tốc riêng của ca nô và vận tốc dòng nước lần lượt là 2727 km/h và 33 km/h.

A=(x−5x​+6x​+2​−2−x​x​+3​−x​−3x​+2​):(2−x​+1x​​) 

A=(x+2(x−2)(x−3)−x+32−x−x+2x−3):(2−xx+1)A=((x​−2)(x​−3)x​+2​−2−x​x​+3​−x​−3x​+2​):(2−x​+1x​​) 

A=(x+2(x−2)(x−3)+(x+3)(x−3)(x−2)(x−3)−(x+2)(x−2)(x−3)(x−2)):(2−xx+1)A=((x​−2)(x​−3)x​+2​+(x​−2)(x​−3)(x​+3)(x​−3)​−(x​−3)(x​−2)(x​+2)(x​−2)​):(2−x​+1x​​) 

A=x+2+x−9−x+4(x−2)(x−3):(2−xx+1)A=(x​−2)(x​−3)x​+2+x−9−x+4​:(2−x​+1x​​) 

A=x−3(x−2)(x−3):x+2x+1A=(x​−2)(x​−3)x​−3​:x​+1x​+2​ 

A=1x−2.x+1x+2A=x​−21​.x​+2x​+1​ 

A=x+1x−4A=x−4x​+1​.

b. Tìm các giá trị của x để 1A≤−52A1​≤−25​.

(ĐK: x≥0,x≠4,x≠9x≥0,x=4,x=9)

Để 1A≤−52A1​≤−25​ thì

x−4x+1≤−52x​+1x−4​≤−25​

2x−8≤−5x−52x−8≤−5x​−5

2x+5x−3≤02x+5x​−3≤0

−3≤x≤12−3≤x​≤21​

 0≤x≤12 0≤x​≤21​

 0≤x≤14 0≤x≤41​.

Kết hợp với điều kiện ta được 0≤x≤140≤x≤41​ thì 1A≤−52A1​≤−25​.

​A=2−3​​.(6​+2​)

​​A=2.(2−3)+6.(2−3)​​A=2​.(2−3​​)+6​.(2−3​​)

A=4−23+12−63A=4−23​​+12−63​​

A=1+3−21.3+12−2.33A=1+3−21.3​​+12−2.33​​

A=12−21.3+(3)2+32−2.33+(3)2A=12−21.3​+(3​)2​+32−2.33​+(3​)2​

A=(1−3)2+(3−3)2A=(1−3​)2​+(3−3​)2​

A=3−1+3−3=2A=3​−1+3−3​=2.

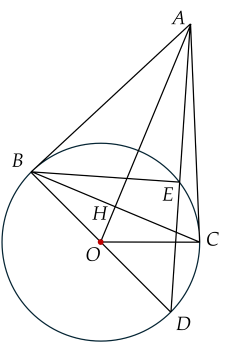
a) Xét đường tròn (O)(O) có: ABAB, ACAC lần lượt là tiếp tuyến tại B,CB,C nên AB=ACAB=AC (tính chất hai tiếp tuyến cắt nhau) .

Suy ra AA thuộc đường trung trực của BCBC.

Mà OB=OC=ROB=OC=R nên OO thuộc đường trung trực của BCBC

Do đó OAOA là đường trung trực của BCBC nên OA⊥ BCOA⊥ BC tại HH.

b) Xét tam giác BEDBED có OEOE là trung tuyến. Mặt khác OE=BD2OE=2BD​ nên tam giác BEDBED vuông tại EE.

Xét ΔABEΔABE và ΔABDΔABD có

BAD^BAD: góc chung

BEA^=DBA^=90∘BEA=DBA=90∘

Suy ra ΔABE∼ΔADBΔABE∼ΔADB (g.g)

Khi đó ABE^=ADB^ABE=ADB (hai góc tương ứng)

và ABAD=AEABADAB​=ABAE​ hay AB2=AD.AEAB2=AD.AE (đpcm).

c) Xét tam giác vuông AOBAOB có:

cos⁡AOB^=OBOA=16+2cosAOB=OAOB​=6​+2​1​.

Suy ra AOB^=75∘AOB=75∘. Do đó BOC^=150∘BOC=150∘.

Khi đó COD^=30∘COD=30∘. 

Diện tích hình quạt giới hạn bởi bán kính OCOC, ODOD và cung nhỏ CDCD là:

S=πR2.30360=πR212S=360πR2.30​=12πR2​ (đvdt).

Vậy diện tích hình quạt giới hạn bởi bán kính OCOC, ODOD và cung nhỏ CDCD là πR21212πR2​ (đvdt).

Gọi xx là số ti vi mà cửa hàng đặt mỗi lần (x∈[1;2500]x∈[1;2500], đơn vị cái).

Số lượng ti vi trung bình gửi trong kho là x22x​ nên chi phí lưu kho tương ứng là 10.x2=5x10.2x​=5x ($)($)

Số lần đặt hàng mỗi năm là 2500xx2500​ và chi phí đặt hàng là:

2500x.(20+9x)x2500​.(20+9x) ($)($)

Khi đó chi phí mà cửa hàng phải trả là:

C(x)=2500x.(20+9x)+5x=5x+50000x+22500C(x)=x2500​.(20+9x)+5x=5x+x50000​+22500

Ta có 5x+50000x≤25x.50000x=10005x+x50000​≤25x.x50000​​=1000.

Suy ra C(x)≤23500C(x)≤23500. Dấu "=""=" xảy ra khi 5x=50000x5x=x50000​, khi đó x=100x=100.

Vậy mỗi năm, cửa hàng nên đặt 100100 cái ti vi để chi phí hàng tồn kho là nhỏ nhất.

a)

Xét ΔABCΔABC vuông tại AA, ta có:

sin⁡B^=ACBC=12320=380sinB=BCAC​=32012​=803​ 

Suy ra B^≈2∘9′B≈2∘9′.

Vậy góc nghiêng là 2∘ 9′2∘ 9′.

b)

Xét ΔABCΔABC vuông tại AA, ta có:

BC=ACsin⁡B^=12sin⁡5∘≈137,7BC=sinBAC​=sin5∘12​≈137,7 km.

Vậy phải bắt đầu cho máy bay hạ cánh khi cách sân bay 137,7137,7 km.