Bạn vào trang cá nhân của mình xem trả lời nhé, tại bài của mình có hình nên nó chưa duyệt.

a) Ta có \(AB^2=\left[\left(-3\right)-\left(-1\right)\right]^2+\left(5-3\right)^2=8\)

Do đó pt đường tròn \(\left(A,AB\right):\left(x+1\right)^2+\left(y-3\right)^2=8\)

b) Pt đường thẳng AB có dạng:

 \(AB:\dfrac{y-3}{5-3}=\dfrac{x+1}{-3+1}\) 

\(\Leftrightarrow\dfrac{y-3}{2}=\dfrac{x+1}{-2}\) 

\(\Leftrightarrow y-3=-x-1\) 

\(\Leftrightarrow x+y-2=0\)

a) \(n\left(\Omega\right)=48\)

Gọi A là biến cố: "Bạn được chọn thích bóng chuyền hoặc bóng bàn."

Áp dụng công thức bù trừ, ta có:

\(n\left(A\right)=19+13-8=24\)

\(\Rightarrow P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{24}{48}=\dfrac{1}{2}\)

b) Xác suất là \(1-\dfrac{1}{2}=\dfrac{1}{2}\)

 Bạn xem lại đề xem là \(0,5.10^9C\) hay là \(0,5.10^{-9}C\) nhé. Thường người ta không cho 2 điện tích độ lớn khủng bố mà lại đặt cách nhau có vài cm như thế đâu.

1) Gọi các số thỏa mãn là \(\overline{abcdef}\)

Số cách chọn vị trí của 3 chữ số 2 là \(C^3_6\)

Số cách chọn vị trí của 2 chữ số 1 là \(C^2_3\)

Số cách chọn 2 chữ số còn lại: \(4^2\)

\(\Rightarrow\) Có tất cả \(C^3_6.C^2_3.4^2=960\) số thỏa ycbt

2) Tập con X bất kì của A muốn thỏa mãn ycbt thì đk cần là phải có ít nhất 1 và nhiều nhất 7 phần tử.

 TH1: \(X=\left\{2\right\}\) -> Có 1 tập X

 TH2: \(X=\left\{2;a_1\right\}\) -> Có \(C^1_6\) tập X

 TH3: \(X=\left\{2;a_1;a_2\right\}\) -> Có \(C^2_6\) tập X

 ...

 TH7: \(X=\left\{2;a_1;...;a_6\right\}\) -> Có \(C^6_6\) tập X

 \(\Rightarrow\) Có tất cả \(1+C^1_6+C^2_6+...+C^6_6=2^6=32\) tập hợp thỏa ycbt.

3) Gọi số thỏa mãn ycbt là \(\overline{abcde}\)

Số cách chọn 2 vị trí của 2 chữ số lẻ liền nhau là 3 cách.

TH1: \(a,b\) lẻ thì có \(P^2_3=6\) cách chọn cặp \(\left(a;b\right)\), bộ \(\left(c;d;e\right)\) có \(P^3_4=24\) cách chọn => Có \(6.24=144\) số

TH2: \(b,c\) lẻ thì cũng có \(P^2_3=6\) cách chọn cặp \(\left(b;c\right)\), còn bộ \(\left(a;d;e\right)\) có \(3.3.2=18\) cách chọn => Có \(6.18=108\) số

TH3: \(c,d\) lẻ thì tương tự TH2, có 108 số.

\(\Rightarrow\) Có tất cả \(144+108+108=360\) số thỏa mãn ycbt.

 Mình gửi đáp án rồi đó nhưng vì có hình nên nó chưa duyệt lên được. Bạn vào trang cá nhân của mình xem nhé.

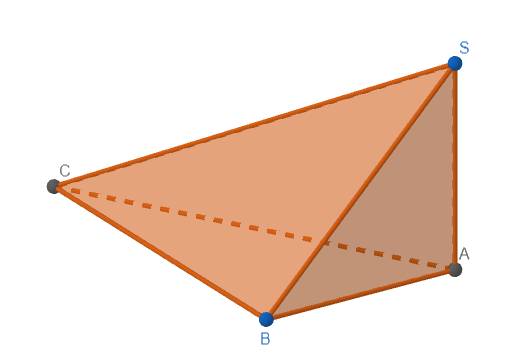
Ta có \(SA\perp\left(ABC\right)\) nên \(SA\perp BC\)

Lại có \(BC\perp AB\) nên \(CB\perp\left(SAB\right)\)

Do đó \(\widehat{SC,\left(SAB\right)}=\widehat{CSB}\)

Mặt khác, \(CB\perp\left(SAB\right)\Rightarrow CB\perp SB\) \(\Rightarrow\Delta SBC\) vuông tại B

Có \(SC=\sqrt{SA^2+AC^2}=\sqrt{a^2+\left(2a\right)^2}=a\sqrt{5}\)

\(CB=AC.\cos30^o=2a.\dfrac{\sqrt{3}}{2}=a\sqrt{3}\)

\(\Rightarrow\sin\widehat{CSB}=\dfrac{CB}{CS}=\dfrac{a\sqrt{3}}{a\sqrt{5}}=\sqrt{\dfrac{3}{5}}\)

\(\Rightarrow\widehat{CSB}=arc\sin\left(\sqrt{\dfrac{3}{5}}\right)\approx50,768^o\)

Vậy \(\widehat{SC,\left(SAB\right)}\approx50,768^o\)

Áp dụng định luật Coulomb, ta có:

\(F=\dfrac{k\left|q_1q_2\right|}{AB^2}\) \(\Rightarrow AB=\sqrt{\dfrac{k\left|q_1q_2\right|}{F}}\) \(=\sqrt{\dfrac{9.10^9\left|4.10^{-8}.4.10^{-8}\right|}{0,4}}\) \(=6.10^{-3}\left(m\right)\)

Vậy \(AB=0,006m\)