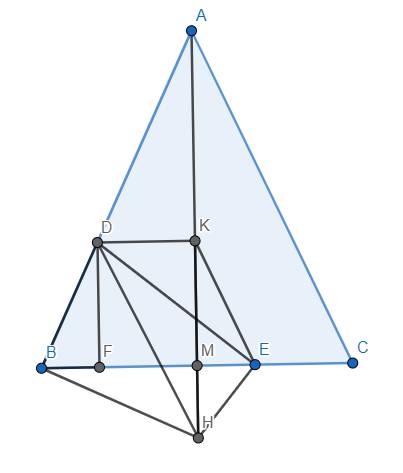
Kẻ trung tuyến AM của tam giác ABC. Qua B kẻ đường thẳng vuông góc với AB cắt AM tại H. Hạ \(DK\perp AM\) tại K. Khi đó H là điểm cố định.

 Vì \(EF=MB=\dfrac{1}{2}BC\) nên \(BF=ME\). Từ đó dễ dàng chứng minh \(\Delta FDB=\Delta MKE\left(c.g.c\right)\) \(\Rightarrow\widehat{DBE}=\widehat{KEB}\). Đồng thời DK//BE nên tứ giác BDKE là hình thang cân \(\Rightarrow\) BDKE là tứ giác nội tiếp.

 Lại có \(\Delta BFD\sim\Delta BMA\) mà \(\Delta BFD=\Delta EMK,\Delta BMA=\Delta CMA\)

 nên \(\Delta EMK\sim\Delta CMA\)

 \(\Rightarrow\widehat{MEK}=\widehat{MCA}\)

 Lại có tứ giác ABHC nội tiếp (do \(\widehat{ABH}=\widehat{ACH}=90^o\)) nên \(\widehat{MCA}=\widehat{BHA}=\widehat{BHK}\)

 Do đó \(\widehat{BEK}=\widehat{BHK}\) \(\Rightarrow\) Tứ giác BHEK nội tiếp.

 Từ đó suy ra 5 điểm B, H, E, K, D cùng thuộc đường tròn (DH). (Trong trường hợp hình vẽ mà \(\widehat{BEK}+\widehat{BHK}=180^o\) thì cũng chứng minh được 5 điểm đó cùng thuộc đường tròn (DH))

 \(\Rightarrow\widehat{DEH}=90^o\)

 \(\Rightarrow\) đường thẳng qua E vuông góc với DE đi qua điểm H cố định. Ta có đpcm.

Vì \(2040⋮24\) nên ta chỉ cần chứng minh \(n^2-1⋮24\)

Do \(n\) là SNT > 3 nên \(n\) có dạng \(6k+1\) hoặc \(6k+5\)

TH1: \(n=6k+1\) thì \(n^2-1\) 

\(=\left(n-1\right)\left(n+1\right)\)

\(=\left(6k+1-1\right)\left(6k+1+1\right)\)

\(=6k\left(6k+2\right)\) 

\(=12k\left(3k+1\right)=A\)

Nếu k chẵn thì hiển nhiên \(A⋮24\). Nếu k lẻ thì \(3k+1⋮2\) \(\Rightarrow A⋮24\)

TH2: \(n=6k+5\)

\(\Rightarrow n^2-1=\left(n-1\right)\left(n+1\right)\)

\(=\left(6k+5-1\right)\left(6k+5+1\right)\)

\(=\left(6k+4\right)\left(6k+6\right)\)

\(=12\left(3k+2\right)\left(k+1\right)=B\)

Xét k lẻ thì \(k+1\) chẵn \(\Rightarrow B⋮24\)

k chẵn thì \(3k+2\) chẵn \(\Rightarrow B⋮24\)

Vậy \(n^2-1⋮24\) \(\Rightarrow n^2-1-2040⋮24\) \(\Rightarrow n^2-2041⋮24\) (đpcm)

Độ cứng của lò xo là \(k=\dfrac{P}{\Delta l}=\dfrac{10m}{0,02}=\dfrac{10.0,02}{0,02}=10\left(N/m\right)\)

Có \(\Delta l'=\dfrac{P}{k}=\dfrac{10m}{200}=\dfrac{10.0,05}{10}=0,05\left(m\right)=5cm\)

\(\Rightarrow l'=20+5=25\left(cm\right)\)

Vậy khi đó chiều dài của lò xo là 25cm.

Mình gửi đáp án rồi nhé, bạn vào trang cá nhân của mình xem.

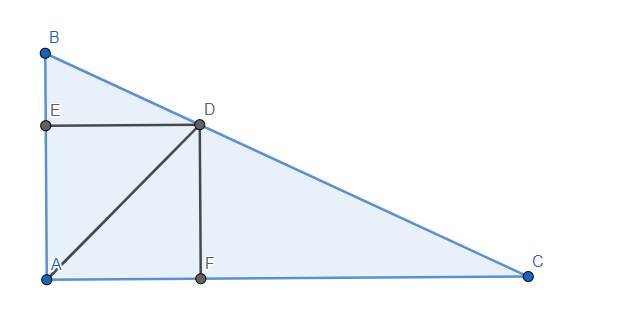
Kẻ DE, DF lần lượt vuông góc với AB, AC tại E, F.

Ta có \(\dfrac{AD^2}{BD^2}=\dfrac{\left(ED\sqrt{2}\right)^2}{BD^2}=\dfrac{2ED^2}{BD^2}=2\left(\dfrac{ED}{BD}\right)^2\) \(=2\left(\dfrac{AC}{BC}\right)^2\)

và \(\dfrac{AD^2}{DC^2}=\dfrac{\left(DF\sqrt{2}\right)^2}{DC^2}=\dfrac{2DF^2}{DC^2}=2\left(\dfrac{DF}{DC}\right)^2=2\left(\dfrac{AB}{BC}\right)^2\)

\(\Rightarrow\dfrac{AD^2}{BD^2}+\dfrac{AD^2}{DC^2}=2\left(\dfrac{AC}{BC}\right)^2+2\left(\dfrac{AB}{BC}\right)^2\) \(=2\left(\dfrac{AB^2+AC^2}{BC^2}\right)\) \(=2\)

\(\Rightarrow\dfrac{1}{BD^2}+\dfrac{1}{CD^2}=\dfrac{2}{AD^2}\), ta có đpcm.

Mình gửi trả lời rồi đó, bạn vào trang cá nhân của mình xem nhé.

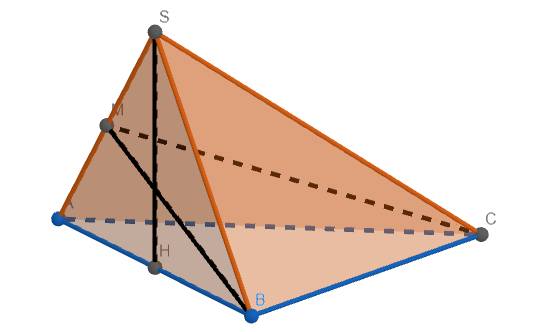
a) Gọi M là trung điểm SA. 

Có \(SH\perp\left(ABC\right)\Rightarrow SH\perp BC\).

Lại có \(BC\perp BA\) \(\Rightarrow BC\perp\left(SAB\right)\) \(\Rightarrow BC\perp SB\)

Do đó \(\widehat{\left(ABC\right),\left(SBC\right)}=\widehat{SBA}=60^o\)

Khi đó tam giác ABC đều \(\Rightarrow AB=BC=SB=SA=4\)

Đồng thời \(MB\perp SA\)

Mặt khác, ta thấy \(\Delta ABC=\Delta SBC\left(c.g.c\right)\) \(\Rightarrow SC=AC\)

\(\Rightarrow\Delta SAC\) cân tại C \(\Rightarrow MC\perp SA\)

Do đó \(\widehat{\left(SAC\right),\left(SAB\right)}=\widehat{BMC}\)

Vì \(BC\perp\left(SAB\right)\Rightarrow BC\perp BM\Rightarrow\Delta BCM\) vuông tại B

\(\Rightarrow\cos\widehat{BMC}=\dfrac{BC}{CM}=\dfrac{4}{\dfrac{4\sqrt{3}}{2}}=\dfrac{2\sqrt{3}}{3}\) 

Vậy \(\cos\widehat{\left(SAC\right),\left(SAB\right)}=\dfrac{2\sqrt{3}}{3}\)

Xét đường tròn (O) có \(\widehat{ACB}=\dfrac{sđ\stackrel\frown{AB}}{2}=\dfrac{\widehat{AOB}}{2}=\dfrac{90^o}{2}=45^o\)

Tam giác ACD vuông tại D có \(\widehat{ACD}=45^o\) nên tam giác ACD vuông cân tại D 

\(\Rightarrow DA=DC\) \(\Rightarrow\) D thuộc trung trực của AC

Mà O cũng thuộc trung trực AC \(\Rightarrow OD\) là trung trực AC 

\(\Rightarrow OD\perp AC\) \(\Rightarrow OD:y=-\dfrac{1}{2}x\)

 Vì đt \(d_1:y=5\perp AC\) và \(A\left(1;-3\right)\) nên phương trình đường thẳng AC có dạng \(AC:x=1\) \(\Rightarrow C\left(1;c\right)\)

 Mà \(C\in d_2:x-2y+1=0\) \(\Rightarrow1-2c+1=0\Leftrightarrow c=1\)

 Vậy \(C\left(1;1\right)\)

 Gọi \(B\left(b;5\right)\) và M là trung điểm AB thì \(M\left(\dfrac{b+1}{2};1\right)\)

 Khi đó vì M thuộc \(d_2:x-2y+1=0\) nên:

 \(\dfrac{b+1}{2}-2.1+1=0\) \(\Leftrightarrow b=1\)

 Vậy A, B, C thẳng hàng (cùng nằm trên đt \(x=1\)). Nên hình ABC không phải là tam giác (đề bài có vấn đề rồi).

 Gọi T là giao điểm của MN và AC. Qua K kẻ đường thẳng song song với AH cắt BC tại S và cắt AN tại R. 

 Ta dễ dàng chứng minh 3 cặp tam giác bằng nhau: 

\(\Delta IAM=\Delta IAK,\Delta IBM=\Delta IBN,\Delta ICN=\Delta ICK\)

 \(\Rightarrow AM=AK,BM=BN,CN=CK\)

 \(\Rightarrow\dfrac{MA}{MB}.\dfrac{NB}{NC}.\dfrac{KC}{KA}=1\)

 Áp dụng định lý Menelaus cho tam giác ABC, cát tuyến MNT, ta có:

 \(\dfrac{MA}{MB}.\dfrac{NB}{NC}.\dfrac{TC}{TA}=1\)

 Do đó \(\dfrac{KC}{KA}=\dfrac{TC}{TA}\) \(\Rightarrow\dfrac{TA}{KA}=\dfrac{TC}{KC}\) (1)

 Áp dụng định lý Thales trong tam giác ANT, ta có:

 \(\dfrac{TA}{KA}=\dfrac{TN}{RK}\) (2)

 Áp dụng định lý Thales trong tam giác CNT, ta có:

 \(\dfrac{TC}{KC}=\dfrac{TN}{KS}\) (3)

 Từ (1), (2) và (3), suy ra \(RK=KS\) (4)

 Áp dụng định lý Thales cho tam giác NKR, ta có:

 \(\dfrac{AE}{RK}=\dfrac{NE}{NK}\) (5)

 Áp dụng định lý Thales cho tam giác NKS, ta có:

 \(\dfrac{EH}{SK}=\dfrac{NE}{NK}\) (6)

 Từ (4), (5) và (6), suy ra \(AE=EH\) \(\Rightarrow\) E là trung điểm AH.

 CMTT \(\Rightarrow\) DE là đường trung bình của tam giác AQH (đpcm)