Theo đề bài, ta có: \(\left\{{}\begin{matrix}n+p+e=34\\p+e-n=10\end{matrix}\right.\)

 \(\Rightarrow2p+2e=44\) \(\Rightarrow p+e=22\)

 Mà \(p=e\Rightarrow2p=2e=22\Rightarrow p=e=11\) \(\Rightarrow n=12\)

 \(\Rightarrow A=Z+n=12+11=33\)

 Vậy số khối \(A=33\)

Xét \(p=2\Rightarrow p+14=16\), không thỏa mãn

Xét \(p=3\Rightarrow\left\{{}\begin{matrix}p+14=17\\2p+5=11\end{matrix}\right.\), thỏa mãn

Xét \(p>3\). Hiển nhiên \(p+14,2p+5>3\). Khi đó:

Nếu \(p\) chia 3 dư 1 thì \(p+14=\left(p-1\right)+15⋮3\), không thỏa mãn

Nếu \(p\) chia 3 dư 2 thì \(2p+5=2p-4+9=2\left(p-2\right)+9⋮3\)  không thỏa mãn.

Vậy, \(p=3\) là số nguyên tố duy nhất thỏa man yêu cầu bài toán.

 Gọi \(ƯCLN\left(2n-1,9n+4\right)=d\left(d\inℕ^∗\right)\)

\(\Rightarrow\left\{{}\begin{matrix}2n-1⋮d\\9n+4⋮d\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}18n-9⋮d\\18n+8⋮d\end{matrix}\right.\)

\(\Rightarrow\left(18n+8\right)-\left(18n-9\right)⋮d\)

\(\Rightarrow17⋮d\)

\(\Rightarrow d=1\) hoặc \(d=17\)

 Ta sẽ chỉ ra có một số tự nhiên \(n\) thỏa mãn \(d=17\). Thật vậy, nếu \(n=9\)  thì \(d=ƯCLN\left(2.9-1;9.9+4\right)=ƯCLN\left(17,85\right)=17\)

 Vậy \(ƯCLN\left(2n-1,9n+4\right)=17\) với \(n\inℕ^∗\)

 Dựng hình bình hành BCDE thì J là trung điểm của BD và CE, đồng thời \(\overrightarrow{CD}=\overrightarrow{BE}\)

 Có \(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AB}+\overrightarrow{BE}=\overrightarrow{AE}\)

 Dễ thấy MN là đường trung bình của tam giác CAE \(\Rightarrow\overrightarrow{AE}=2\overrightarrow{IJ}\)

\(\Rightarrow\overrightarrow{AB}+\overrightarrow{CD}=2\overrightarrow{IJ}\) \(\Rightarrow k=2\)

Gọi \(a=111...11\) (60 chữ số 1)

 \(a=\dfrac{1}{9}.999...99\) (60 chữ số 9)

 \(a=\dfrac{10^{60}-1}{9}\)

 Gọi \(b=222...22\) (30 chữ số 2)

 \(b=\dfrac{2}{9}.999...99\) (30 chữ số 9)

 \(b=\dfrac{2\left(10^{30}-1\right)}{9}=\dfrac{2.10^{30}-2}{9}\)

 Khi đó \(a-b=\dfrac{10^{60}-1}{9}-\dfrac{2.10^{30}-2}{9}\)

 \(=\dfrac{\left(10^{30}\right)^2-2.10^{30}+1}{9}\)

 \(=\dfrac{\left(10^{30}-1\right)^2}{9}\)

 \(=\left(\dfrac{10^{30}-1}{3}\right)^2\)

 Hiển nhiên \(10^{30}-1=999...99\) (30 chữ số 9) chia hết cho 3 nên \(\dfrac{10^{30}-1}{3}\) là số tự nhiên \(\Rightarrow\left(\dfrac{10^{30}-1}{3}\right)^2\) là số chính phương hay \(a-b\) là số chính phương. Ta có đpcm.

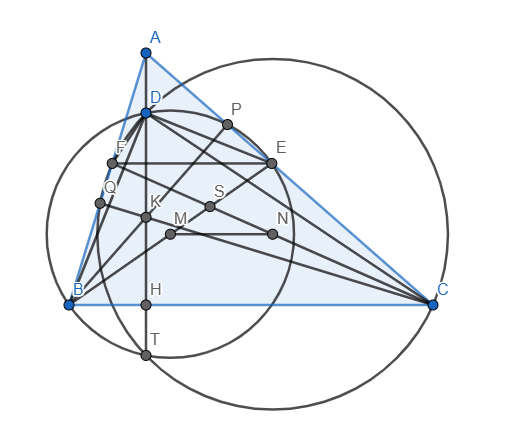
 Gọi M, N lần lượt là trung điểm BE, CF và vẽ các đường tròn đường kính BE, CF (nhận M, N làm tâm). Dễ thấy D là giao điểm của (M) và (N).

 Kẻ hai đường cao BP và CQ cắt nhau tại K. Khi đó K là trực tâm tam giác ABC. Dễ chứng minh \(KB.KP=KC.KQ\) nên \(P_{K/\left(M\right)}=P_{K/\left(M\right)}\)\(\Rightarrow\) K thuộc trục đẳng phương của (M) và (N) hay DK chính là trục đẳng phương của (M) và (N).

 \(\Rightarrow MN\perp DK\).

 Mà \(DK\perp BC\Rightarrow\) MN//BC

 Gọi S là giao điểm của BE và CF. Khi đó ta có \(\dfrac{SN}{NC}=\dfrac{SM}{MB}\) (do MN//BC). Mà \(NC=NF,MB=ME\) nên \(\dfrac{SN}{NF}=\dfrac{SM}{ME}\)

 \(\Leftrightarrow\dfrac{SN}{NF-SN}=\dfrac{SM}{ME-SM}\)  \(\Leftrightarrow\dfrac{SN}{SF}=\dfrac{SM}{SE}\)

 \(\Rightarrow\) MN//EF (đl Thales đảo)

 Do đó EF//BC(//MN), ta có đpcm.

Ta có \(b^2+c^2\le\dfrac{\left(b+c\right)^2}{2}\le\dfrac{\left(4-4a\right)^2}{2}\) (vì \(4-4a>0,b+c>0\) và \(4a+b+c\le4\))

 Hơn nữa, ta có \(4-4a\le b+c\le2\) (do \(b\le c\le1\)) \(\Leftrightarrow a\ge\dfrac{1}{2}\)

 Khi đó \(a^2+b^2+c^2\le a^2+\dfrac{\left(4-4a\right)^2}{2}=a^2+\dfrac{16a^2-32a+16}{2}\) \(=a^2+8a^2-16a+8=9a^2-16a+8\) với \(a\in[\dfrac{1}{2};1)\)

 Xét \(f\left(a\right)=9a^2-16a+8\) trên \([\dfrac{1}{2};1)\)

 Có \(f'\left(a\right)=18a-16\). \(f'\left(a\right)=0\Leftrightarrow a=\dfrac{8}{9}\) (nhận)

 Lập BBT của f(a), dễ thấy \(\max\limits_{[\dfrac{1}{2};1)}f\left(a\right)=\dfrac{9}{4}\) hay \(f\left(a\right)\le\dfrac{9}{4}\) hay \(a^2+b^2+c^2\le\dfrac{9}{4}\)

 Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}b=c\\4a+b+c=4\\a=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=1\\c=1\end{matrix}\right.\)

 Ta có đpcm.

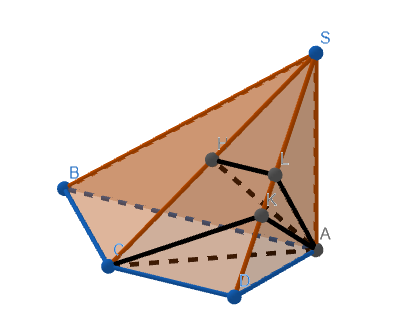
(1) (*) Vì \(SA\perp\left(ABCD\right)\) nên \(\widehat{SB,\left(ABCD\right)}=\widehat{SBA}=arctan\left(\dfrac{SA}{AB}\right)\) \(=arctan\left(\dfrac{a\sqrt{2}}{2a}\right)=arctan\left(\dfrac{\sqrt{2}}{2}\right)\approx35,26^o\)

(*) Ta có \(AC=AD\sqrt{2}=a\sqrt{2}\)  \(\Rightarrow AC=AS\) 

\(\Rightarrow\widehat{SC,\left(ABCD\right)}=\widehat{SCA}=45^o\) (tam giác ACS vuông cân tại A)

(2) (*) Qua H kẻ đường thẳng song song với DC cắt SD tại L. 

Ta có \(SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\) và \(CD\perp DA\)

\(\Rightarrow CD\perp\left(SAD\right)\)

Mà HL//CD \(\Rightarrow HL\perp\left(SAD\right)\)

\(\Rightarrow\widehat{AH,\left(ABCD\right)}=\widehat{HAL}=arcsin\left(\dfrac{HL}{HA}\right)\) \(=arcsin\left(\dfrac{\dfrac{CD}{2}}{\dfrac{SC}{2}}\right)\) \(=arcsin\left(\dfrac{CD}{SC}\right)\) \(=arcsin\left(\dfrac{a}{2a}\right)=arcsin\left(\dfrac{1}{2}\right)=30^o\)

(*) Có \(\dfrac{1}{AK^2}=\dfrac{1}{AD^2}+\dfrac{1}{AS^2}\Rightarrow AK=\dfrac{AD.AS}{\sqrt{AD^2+AS^2}}=\dfrac{a.a\sqrt{2}}{\sqrt{a^2+\left(a\sqrt{2}\right)^2}}=\dfrac{a\sqrt{6}}{3}\)

Có \(CD\perp\left(SAD\right)\Rightarrow CD\perp AK\)

Mà \(AK\perp SD\Rightarrow AK\perp\left(SCD\right)\)

\(\Rightarrow\widehat{AC,\left(SCD\right)}=\widehat{ACK}=arcsin\left(\dfrac{AK}{AC}\right)=arcsin\left(\dfrac{\dfrac{a\sqrt{6}}{3}}{a\sqrt{2}}\right)\) \(=arcsin\left(\dfrac{\sqrt{3}}{3}\right)\) \(\approx35,26^o\)

(3) Ta có \(CB^2+CA^2=\left(a\sqrt{2}\right)^2+\left(a\sqrt{2}\right)^2=4a^2=AB^2\) nên tam giác ABC vuông tại C

 \(\Rightarrow CA\perp CB\)

 Mà \(SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\)

\(\Rightarrow BC\perp\left(SAC\right)\)

\(\Rightarrow\widehat{SB,\left(SAC\right)}=\widehat{BSC}=arctan\left(\dfrac{BC}{CS}\right)=arctan\left(\dfrac{a\sqrt{2}}{2a}\right)\) \(=arctan\left(\dfrac{\sqrt{2}}{2}\right)\approx35,26^o\)