Nếu cái bạn đang nói đến là tích phân thì \(f\left(x\right)|^a_b=f\left(a\right)-f\left(b\right)\). 

 Ví dụ: Tính tích phân \(I=\int\limits^1_02xdx\)

 Giải: \(I=\int\limits^1_02xdx=x^2|^1_0=1^2-0^2=1\)

a) A chia hết cho 3 nhưng không chia hết cho 9 \(\Rightarrow\) A không là số chính phương.

b) \(100!⋮4\) và 7 chia 4 dư 3 nên \(100!+7\) chia 4 dư 3. Do đó nó cũng không phải là SCP.

c) B chia hết cho 11 nhưng không chia hết cho 11² nên B không là SCP.

Điều kiện: \(x\ge2;y\ge-2024;z\ge2025\)

Ta có \(\sqrt{x-2}=\sqrt{1.\left(x-2\right)}\le\dfrac{1+x-2}{2}=\dfrac{x-1}{2}\) (bđt Cô-si)

\(\sqrt{y+2024}=\sqrt{1.\left(y+2024\right)}\le\dfrac{1+y+2024}{2}=\dfrac{y+2025}{2}\)

\(\sqrt{z-2025}=\sqrt{1.\left(z-2025\right)}\le\dfrac{1+z-2025}{2}=\dfrac{z-2024}{2}\)

Cộng theo vế 3 bđt trên, ta có:

\(VP=\sqrt{x-2}+\sqrt{y+2024}+\sqrt{z-2025}\)

\(\le\dfrac{x-1}{2}+\dfrac{y+2025}{2}+\dfrac{z-2024}{2}\)

\(=\dfrac{1}{2}\left(x+y+z\right)=VP\)

Như vậy dấu "=" phải xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x-2=1\\y+2024=1\\z-2025=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-2023\\z=2026\end{matrix}\right.\) (nhận)

Vậy pt đã cho có nghiệm \(\left(x,y,z\right)=\left(3,-2023,2026\right)\)

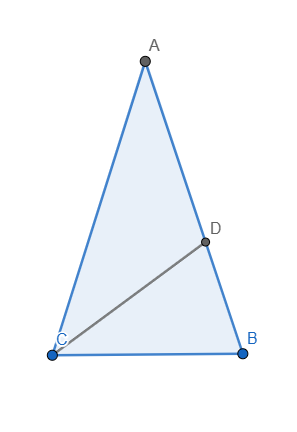
hình bài 2

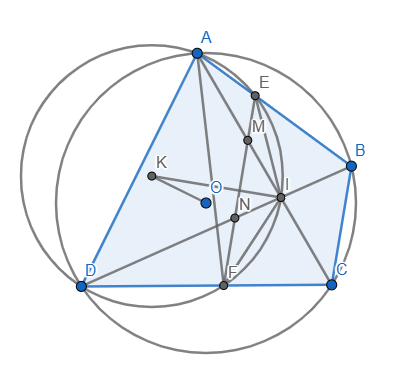
hình bài 1

1)

a) Tứ giác ABCD nội tiếp \(\Rightarrow\widehat{ABC}=180^o-\widehat{ADC}\)

Tứ giác AEFD nội tiếp \(\Rightarrow\widehat{AEF}=180^o-\widehat{ADF}=180^o-\widehat{ADC}\)

\(\Rightarrow\widehat{ABC}=\widehat{AEF}\)

\(\Rightarrow\) EF//BC (2 góc đồng vị bằng nhau)

\(\Rightarrow\widehat{IMN}=\widehat{ICB}\) (2 góc so le trong)

Mà \(\widehat{ICB}=\widehat{ACB}=\widehat{ADB}=\widehat{ADN}\) nên \(\widehat{IMN}=\widehat{ADN}\)

\(\Rightarrow\) Tứ giác AMND nội tiếp (góc ngoài bằng góc trong đối) (đpcm)

b) Tứ giác ABCD nội tiếp \(\Rightarrow\widehat{BAC}=\widehat{BDC}\) hay \(\widehat{EAI}=\widehat{FDI}\)

Lại có \(\widehat{EAI}\) và \(\widehat{FDI}\) là các góc nội tiếp chắn các cung EI, FI của đường tròn (K)

\(\Rightarrow\stackrel\frown{EI}=\stackrel\frown{FI}\Rightarrow EI=FI\)

\(\Rightarrow\) I thuộc trung trực của đoạn EF.

Mà \(KE=KF\Rightarrow\) K cũng thuộc trung trực của đoạn EF

\(\Rightarrow\) IK là trung trực EF \(\Rightarrow IK\perp EF\)

Mà EF//BC (cmt) \(\Rightarrow IK\perp BC\) (đpcm)

2) 

Trên cạnh BC lấy điểm D sao cho tam giác BCD cân tại B. Dễ thấy \(\Delta CBD\sim\Delta CAB\)

\(\Rightarrow\widehat{CBD}=\widehat{BAC}=\widehat{DAB}=36^o\)

\(\Rightarrow\widehat{DBA}=\widehat{CBA}-\widehat{DBC}=72^o-36^o=36^o\)

\(\Rightarrow\widehat{DAB}=\widehat{DBA}\)

\(\Rightarrow\Delta DAB\) cân tại D \(\Rightarrow DA=DB\)

Đặt \(DA=DB=BC=a\), \(CD=b\) \(\left(a>b\right)\)

Khi đó vì \(\Delta CBD\sim\Delta CAB\) nên \(\dfrac{a+b}{a}=\dfrac{a}{b}\) 

\(\Leftrightarrow ab+b^2=a^2\) 

\(\Leftrightarrow-a^2+ab+b^2=0\)

\(\Leftrightarrow-\left(\dfrac{a}{b}\right)^2+\dfrac{a}{b}+1=0\)

\(\Leftrightarrow\dfrac{a}{b}=\dfrac{1+\sqrt{5}}{2}\) (loại nghiệm \(\dfrac{a}{b}=\dfrac{1-\sqrt{5}}{2}\) vì \(\dfrac{a}{b}>1\))

hay \(\dfrac{a+b}{a}=\dfrac{1+\sqrt{5}}{2}\) hay \(\dfrac{AB}{BC}=\dfrac{1+\sqrt{5}}{2}\)

\(N=\dfrac{x^2+x+1}{x^2+1}\)

\(\Leftrightarrow\left(x^2+1\right)N=x^2+x+1\)

\(\Leftrightarrow Nx^2+N=x^2+x+1\)

\(\Leftrightarrow\left(N-1\right)x^2-x+N-1=0\) (*)

Có \(\Delta=\left(-1\right)^2-4\left(N-1\right)^2\) 

\(=1-\left(2N-2\right)^2\)

\(=\left(1+2N-2\right)\left(1-2N+2\right)\)

\(=\left(2N-1\right)\left(3-2N\right)\)

Để (*) có nghiệm thì \(\Delta=\left(2N-1\right)\left(3-2N\right)\ge0\)

\(\Leftrightarrow\dfrac{1}{2}\le N\le\dfrac{3}{2}\)

\(N=\dfrac{1}{2}\) khi \(x=-\dfrac{-1}{2\left(N-1\right)}=\dfrac{1}{2\left(\dfrac{1}{2}-1\right)}=-1\)

\(N=\dfrac{3}{2}\) khi \(x=-\dfrac{-1}{2\left(N-1\right)}=\dfrac{1}{2\left(\dfrac{3}{2}-1\right)}=1\)

Vậy \(minN=\dfrac{1}{2}\) khi \(x=-1\) và \(maxN=\dfrac{3}{2}\) khi \(x=1\)

\(Q=mc\Delta t=5.3870.\left(50-20\right)=580500\left(J\right)\)

 Có tất cả \(A^2_{30}=870\) véc-tơ thỏa mãn yêu cầu bài toán (chọn ra 2 đỉnh trong 30 đỉnh sau đó chọn ra 1 điểm gốc và 1 điểm cuối)

Xét \(p=2\) thì \(p^2+6=10\) là hợp số, không thỏa mãn

Xét \(p=3\) thì \(p^2+6=15\) là hợp số, không thỏa mãn.

Xét \(p>3\) thì \(p^2-7>2\) và \(p^2-7⋮2\) nên là hợp số, không thỏa mãn.

Vậy không có số nguyên tố \(p\) nào thỏa mãn yêu cầu đề bài.