

Nguyễn Khánh Ngọc
Giới thiệu về bản thân
Chào mừng bạn đến với trang cá nhân của Nguyễn Khánh Ngọc





0





0





0





0





0





0





0
2024-12-07 20:34:40
a) vuông cân nên
vuông tại có
Suy ra nên .
Vậy vuông cân tại
b) Chứng minh tương tự câu a ta được vuông cân tại nên và
Mặt khác suy ra và // (cùng vuông góc với
Tứ giác có // nên là hình bình hành.
Hình bình hành có một góc vuông nên là hình chữ nhật
Hình chữ nhật có hai cạnh kề bằng nhau nên là hình vuông.
2024-12-07 20:34:12
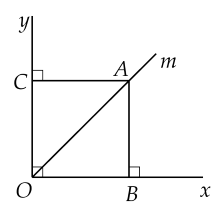
Tứ giác có ba góc vuông
Nên là hình chữ nhật.
Mà nằm trên tia phân giác suy ra .
Khi đó là hình vuông.
2023-10-02 15:06:56
2023-10-02 15:05:56
2023-10-02 15:05:41
2023-10-02 15:04:22
2023-10-02 15:04:10
2023-10-02 15:03:49
2023-10-02 15:02:24
2023-10-02 15:01:57