

when the imposter is sus
Giới thiệu về bản thân



































Ta có: \(x^2+2x^2+15=3x^2+15\)
Thực hiện phép chia, ta được:
Suy ra để \(x^2+2x^2+15\) chia hết cho x + 3 thì - (9 - y)x + (15 - 3y) = 0
Hay - (9 - y)x = 15 - 3y
Khi đó \(x=\dfrac{15-3y}{-9+y}\) hay \(\left(15-3y\right)⋮\left(-9+y\right)\)
Hay \(\left[\left(15-3y\right)-3\left(-9+y\right)\right]⋮\left(-9+y\right)\)
Hay \(42⋮\left(-9+y\right)\)
Khi đó (-9 + y) ϵ Ư(42) = {1; -1; 2; -2; 3; -3; 6; -6; 7; -7; 14; -14; 21; -21; 42; -42}
Xét bảng
| -9 + y | 1 | -1 | 2 | -2 | 3 | -3 | 6 | -6 | 7 | -7 | 14 | -14 | 21 | -21 | 42 | -42 |
| y | 10 | 8 | 11 | 7 | 12 | 6 | 15 | 3 | 16 | 2 | 23 | -5 | 30 | -12 | 51 | -33 |
| \(x=\dfrac{15-3y}{-9+y}\) | -15 | 9 | -9 | 3 | -7 | 1 | -5 | -1 |
-33/7 (loại) |
-9/7 (loại) | -27/7 (loại) | -15/7 (loại) | -25/7 (loại) | -17/7 (loại) | -23/7 (loại) | -19/7 (loại) |
Vậy để \(x^2+2x^2+15\) chia hết cho x + 3 thì x ϵ {-15; 9; -9; 3; -7; 1; -5; -1}
Gọi X là tập hợp các kết quả có thể xảy ra.
Ta có \(X=\left\{\left(1;1\right);\left(1;2\right);\left(1;3\right);...;\left(6;6\right)\right\}\). Ta thấy tập hợp trên có 36 phần tử, hoặc 36 kết quả có thể xảy ra.
a) Biến cố trên có thể xảy ra nếu xảy ra 1 trong các kết quả sau:
(4;6); (5;5); (6;4). Có 3 kết quả để biến cố trên xảy ra.
Vậy xác suất của biến cố trên là \(\dfrac{3}{36}=\dfrac{1}{12}\).
b) Biến cố trên có thể xảy ra nếu xảy ra 1 trong các kết quả sau:
(1;2); (2;1); (1;4); (2;3); (3;2); (4;1); (1;6); (2;5); (3;4); (4;3); (5;2); (6;1); (3;6); (4;5); (5;4); (6;3); (5;6); (6;5). Có 18 kết quả để biến cố trên xảy ra.
Vậy xác suất để biến cố trên xảy ra là \(\dfrac{18}{36}=\dfrac{1}{2}\).
TH1: x ≥ 0
Khi đó \(\left|x+1\right|+\left|x+2\right|+\left|x+2020\right|=x+1+x+2+x+2020\)
\(=3x+2023=4x\)
Suy ra \(4x-3x=x=2023\) (thỏa mãn điều kiện)
TH2: x < 0
Khi đó 4x < 0 hay vế phải luôn là một số âm. Tuy nhiên vế trái luôn luôn có giá trị lớn hơn 0 nên luôn là 0 hoặc là một số dương, suy ra vô lí.
Tóm lại, x = 2023.
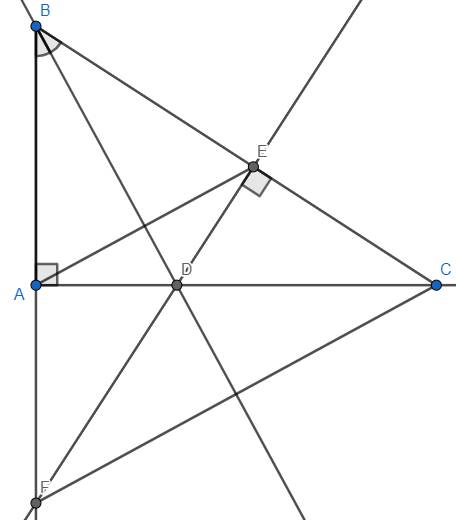
c) Ta đã biết DA = DE (chứng minh trên) (1)
Trong tam giác EDC vuông tại E có DC đối diện đỉnh E
Suy ra DC là cạnh lớn nhất trong tam giác EDC
Hay DC > DE (2)
Từ (1) và (2) suy ra DC > AD hay AD < DC
Gọi x, y, z (học sinh) lần lượt là số học sinh hạnh kiểm tốt, khá, đạt của lớp 7A.
Theo đề ta có \(\dfrac{1}{2}y=\dfrac{3}{4}x=\dfrac{2}{5}z\Leftrightarrow\dfrac{y}{2}=\dfrac{x}{\dfrac{4}{3}}=\dfrac{z}{\dfrac{5}{2}}\) và y - x = 4.
Từ tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{y}{2}=\dfrac{x}{\dfrac{4}{3}}=\dfrac{z}{\dfrac{5}{2}}=\dfrac{y-x}{2-\dfrac{4}{3}}=\dfrac{4}{\dfrac{2}{3}}=6\)
Suy ra \(x=6\cdot\dfrac{4}{3}=8;y=6\cdot2=12;z=6\cdot\dfrac{5}{2}=15\)
Vậy số học sinh có hạnh kiểm tốt, khá, đạt của lớp 7A lần lượt là 8 học sinh, 12 học sinh và 15 học sinh.
Vì biểu thức trên tự chứa chính mình (\(\sqrt{x+\sqrt{x+\sqrt{x+\sqrt{...}}}}=2\))
Suy ra \(\sqrt{x+\sqrt{x+\sqrt{x+\sqrt{...}}}}=\sqrt{x+\sqrt{2}}=2\)
\(x+\sqrt{2}=2^2=4\)
\(x=4-\sqrt{2}\)
Vậy \(x=4-\sqrt{2}\)
a)
\(A=\left(x+1\right)\left(x-1\right)+\left(3x-1\right)\left(x-2\right)+3x\)
\(A=x^2+x-x-1+3x^2-6x-x+2+3x\)
\(A=\left(x^2+3x^2\right)+\left(x-x-6x-x+3x\right)+\left(-1+2\right)\)
\(A=4x^2-4x+1\)
b) \(A\left(-4,5\right)=4\cdot\left(-4,5\right)^2-4\cdot\left(-4,5\right)+1=100\)
c)
Vậy A:B = 2x + 1, Q = 2x + 1 và R = 0.
d) Vì A chia hết cho B nên tất cả giá trị nguyên của x đều thỏa mãn để giá trị của đa thức A chia hết cho giá trị của đa thức B.
\(\dfrac{3^{10}\cdot11+9^5\cdot5}{27^3\cdot2^4}\cdot x=-9\)
\(\dfrac{3^{10}\cdot11+3^{10}\cdot5}{3^9\cdot2^4}\cdot x=-9\)
\(\dfrac{3\cdot3^9\cdot16}{3^9\cdot16}\cdot x=-9\)
3x = -9
\(x=-\dfrac{9}{3}=-3\)
\(\dfrac{3\cdot3^9\cdot\left(11+5\right)}{3^9\cdot16}\cdot x=-9\)
a) Ta có:
\(f\left(x\right)=2x^3-x^5+3x^4+x^2-\dfrac{1}{2}x^3+3x^5-2x^2-x^4+1\)
\(f\left(x\right)=\left(-x^5+3x^5\right)+\left(3x^4-x^4\right)+\left(2x^3-\dfrac{1}{2}x^3\right)+\left(x^2-2x^2\right)+1\)
\(f\left(x\right)=2x^5+2x^4+\dfrac{3}{2}x^3-x^2+1\)
Sắp xếp đa thức f(x) the lũy thừa giảm dần của biến, ta được:
\(f\left(x\right)=2x^5+2x^4+\dfrac{3}{2}x^3-x^2+1\)
b) Bậc của đa thức f(x) là 5
c) Ta có:
\(f\left(1\right)=2\cdot1^5+2\cdot1^4+\dfrac{3}{2}\cdot1^3-1^2+1=5,5\) . Vậy f(1) = 5,5.
\(f\left(-1\right)=2\cdot\left(-1\right)^5+2\cdot\left(-1\right)^4+\dfrac{3}{2}\cdot\left(-1\right)^3-\left(-1\right)^2+1=-1,5\). Vậy f(-1) = -1,5.
a) Vì x và y là hai đại lượng tỉ lệ thuận nên \(a=\dfrac{x}{y}=\dfrac{6}{2}=3\)
b) Từ câu a ta có x = 3y, suy ra \(y=\dfrac{1}{3}x\)
c) Khi x = 3 thì \(y=\dfrac{1}{3}\cdot3=1\)