

when the imposter is sus
Giới thiệu về bản thân



































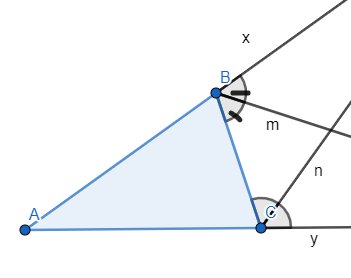
a) Giả sử Bm // Cn. Khi đó ta có:
\(\widehat{xBm}=\widehat{BCn}\) (hai góc đồng vị) và \(\widehat{BCn}+\widehat{CBm}=180^o\) (hai góc trong cùng phía)
\(\Rightarrow\widehat{xBm}+\widehat{mBC}=\widehat{xBC}=180^o\) (a)
Mà \(\widehat{ABC}\) và \(\widehat{xBC}\) là hai góc kề bù (vì \(\widehat{xBC}\) là góc ngoài đỉnh B)
\(\Rightarrow\widehat{ABC}+\widehat{mBC}=180^o\)
\(\Rightarrow\widehat{mBC}=180^o-\widehat{ABC}\)
\(\Rightarrow\widehat{mBC}< 180^o\) (b)
Từ (a) và (b) suy ra vô lí, suy ra Bm không song song với Cn
Vậy Bm cắt Cn
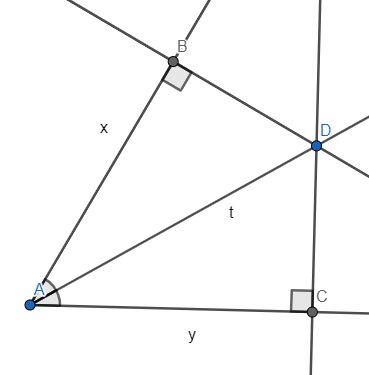
Vì At là tia phân giác của \(\widehat{xAy}\) nên \(\widehat{BAD}=\widehat{CAD}\)
Xét ΔBAD vuông tại B và ΔCAD vuông tại C có:
- AD là cạnh chung
- \(\widehat{BAD}=\widehat{CAD}\) (chứng minh trên)
Suy ra ΔBAD = ΔCAD (cạnh huyền - góc nhọn), từ đó AB = AC (vì hai cạnh tương ứng)
| Cấu tạo | CTHH | KLPT |
| Sulfur (VI) & Oxygen | SO3 | 80u |
| Barium (II) & Sulfur (II) | BaS | 169u |
| Aluminium (III) & SO4 (II) | Al2(SO4)3 | 342u |
| Silver (I) & NO3 (I) | AgNO3 | 170u |
| Potassium (I) & Chlorine (I) | KCl | 74.5u |
| Sodium (I) & Oxygen | Na2O | 62u |
| Calcium (II) & CO3 (II) | CaCO3 | 100u |
\(\dfrac{72^3\cdot54^2}{108^4}=\dfrac{\left(2^3\cdot3^2\right)^3\cdot\left(2\cdot3^3\right)^2}{\left(2^2\cdot3^3\right)^4}=\dfrac{2^9\cdot3^6\cdot2^2\cdot3^6}{2^8\cdot3^{12}}\)
\(=\dfrac{2^{11}\cdot3^{12}}{2^8\cdot3^{12}}=2^3=8\)
\(\dfrac{3}{5}+\dfrac{3}{11}-\left(-\dfrac{3}{7}\right)+\left(-\dfrac{2}{97}\right)-\dfrac{1}{35}-\dfrac{3}{4}+\left(-\dfrac{23}{44}\right)\)
\(=\left(\dfrac{3}{5}+\dfrac{3}{7}-\dfrac{1}{35}\right)+\left(\dfrac{3}{11}-\dfrac{3}{4}-\dfrac{23}{44}\right)-\dfrac{2}{97}\)
\(=1-1-\dfrac{2}{97}=-\dfrac{2}{97}\)
\(x^2⋮6\) ⇒ \(x^2\in\left\{0;36;144;324;...\right\}\)
⇒ \(x\in\left\{0;6;12;18;...\right\}\) ⇒ \(x⋮6\)
Vậy mệnh đề trên là mệnh đề đúng.
Đặt \(A=\dfrac{1}{3}+\dfrac{1}{3^3}+\dfrac{1}{3^5}+...+\dfrac{1}{3^{47}}+\dfrac{1}{3^{49}}+\dfrac{1}{3^{51}}\)
Và \(B=\dfrac{1}{3^2}+\dfrac{1}{3^4}+\dfrac{1}{3^6}+...+\dfrac{1}{3^{46}}+\dfrac{1}{3^{48}}+\dfrac{1}{3^{50}}\)
Ta có:
\(9A=3+\dfrac{1}{3}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{45}}+\dfrac{1}{3^{47}}+\dfrac{1}{3^{49}}\)
\(9A-A=\left(3+\dfrac{1}{3}+...+\dfrac{1}{3^{47}}+\dfrac{1}{3^{49}}\right)-\left(\dfrac{1}{3}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{49}}+\dfrac{1}{3^{51}}\right)\)
\(8A=3-\dfrac{1}{3^{51}}\)
\(A=\dfrac{3-\dfrac{1}{3^{51}}}{8}\)
\(9B=1+\dfrac{1}{3^2}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{44}}+\dfrac{1}{3^{46}}+\dfrac{1}{3^{48}}\)
\(9B-B=\left(1+\dfrac{1}{3^2}+...+\dfrac{1}{3^{46}}+\dfrac{1}{3^{48}}\right)-\left(\dfrac{1}{3^2}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{48}}+\dfrac{1}{3^{50}}\right)\)
\(8B=1-\dfrac{1}{3^{50}}\)
\(B=\dfrac{1-\dfrac{1}{3^{50}}}{8}\)
Suy ra
\(-\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{50}}-\dfrac{1}{3^{51}}=B-A=\dfrac{1-\dfrac{1}{3^{50}}}{8}-\dfrac{3-\dfrac{1}{3^{51}}}{8}\)
\(=\dfrac{\left(1-\dfrac{1}{3^{50}}\right)-\left(3-\dfrac{1}{3^{51}}\right)}{8}=\dfrac{-2-\dfrac{1}{3^{50}}+\dfrac{1}{3^{51}}}{8}=\dfrac{-2+\dfrac{-3^{51}+3^{50}}{3^{101}}}{8}\)
\(=\dfrac{-2+\dfrac{3^{50}\left(-3+1\right)}{3^{101}}}{8}=\dfrac{-2-\dfrac{2}{3^{51}}}{8}=-\dfrac{2\left(1+\dfrac{1}{3^{51}}\right)}{8}=-\dfrac{1+\dfrac{1}{3^{51}}}{4}\)
b) Ta có:
P(x) + H(x) = x4 - x3 + 2x2 + x + 1
=> H(x) = x4 - x3 + 2x2 + x + 1 - P(x)
=> H(x) = (x4 - x3 + 2x2 + x + 1) - (2x4 - x2 + x - 2)
=> H(x) = -x4 - x3 + 3x2 + 3
Vậy H(x) = -x4 - x3 + 3x2 + 3
\(\left(x^2-1\right)\left(x^2-5\right)< 0\)
\(\Rightarrow\left\{{}\begin{matrix}x^2-1< 0\\x^2-5>0\end{matrix}\right.\) hoặc \(\left\{{}\begin{matrix}x^2-1>0\\x^2-5< 0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x^2< 1\\x^2>5\end{matrix}\right.\)(vô lí) hoặc \(\left\{{}\begin{matrix}x^2>1\\x^2< 5\end{matrix}\right.\)
\(\Rightarrow1< x< \sqrt{5}\) hoặc \(-\sqrt{5}< x< -1\)
Vậy \(-\sqrt{5}< x< -1\) hoặc \(1< x< \sqrt{5}\)
Trước hết ta phải chứng minh \(\dfrac{a}{b}< \dfrac{a+1}{b+1}\) (a, b ϵ N; a < b).
Thật vậy, \(\dfrac{a}{b}=\dfrac{a\left(b+1\right)}{b\left(b+1\right)}=\dfrac{a+ab}{b^2+b}\) và \(\dfrac{a+1}{b+1}=\dfrac{\left(a+1\right)b}{\left(b+1\right)b}=\dfrac{ab+b}{b^2+b}\).
Mà theo giả thuyết là a < b nên \(\dfrac{a+ab}{b^2+b}< \dfrac{ab+b}{b^2+b}\), suy ra \(\dfrac{a}{b}< \dfrac{a+1}{b+1}\) (a, b ϵ N; a < b).
Từ đây ta có:
\(B=\dfrac{2022^{2022}+1}{2022^{2023}+1}=\dfrac{2022^{2023}+2022}{2022^{2024}+2022}=\dfrac{2022^{2023}+2021+1}{2022^{2024}+2021+1}\)
Đặt \(A_1=\dfrac{2022^{2023}+2}{2022^{2024}+2}=\dfrac{2022^{2023}+1+1}{2022^{2024}+1+1}\), rõ ràng \(A_1>A\).
Đặt \(A_2=\dfrac{2022^{2023}+3}{2022^{2024}+3}=\dfrac{2022^{2023}+2+1}{2022^{2024}+2+1}\), rõ ràng \(A_2>A_1\).
...
Đặt \(A_{2020}=\dfrac{2022^{2023}+2021}{2022^{2024}+2021}=\dfrac{2022^{2023}+2020+1}{2022^{2024}+2020+1}\), rõ ràng \(A_{2020}>A_{2019}\) và \(B>A_{2020}\).
Suy ra \(B>A_{2020}>A_{2019}>...>A_2>A_1>A\). Vậy A < B.