Đặt \(x=\dfrac{1}{49\cdot44}+\dfrac{1}{44\cdot39}+...+\dfrac{1}{14\cdot9}+\dfrac{1}{9\cdot4}\) và y = ... (thừa số thứ hai chưa ghi rõ, nếu ghi rõ thì mới làm được)

Ta có:

\(5x=5\left(\dfrac{1}{49\cdot44}+\dfrac{1}{44\cdot39}+...+\dfrac{1}{14\cdot9}+\dfrac{1}{9\cdot4}\right)\)

\(5x=\dfrac{5}{49\cdot44}+\dfrac{5}{44\cdot39}+...+\dfrac{5}{14\cdot9}+\dfrac{5}{9\cdot4}\)

\(5x=\dfrac{1}{4}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{14}+...+\dfrac{1}{39}-\dfrac{1}{44}+\dfrac{1}{44}-\dfrac{1}{49}\)

\(5x=\dfrac{1}{4}-\dfrac{1}{49}=\dfrac{45}{196}\)

\(x=\dfrac{45}{196}\div5=\dfrac{9}{196}\)

Từ đây tự tìm y (thừa số thứ hai)

Suy ra \(A=xy=\dfrac{9}{196}\cdot...=...\)

Theo đề ta có y = ax, x = bz. Suy ra y = ax = abz.

Vậy y tỉ lệ thuận với z theo hệ số tỉ lệ ab

Để x là số nguyên thì 3a - 2 ϵ Ư(2) = {1; -1; 2; -2}.

Lập bảng

a) Để x là số nguyên dương thì 3a - 2 phải là số nguyên dương. Vậy để x là số nguyên dương thì a = 1.

b) Để x là số nguyên âm thì 3a - 2 phải là số nguyên âm. Vậy để x là số nguyên âm thì a = 0.

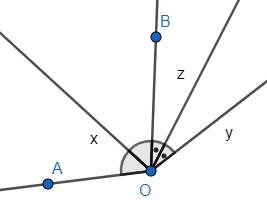
Gọi Oz là tia phân giác của \(\widehat{BOy}\). Ta có:

\(\widehat{AOy}+\widehat{BOy}=\widehat{AOB}+2\widehat{BOy}=2\widehat{xOB}+4\widehat{BOz}=2\widehat{xOB}+2\widehat{BOy}=2\widehat{xOy}\)

Khi đó \(\widehat{xOy}=\dfrac{\widehat{AOy}+\widehat{BOy}}{2}\)

c)

2x(3x - 1) - 3x(5 + 2x) = 0

x[2(3x - 1)] - x[3(5 + 2x)] = 0

x(6x - 2 - 15 - 6x) = 0

-17x = 0

x = 0

Vậy x = 0

Để biểu thức trên đúng thì cả x - 1 và x - 2 đều cùng dấu (dương hoặc âm).

Suy ra \(\left(x-1\right)\left(x-2\right)>0\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x-1>0\\x-2>0\end{matrix}\right.\\\left[{}\begin{matrix}x-1< 0\\x-2< 0\end{matrix}\right.\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x>1\\x>2\end{matrix}\right.\\\left[{}\begin{matrix}x< -1\\x< -2\end{matrix}\right.\end{matrix}\right.\)

Vậy x < 1; 2 < x

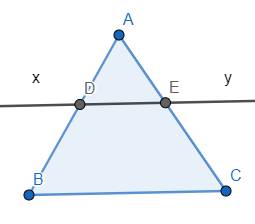
Dễ dàng thấy được \(\widehat{ABC}=\widehat{ADE}\) và \(\widehat{ACB}=\widehat{AED}\) (vì với mỗi cặp thì hai góc của cặp đó là hai góc so le trong)

Vì \(\widehat{ADE}\) và \(\widehat{BDE}\) là hai góc kề bù nên \(\widehat{ADE}+\widehat{BDE}=180^o\)

Mà \(\widehat{ABC}=\widehat{ADE}\) nên \(\widehat{ABC}+\widehat{BDE}=180^o\), suy ra \(\widehat{ABC}\) và \(\widehat{BDE}\) là hai góc bù nhau.

Suy luận tương tự như trên, ta được \(\widehat{ACB}\) và \(\widehat{CED}\) là hai góc bù nhau.

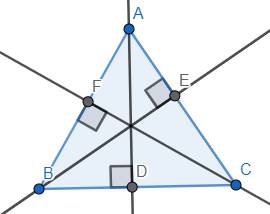
Nhận xét: AD, BE và CF là các đường cao, chúng đồng quy tại một điểm.

c) Tương tự như câu d), trước hết phải chứng minh \(\left(\dfrac{a+b}{c+d}\right)^2=\dfrac{a^2+b^2}{c^2+d^2}\)

Từ đó suy ra \(\dfrac{\left(a+b\right)^2}{\left(c+d\right)^2}=\dfrac{a^2+b^2}{c^2+d^2}\) \(\Rightarrow\dfrac{\left(a+b\right)^2}{a^2+b^2}=\dfrac{\left(c+d\right)^2}{c^2+d^2}\)

d) Từ \(\dfrac{a}{b}=\dfrac{c}{d}\) suy ra \(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}=k\)

\(\Rightarrow\left(\dfrac{a+b}{c+d}\right)^3=k^3\) (1)

Mặt khác, \(\dfrac{a}{c}=\dfrac{b}{d}=k\) \(\Rightarrow\left(\dfrac{a}{c}\right)^3=\left(\dfrac{b}{d}\right)^3=\dfrac{a^3}{c^3}=\dfrac{b^3}{d^3}=\dfrac{a^3+b^3}{c^3+d^3}=k^3\) (2)

Từ (1) và (2) \(\Rightarrow\left(\dfrac{a+b}{c+d}\right)^3=\dfrac{a^3+b^3}{c^3+d^3}\)