

when the imposter is sus
Giới thiệu về bản thân



































(Đề ghi không rõ lắm, nên câu b có thể làm sai đề)
\(\dfrac{-75}{x+6}=-15\)
\(x+6=\dfrac{-75}{-15}=5\)
\(x=5-6=-1\)
\(-25-5x\left(x+2\right)=50\)
\(5x\left(x+2\right)=-25-50=-75\)
\(x\left(x+2\right)=x^2+2x=\dfrac{-75}{5}=-15\)
\(x^2+2x+1=-15+1=-14\)
\(\left(x+1\right)^2=-14\)
Suy ra không có nghiệm, vì không có căn bậc hai của số âm

Giả sử a//BC. Theo đề ta có:
\(\widehat{A_1}=\widehat{C_1}\) (hai góc so le trong) (1)
\(\widehat{A_1}=\dfrac{1}{2}\widehat{ABC}+\widehat{BAC}\) (vì BD là tia phân giác của \(\widehat{ABC}\)) (2)
\(\widehat{C_1}=\widehat{ABC}+\widehat{BAC}\) (vì \(\widehat{C_1}\) là góc ngoài của \(\widehat{C}\) ) (3)
Từ (1); (2) và (3) suy ra \(\dfrac{1}{2}\widehat{ABC}=\widehat{ABC}\), hay \(\dfrac{1}{2}=1\) (vô lí)
Suy ra a không song song với BC, hay a cắt đường thẳng BC
a . bcd . abc = abcabc
(a . bcd) . abc = abc . 1001
a . bcd = 1001
Phân tích 1001 thành tích các thừa số nguyên tố: 1001 = 7 . 11 . 13
Suy ra a = 7; bcd = 11 . 13 = 143
Vậy a = 7; b = 1; c = 4; d = 3
\(\left[-\sqrt{2,25}+4\sqrt{\left(-2,15\right)^2}-\left(3\sqrt{\dfrac{7}{6}}\right)^2\right]\sqrt{1\dfrac{9}{16}}\)
\(=\left[-1,5+4\sqrt{2,15^2}-9\cdot\dfrac{7}{6}\right]\sqrt{\dfrac{25}{16}}\)
\(=\left[4\cdot\dfrac{43}{20}-10,5-1,5\right]\cdot\dfrac{5}{4}\)
\(=\left[\dfrac{43}{5}-12\right]\cdot\dfrac{5}{4}\)
\(=\dfrac{43}{5}\cdot\dfrac{5}{4}-12\cdot\dfrac{5}{4}\)
\(=\dfrac{43}{4}-15=\dfrac{-17}{4}\)
Nếu làm riêng thì:
- Người thứ nhất làm được \(\dfrac{1}{4}\) công việc mỗi giờ
- Người thứ hai làm được \(\dfrac{1}{6}\) công việc mỗi giờ
Khi đó nếu cả hai làm chung trong 45 phút (hay \(\dfrac{3}{4}\) giờ) thì hai người làm được \(\left(\dfrac{1}{4}+\dfrac{1}{6}\right)\cdot\dfrac{3}{4}=\dfrac{5}{16}\) công việc
a) Lập bảng
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... |
| 7n | 7 | 9 | 3 | 1 | 7 | 9 | 3 | 1 | ... |
| 9n | 9 | 1 | 9 | 1 | 9 | 1 | 9 | 1 | ... |
Ta có: 2018 : 4 = 504 (dư 2)
Suy ra \(2017^{2018}+2019^{2018}= \overline{...9}+\overline{...1}=\overline{...0}\)
Vậy 20172018 + 20192018 chia hết cho 10
b) Làm tương tự như câu a)
Các số hạng của P là 1/n (với n là số tự nhiên). Do đó P có 99 số hạng.
Ta có:
\(P=\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{100}>\dfrac{1}{100}+\dfrac{1}{100}+...+\dfrac{1}{100}=99\cdot\dfrac{1}{100}=\dfrac{99}{100}>\dfrac{9}{10}\)
Theo đề bài, khi người thứ hai đi được 1 giờ thì người thứ nhất đi được 2 + 1 = 3 (giờ).
Khi đó người thứ nhất đi được 1/2 quãng đường, người thứ hai đi được 1/3 quãng đường.
Rõ ràng, nếu hai người đã gặp nhau thì tổng quãng đường đi được của hai người là quãng đường từ A đến B, hay là 1 phần quãng đường. Mà 1/2 + 1/3 < 1 nên hai người chưa gặp nhau.
Số chính phương có thể ở dạng (7k + n)2, với n là số nguyên có giá trị từ 0 đến 7. Xét các trường hợp sau:
- n = 0
(7k + n)2 = (7k)2, suy ra khi chia 7 dư 0.
- n ≠ 0
(7k + n)2 = 49k2 + 14nk + 2, suy ra khi chia 7 dư 2.
Tóm lại, số chính phương khi chia cho 7 thì chỉ có thể dư 0 hoặc 2, suy ra khi chia cho 7 không thể dư 3.
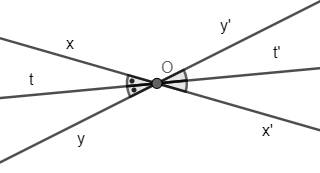
Theo đề ta có:
\(\widehat{tOx}+\widehat{t'Oy'}+\widehat{xOy'}=\dfrac{1}{2}\widehat{xOy}+\dfrac{1}{2}\widehat{x'Oy'}+\widehat{xOy'}\)
Mà \(\widehat{xOy}=\widehat{x'Oy'}\) (hai góc đối đỉnh)
Suy ra biểu thức trên bằng \(\widehat{xOy}+\widehat{xOy'}=180^o\) (hai góc kề bù)
Hay \(\widehat{tOx}+\widehat{t'Oy'}+\widehat{xOy'}=\widehat{tOt'}=180^o\)
Từ đó suy ra tt' là một góc bẹt, hay tia Ot và tia Ot' là hai tia đối nhau