

when the imposter is sus
Giới thiệu về bản thân



































b)
S = 3 + 5 - 7 - 9 + 11 + 13 - 15 - 17 + ... + 243 + 245 - 247 - 249
S = (3 - 7) + (5 - 9) + ... + (243 - 247) + (245 - 249)
S = (-4) + (-4) + ... + (-4) + (-4)
Tổng trên có số số hạng là : [(249 - 3) : 2 + 1] : 2 = 62 (số hạng)
Suy ra S = (-4) x 62 = -248
d)
E = 2 - 4 + 6 - 8 + ... + 218 - 220
E = (2 - 4) + (6 - 8) + ... + (218 - 220)
E = (-2) + (-2) + ... + (-2)
Tổng trên có số số hạng là: [(220 - 2) : 2 + 1] : 2 = 55 (số hạng)
Suy ra E = (-2) x 55 = -110
Gọi chiều dài của hình chữ nhật đó là x. Theo đề ta có:
\(\left(x\times2\right)\times x=40\)
\(x\times x\times2=40\)
\(x\times x=40\div2=20\)
Không có giá trị tự nhiên nào của x để thỏa mãn tích trên => Sai đề
Vì có đủ các bác sĩ mỗi loại cũng như điều dưỡng viên chia đều vào mỗi đội, nên để có thể thành lập được số đội phản ứng nhanh nhiều nhất có thể thì số bác sĩ mỗi loại cũng như điều dưỡng viên phải nhỏ nhất có thể. Từ đó số đội phản ứng nhanh nhiều nhất phải là ƯCLN của số bác sĩ mỗi loại cũng như điều dưỡng viên.
Ta có 18 = 2.32; 27 = 33; 45 = 32.5.
Suy ra ƯCLN(18; 27; 45) = 32 = 9.
Vậy có thể thành lập được nhiều nhất 9 đội phản ứng nhanh.
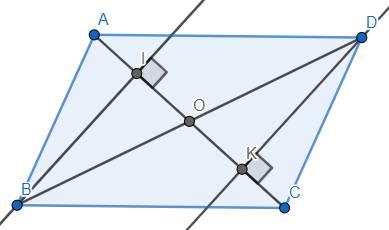
b) Vì BI vuông góc với AC tại I, nên I thuộc AC.
Vì DK vuông góc với AC tại K, nên K thuộc AC.
Vì O là giao điểm của AC và BD nên O thuộc AC.
Suy ra I, O, K là các điểm thuộc AC; từ đó ba điểm I, O, K thẳng hàng
Sửa đề: Tìm x, y thuộc Z biết x2 + 2x + y = xy
Bài làm:
\(x^2+2x+y=xy\)
\(x^2+2x=xy-y\)
\(x\left(x+2\right)=y\left(x-1\right)\)
\(\dfrac{x}{y}=\dfrac{x-1}{x+2}\)
Đặt xk = x - 1; yk = x + 2; k ≠ 0. Nếu k = 1 thì x = x - 1 hay 0 = -1, vô lí.
Suy ra
xk - x = -1
x(k - 1) = -1
\(x=-\dfrac{1}{k-1}\)
\(yk=2-\dfrac{1}{k-1}\)
\(y=\dfrac{2-\dfrac{1}{k-1}}{k}\)
(từ đoạn này thì phải tìm k để x và y nguyên nhưng chưa xử lí được)
1)
xy + x - 4y = 12
x + y(x - 4) = 12
y(x - 4) = 12 - x
\(y=\dfrac{-x+12}{x-4}\)
Vì \(x,y\inℕ\) nên
\(\left(-x+12\right)⋮\left(x-4\right)\)
\(\left(-x+12\right)-\left(x-4\right)⋮\left(x-4\right)\)
\(16⋮\left(x-4\right)\)
\(\left(x-4\right)\inƯ\left(16\right)\)
\(\left(x-4\right)\in\left\{1;-1;2;-2;4;-4;8;-8;16;-16\right\}\)
\(x\in\left\{5;3;6;2;8;0;12;-4;20;-12\right\}\)
\(y\in\left\{\dfrac{-5+12}{5-4};\dfrac{-3+12}{3-4};\dfrac{-6+12}{6-4};\dfrac{-2+12}{2-4};\dfrac{-8+12}{8-4};\dfrac{-0+12}{0-4};\dfrac{-12+12}{12-4};\dfrac{4+12}{-4-4};\dfrac{-20+12}{20-4};\dfrac{12+12}{-12-4}\right\}\)
\(y\in\left\{7;-9;3;-5;1;-3;0;-2;-\dfrac{1}{2};-\dfrac{7}{5}\right\}\)
\(\left(x;y\right)\in\left\{\left(5;7\right);\left(3;-9\right);\left(6;3\right);\left(2;-5\right);\left(8;1\right);\left(0;-3\right);\left(12;0\right);\left(-4;-2\right);\left(20;-\dfrac{1}{2}\right);\left(-12;-\dfrac{7}{5}\right)\right\}\)
Mà \(x,y\inℕ\) nên các giá trị cần tìm là \(\left(x;y\right)\in\left\{\left(5;7\right);\left(6;3\right);\left(8;1\right);\left(12;0\right)\right\}\)
2)
(2x + 3)(y - 2) = 15
\(\left(2x+3\right)\inƯ\left(15\right)\)
\(\left(2x+3\right)\in\left\{1;-1;3;-3;5;-5;15;-15\right\}\)
Ta lập bảng
| 2x + 3 | 1 | -1 | 3 | -3 | 5 | -5 | 15 | -15 |
| y - 2 | 15 | -15 | 5 | -5 | 3 | -3 | 1 | -1 |
| (x; y) | (-1; 17) | (-2; -13) | (0; 7) | (-3; -3) | (1; 5) | (-4; -1) | (6; 3) | (-9; 1) |
Mà \(x,y\inℕ\) nên các giá trị cần tìm là \(\left(x;y\right)\in\left\{\left(0;7\right);\left(1;5\right);\left(6;3\right)\right\}\)
\(A=\dfrac{7^{2020^{2019}}-3^{2016^{2015}}}{5}\)
Xét \(X=2020^{2019}\) và \(Y=2016^{2015}\). Khi đó \(A=\dfrac{7^X-3^Y}{5}\).
Vì cơ số của X tận cùng bằng 0 nên 0.0.0...0 luôn tận cùng bằng 0. Suy ra chữ số tận cùng của X là 0.
Ngoài ra, 20202019 sẽ có 2019 chữ số 0 ở sau cùng, suy ra hai chữ số tận cùng của X là những chữ số 0. Suy ra X chia hết cho 4.
Vì cơ số của Y tận cùng bằng 6 nên 6.6.6...6 luôn tận cùng bằng 6. Suy ra chữ số tận cùng của Y là 6.
Dễ dàng nhận thấy rằng 2016 chia hết cho 4, suy ra Y cũng chia hết cho 4 (y ϵ N*).
Do đó \(A=\dfrac{7^X-3^Y}{5}=\dfrac{7^{\overline{...0}}-3^{\overline{...6}}}{5}=\dfrac{7^{4x}-3^{4y}}{5}\)
Ta lập bảng
| n | 1 | 2 | 3 | 4 | ... |
| Chữ số tận cùng của 7n | 7 | 9 | 3 | 1 | ... |
| Chữ số tận cùng của 3n | 3 | 9 | 7 | 1 | ... |
Dãy trên sẽ lặp lại với chu kì là 4 số hạng. Khi đó chữ số tận cùng của 74n; 34n lần lượt giống chữ số tận cùng của 7n; 3n.
Suy ra \(A=\dfrac{\overline{...1}-\overline{...1}}{5}=\dfrac{\overline{...0}}{5}\).
Dễ nhận thấy rằng A chia hết cho 5A chia hết cho 10. Mà 10 = 5.2 nên 5A cũng chia hết cho 2. Lại có 5 không chia hết cho 2 nên chỉ có trường hợp A chia hết cho 2 (đpcm)
a = 2.4.6.8.10 + 40
Vì 2.4.6.8.10 chia hết cho 2; 5 và 8 và 40 chia hết cho 2; 5 và 8 nên a chia hết cho 2; 5 và 8.
Ta có a = 2.4.6.8.10 + 40 = 2.6.8.40 + 40 = 40(2.6.8 + 1)
Suy ra a chia hết cho 40
Gọi giá trị của biểu thức trên là A. Ta có:
\(A=\dfrac{5}{2}+\dfrac{5}{6}+\dfrac{5}{18}+\dfrac{5}{54}+\dfrac{5}{162}\)
\(3A=\dfrac{15}{2}+\dfrac{5}{2}+\dfrac{5}{6}+\dfrac{5}{18}+\dfrac{5}{54}\)
\(3A-A=\left(\dfrac{15}{2}+\dfrac{5}{2}+\dfrac{5}{6}+\dfrac{5}{18}+\dfrac{5}{54}\right)-\left(\dfrac{5}{2}+\dfrac{5}{6}+\dfrac{5}{18}+\dfrac{5}{54}+\dfrac{5}{162}\right)\)
\(2A=\dfrac{15}{2}-\dfrac{5}{162}\)
\(A=\left(\dfrac{15}{2}-\dfrac{5}{162}\right)\div2=\dfrac{605}{81}\div2=\dfrac{605}{162}\)
Ta có:
50! - 40! = 40!(41.42.43.44.45.46.47.48.49.50 - 1)
Mà 40! = 40.39.38.37...2.1 nên 40! chia hết cho 37
Suy ra 50! - 40! chia hết cho 37