\(3^x\cdot4=324\)
\(\Leftrightarrow3^x=\dfrac{324}{4}=81\)
\(\Leftrightarrow3^x=3^4\)
\(\Rightarrow x=4\)
Vậy \(x=4\)

\(\dfrac{3n+1}{3n-4}\) \(=\dfrac{3n-4+5}{3n-4}\) \(=1+\dfrac{5}{3n-4}\)
Để biểu thức nhận giá trị nguyên thì \(5⋮\left(3n-4\right)\)
\(\Rightarrow\left(3n-4\right)\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\)
 

Vậy \(x=1\) hoặc \(x=3\) thì biểu thức \(\dfrac{3n+1}{3n-4}\) nhận giá trị nguyên

\(A=\dfrac{3+2\left|x+2\right|}{1+\left|x+2\right|}\)
\(=\dfrac{2+2\left|x+2\right|+1}{1+\left|x+2\right|}\)
\(=\dfrac{2\left(1+\left|x+2\right|\right)+1}{1+\left|x+2\right|}\)
\(=\dfrac{2\left(1+\left|x+2\right|\right)}{1+\left|x+2\right|}+\dfrac{1}{1+\left|x+2\right|}\)
\(=2+\dfrac{1}{1+\left|x+2\right|}\)
Ta có \(\left|x+2\right|\ge0\)
\(\Leftrightarrow1+\left|x+2\right|\ge1\)
\(\Leftrightarrow\dfrac{1+\left|x+2\right|}{1+\left|x+2\right|}\ge\dfrac{1}{1+\left|x+2\right|}\)
\(\Leftrightarrow\dfrac{1}{1+\left|x+2\right|}\le1\)
\(\Leftrightarrow2+\dfrac{1}{1+\left|x+2\right|}\le1+2=3\)
\(\Rightarrow A\le3\)
Dấu \("="\) xảy ra khi \(x+2=0\) \(\Leftrightarrow x=-2\)
Vậy giá trị lớn nhất của biểu thức \(A\) là \(3\)

\(c.\) Xét \(\Delta BAC\) và \(\Delta IMC\) \(\left(\widehat{B}=\widehat{I}=90^o\right)\), ta có:
\(\widehat{C}\) là góc chung
\(\Rightarrow\Delta BAC\sim\Delta IMC\) \(\left(g-g\right)\)
\(\Rightarrow\dfrac{AB}{MI}=\dfrac{BC}{CI}\) \(\Rightarrow BC\cdot MI=AB\cdot CI\) \(\left(1\right)\)
Ta có \(\widehat{ABC}=90^o\)\(\Rightarrow2\widehat{MBC}=90^o\) 
\(\Rightarrow\widehat{MBC}=\dfrac{90^o}{2}=45^o\)
Xét \(\Delta BIM\), ta có:
\(\widehat{I}=90^o;\) \(\widehat{B}=45^o\) \(\left(gt\right)\)
\(\Rightarrow\Delta BIM\) vuông cân tại \(\widehat{I}\)
\(\Rightarrow BI=MI\)
Áp dụng định lí Pytago vào \(\Delta BIM\) vuông cân tại \(\widehat{I}\) ta có:
\(BM^2=BI^2+MI^2\) 
mà \(BI=MI\) \(\left(cmt\right)\)
\(\Rightarrow BM^2=2MI^2\)
\(\Rightarrow MI^2=\dfrac{BM^2}{2}\)
\(\Rightarrow MI=\dfrac{BM}{\sqrt{2}}\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow BC\cdot\dfrac{BM}{\sqrt{2}}=AB\cdot CI\)
\(\Rightarrow BC\cdot BM=\sqrt{2}AB\cdot CI\)  \(\left(đpcm\right)\)

\(a.\) Xét \(\Delta BAC\) và \(\Delta HAB\) \(\left(\widehat{B}=\widehat{H}=90^o\right)\), ta có:
\(\widehat{A}\) là góc chung
\(\Rightarrow\Delta BAC\sim\Delta HAB\) \(\left(g-g\right)\)
\(b.\) Xét \(\Delta ABC\) vuông tại \(\widehat{B}\), ta có:
\(AC^2=AB^2+BC^2\) \(\left(Pytago\right)\)
\(\Rightarrow BC^2=AC^2-AB^2=25^2-15^2=625-225=400\)
\(\Rightarrow BC=\sqrt{400}=20\) \(\left(cm\right)\)
Do \(BM\) là đường phân giác của \(\Delta ABC\)
\(\Rightarrow\dfrac{AB}{AM}=\dfrac{BC}{MC}\) \(\Rightarrow\dfrac{AB}{AC-MC}=\dfrac{BC}{MC}\)
\(\Rightarrow AB\cdot MC=BC\cdot\left(AC-MC\right)\)
\(\Leftrightarrow AB\cdot MC=AC\cdot BC-BC\cdot MC\)
\(\Leftrightarrow AB\cdot MC+BC\cdot MC=AC\cdot BC\)
\(\Leftrightarrow MC\left(AB+BC\right)=AC\cdot BC\)
\(\Leftrightarrow MC=\dfrac{AC\cdot BC}{AB+BC}=\dfrac{25\cdot20}{15+20}=\dfrac{500}{35}=\dfrac{100}{7}\approx14,29\) \(\left(cm\right)\)

Quên

\(3\dfrac{2}{5}=\dfrac{3\cdot5+2}{5}=\dfrac{17}{5}\)
\(2\dfrac{4}{9}=\dfrac{2\cdot9+4}{9}=\dfrac{22}{9}\)
\(7\dfrac{3}{8}=\dfrac{7\cdot8+3}{8}=\dfrac{59}{8}\)
\(15\dfrac{1}{10}=\dfrac{15\cdot10+1}{10}=\dfrac{151}{10}\)

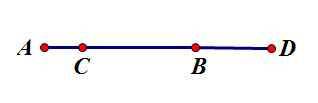
\(a.\) \(CB=AB-AC=4-1=3\) \(cm\)
\(b.\) \(CD=CB+BD=3+2=5\) \(cm\)

\(a.\) Chu vi lối đi đó là: \(2\left(12+2\right)=28\) \(\left(m\right)\)
Diện tích lối đi đó là: \(12\cdot2=24\) \(\left(m^2\right)\)
\(b.\) \(40\) \(cm\) \(=0,4\) \(m\)
Số viên gạch người ta phải lát là: \(24:0,4=60\) (viên gạch)

\(E=\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)\)
Đặt \(t=x^2+5x+5\) ta được
\(E=\left(t-1\right)\left(t+1\right)\)
\(=t^2-1\)
=\(\left(x^2+5x+5\right)^2-1\)
Dấu \("="\) xảy ra khi \(x^2+5x+5=0\)
\(\Leftrightarrow\left(x-\dfrac{-5+\sqrt{5}}{2}\right)\left(x-\dfrac{-5-\sqrt{5}}{2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{-5+\sqrt{5}}{2}=0\\x-\dfrac{-5-\sqrt{5}}{2}=0\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{-5\pm\sqrt{5}}{2}\)
Vậy giá trị nhỏ nhất của \(E\) là \(-1\)