Định lí Thalès trong tam giác SVIP

1. ĐOẠN THẲNG TỈ LỆ

a. Tỉ số của hai đoạn thẳng:

Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.

b. Nhận xét: Khi ta thay đổi đơn vị đo, tỉ số độ dài của hai đoạn thẳng AB và CD không thay đổi. 

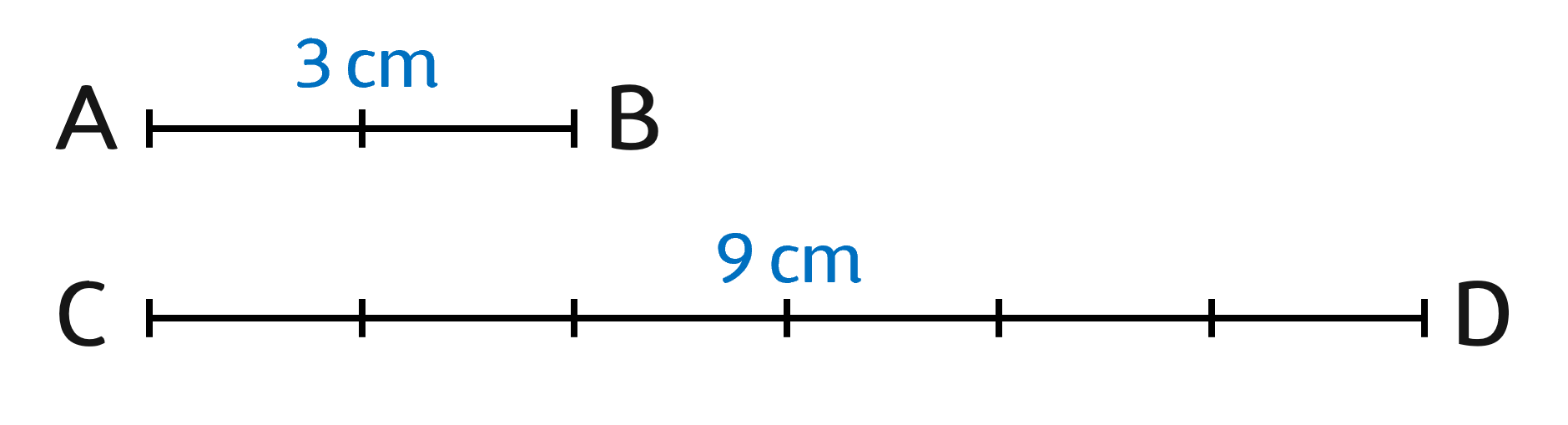
Tỉ số đó là tỉ số của hai đoạn thẳng AB và CD.

c. Đoạn thẳng tỉ lệ

Hai đoạn thẳng $AB$ và $CD$ gọi là tỉ lệ với hai đoạn thẳng $A’B’$ và $C’D’$ nếu có tỉ lệ thức:

$\dfrac{AB}{CD} = \dfrac{A'B'}{C'D'}$.

Ví dụ 1. Đoạn thẳng $AB$ gấp $5$ lần đoạn thẳng $CD$, đoạn thẳng $A'B'$ gấp $7$ lần đoạn thẳng $CD$.

a) Tỉ số của hai đoạn thẳng $AB$ và $A'B'$ là: $\dfrac{AB}{A'B'} = \dfrac{5CD}{7CD} = \dfrac{5}{7}$.

b) Cho biết đoạn thẳng $MN = 55$ cm và $M'N' = 77$ cm; hai đoạn thẳng $AB$ và $A'B'$ có tỉ lệ với đoạn thẳng $MN$ và $M'N'$ không?

 $\dfrac{MN}{M'N'} = \dfrac{55}{77} = \dfrac{5}{7} = \dfrac{AB}{A'B'} = \dfrac{MN}{M'N'}$.

Vậy hai đoạn thẳng $AB$ và $A'B'$ tỉ lệ với đoạn thẳng $MN$ và $M'N'$.

2. ĐỊNH LÍ THALÈS TRONG TAM GIÁC

ĐỊNH LÍ THALÈS

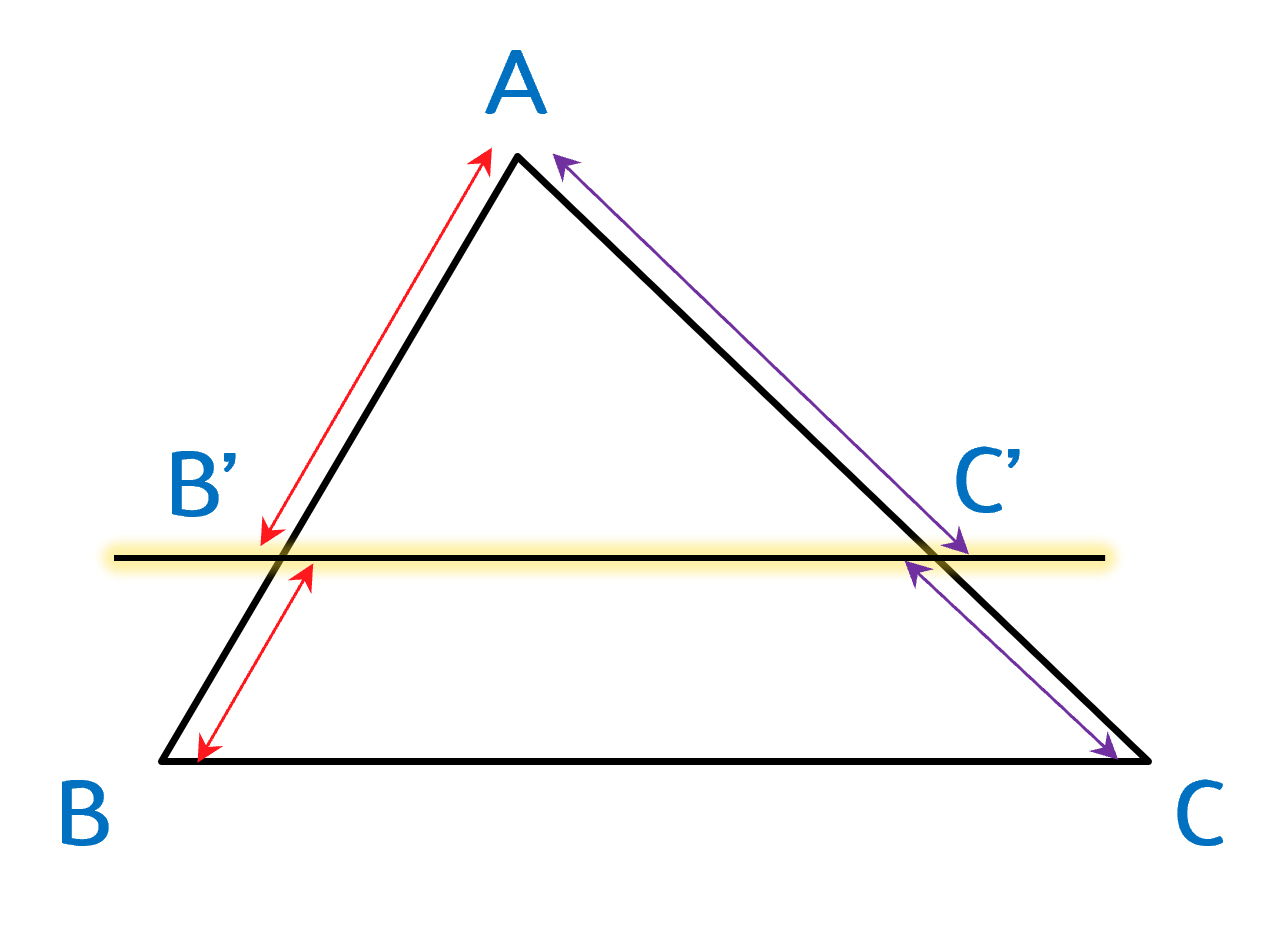
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.

Trong hình vẽ, nếu $B'C'$ // $BC$ thì

$\dfrac{AB'}{AB}=\dfrac{AC'}{AC}$; $\dfrac{AB'}{B'B}=\dfrac{AC'}{C'C}$; $\dfrac{B'B}{AB'}=\dfrac{C'C}{AC'}$.

Ví dụ 2. Cho hình vẽ dưới đây $BC$ / / $ED$. Tính độ dài đoạn $EC$

Vì $BC$ / / $ED$ nên $\dfrac{AD}{BD}=\dfrac{AE}{EC}$ (định lí Thalès)

Hay $\dfrac{2}{EC}=\dfrac{3}{4,13}$

Suy ra $ EC=2,75$.

⚡ĐỊNH LÍ THALÈS ĐẢO

Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

Trong hình vẽ, nếu có một trong hai tỉ lệ thức :

$\dfrac{AM}{AB}=\dfrac{AN}{AC};\,\dfrac{MB}{AB}=\dfrac{NC}{AC}$ thì ta có $MN$ // $BC$.

Ví dụ 3. Quan sát hình và chứng minh rằng $MN$ // $BC$.

Trong tam giác $ABC$ có: $\dfrac{AM}{MB} = \dfrac23$

$\dfrac{AN}{NC} = \dfrac46 = \dfrac23$

Vì $\dfrac{AM}{MB} = \dfrac{AN}{NC} = \dfrac23$ nên $MN$ // $BC$ (theo định lí Thalès đảo)

⚡HỆ QUẢ CỦA ĐỊNH LÍ THALÈS ĐẢO

Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.

Cho tam giác $ABC$, đường thẳng $d$ song song với cạnh $BC$ lần lượt cắt các cạnh $AB$, $AC$ tại $M$ và $N$. Khi đó, ta có :

$\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{MN}{BC}$.

Ví dụ 4. Tính $x$ trong hình dưới đây.

Xét tam giác $ABC$ có $MN$ // $BC$ nên theo hệ quả của định lí Thalès đảo, ta có:

$\dfrac{MN}{BC}=\dfrac{AM}{AB}=\dfrac{2}{3+2}$

Suy ra $MN=\dfrac{2}{5} B C=\dfrac{2}{5} . 6,5=2,6$.