Định lí Pythagore và ứng dụng SVIP

1. Định lí Pythagore

Định lí

Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

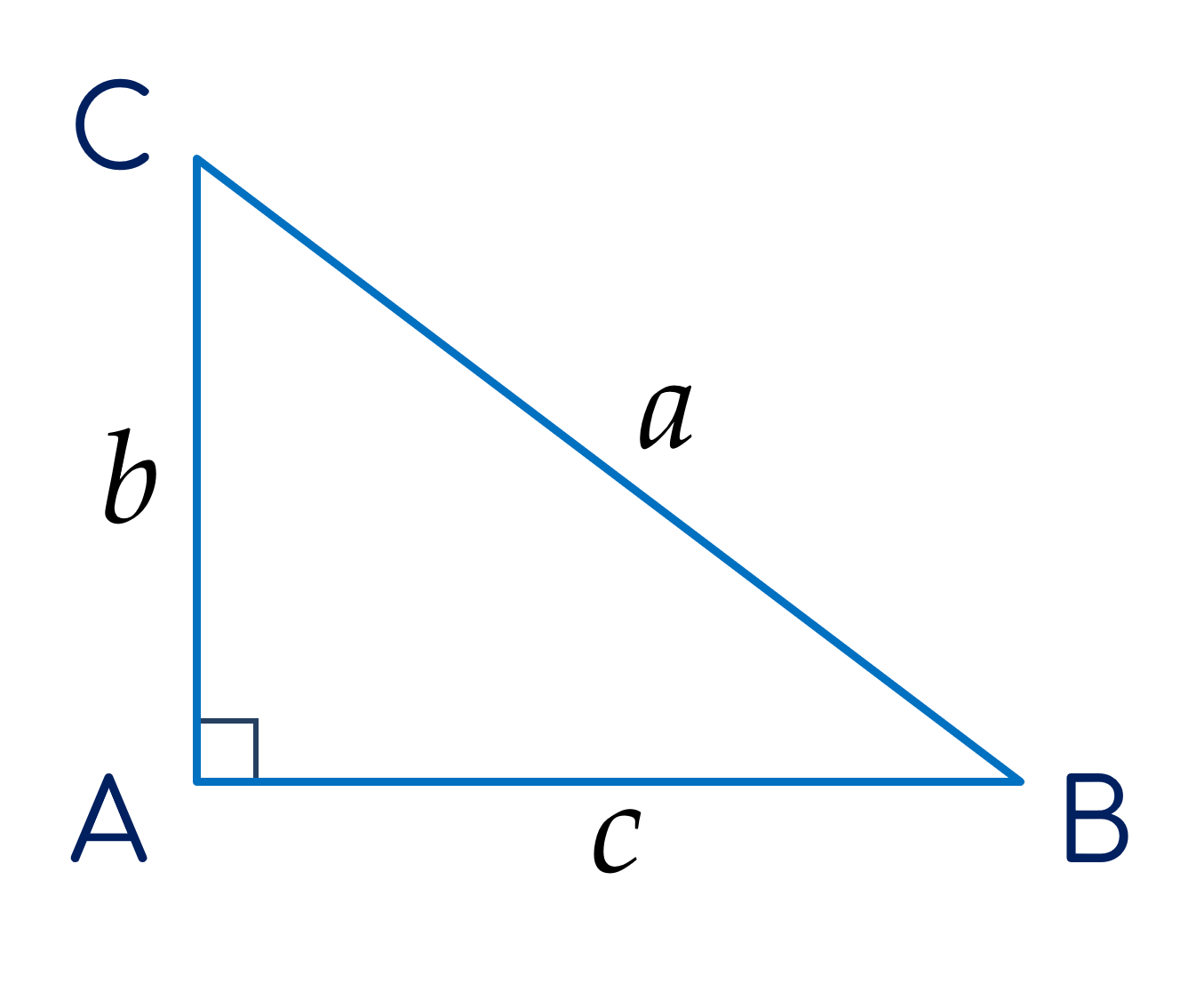
Trong tam giác ABC vuông tại A, ta có:

AB² + AC² = BC² hay a² = b² + c² (định lí Pythagore)

Ví dụ 1. 

Cho tam giác ABC vuông tại A có AB = 5 cm, AC = 12 cm. Tính độ dài BC.

Lời giải

Do $\Delta$ABC vuông tại A nên theo định lí Pythagore ta có: BC² = AB² + AC²

Suy ra BC² = 5² + 12² = 169 nên BC = 13 (cm).

Ví dụ 2. 

Cho tam giác vuông MNP có cạnh huyền NP = 10 dm và cạnh MN = 8 dm. Tính độ dài cạnh MP.

Lời giải

Áp dụng định lí Pythagore vào $\Delta$MNP có cạnh huyền NP ta có: NP² = MN² + MP²

Suy ra MP² = NP²  – MN² = 10² – 8² = 36 = 6²

Vậy MP = 6 dm.

2. Định lí Pythagore đảo

Định lí

Nếu tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.

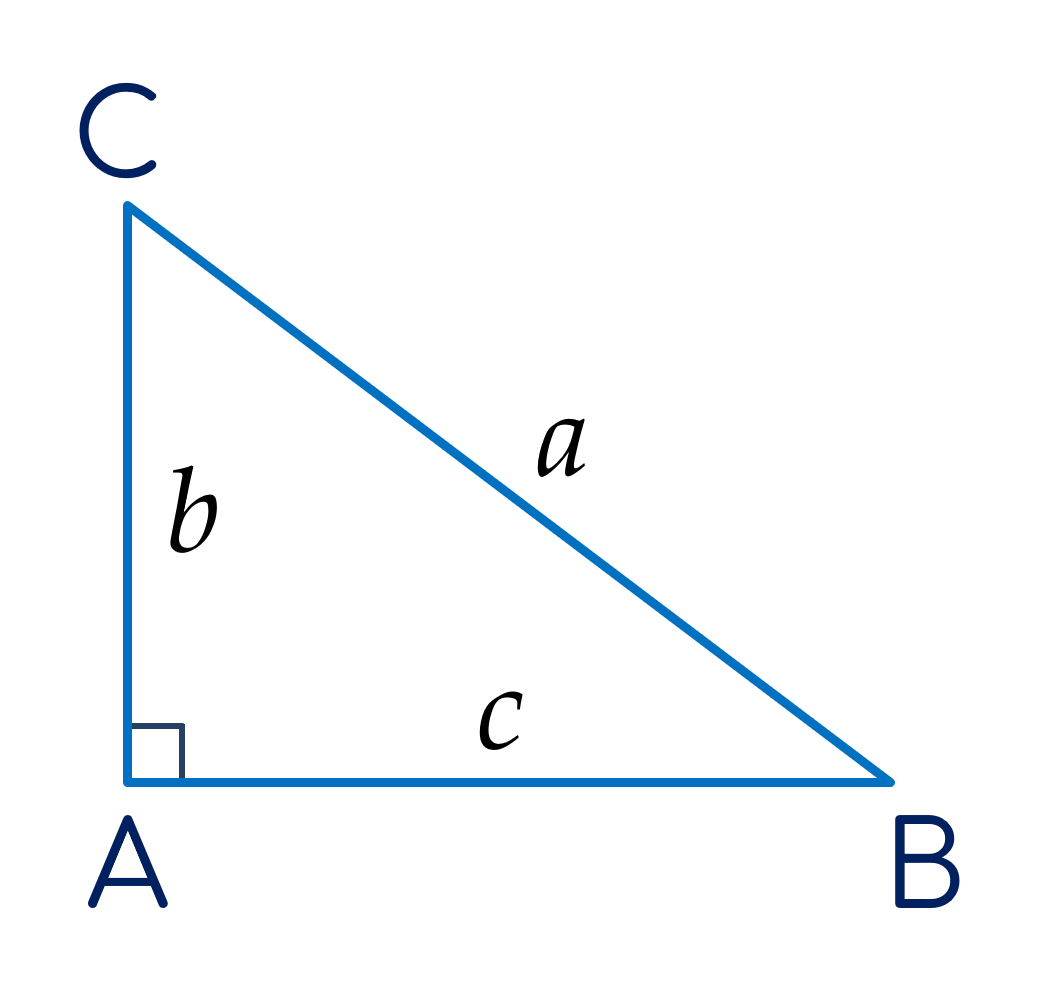
Với $\Delta$ABC, nếu BC² = AB² + AC² hay a² = b² + c² thì tam giác ABC vuông tại A.

Ví dụ 3.

Tam giác nào dưới đây là tam giác vuông?

a) Tam giác ABC có AB = 20 cm, BC = 12 cm, AC = 16 cm.

Lời giải

Ta có 20² = 12² + 16², suy ra AB² = BC² + AC².

Theo định lí Pythagore đảo ta có $\Delta$ABC vuông tại C.

b) Tam giác MNP có MN = 6 dm, NP = 11 dm, MP = 9 dm.

Lời giải

NP là cạnh dài nhất, 11² $\ne$ 6² + 9² hay NP² $\ne$ MN² + MP² nên tam giác MNP không phải tam giác vuông.

3. Ứng dụng

Ta có thể vận dụng định lí Pythagore để tính nhiều yếu tố trong khoa học và đời sống như tính độ dài đoạn thẳng, khoảng cách giữa hai điểm, chiều dài, chiều cao của vật, ...

Ví dụ 4. Một bạn học sinh thả diều ngoài đồng, cho biết đoạn dây diều từ tay bạn đến diều dài $170$ m và bạn đứng cách nơi diều được thả lên theo phương thẳng đứng là $80$ m. Tính độ cao của con diều so với mặt đất, biết tay bạn học sinh cách mặt đất $2$ m.

Lời giải

Áp dụng định lí Pythagore vào $\Delta$ ABC vuông tại A, ta có:

BC² = AB² + AC²

AB = $\sqrt{170^2-80^2}=150$

Độ cao của con diều so với mặt đất $150 + 2 = 152$ m.