Đề kiểm tra cuối học kì I - lớp 12 bộ sách Kết nối tri thức

Câu 1 (1đ):

Cho hàm số $y=f(x)$ có bảng biến thiên như sau:

Cho hàm số $y=f(x)$ có bảng biến thiên như sau

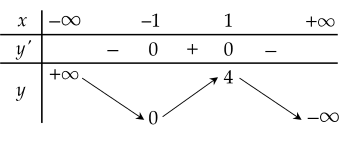
Khẳng định nào sau đây đúng?

Hàm số nghịch biến trên

(-1;+\infty)

.

Hàm số đồng biến trên

(-1;1)

.

Hàm số đồng biến trên

(-\infty ;-1)

.

Hàm số nghịch biến trên

(-1;1)

.

Câu 2 (1đ):

Hàm số $y=x^3-3x^2+4$ đồng biến trên mỗi khoảng nào sau đây?

(-\infty ;1)

và

(2;+\infty)

.

(0;2)

.

(-\infty ;0)

và

(2;+\infty)

.

(0;1)

.

Câu 3 (1đ):

Cho hàm số $y = f(x)$ có đồ thị như hình vẽ sau:

Điểm cực đại của đồ thị hàm số đã cho là

x = -1

.

N(-1;1)

.

M(-3;-3)

.

x = -3

.

Câu 4 (1đ):

Đồ thị hàm số $y=\dfrac{3x-1}{2x+1}$ có tâm đối xứng là

\Big(\dfrac{1}{2};\dfrac{3}{2}\Big)

.

\Big(-\dfrac{1}{2};-\dfrac{3}{2}\Big)

.

\Big(\dfrac{1}{2};-\dfrac{3}{2}\Big)

.

\Big(-\dfrac{1}{2};\dfrac{3}{2} \Big)

.

Câu 5 (1đ):

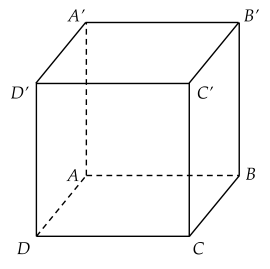
Cho hình lập phương $ABCD.{A}'{B}'{C}'{D}'$ . Vectơ nào sau đây có điểm đầu và điểm cuối là đỉnh của hình lập phương $ABCD.{A}'{B}'{C}'{D}'$ và bằng $\overrightarrow{AD}$ ?

loading...

\overrightarrow{CB}

.

\overrightarrow{{B}'{C}'}

.

\overrightarrow{AB}

.

\overrightarrow{DA}

.

Câu 6 (1đ):

Trong không gian với hệ tọa độ $Oxyz$ , cho hai điểm $A(-1;1;-2 ),\,B(1;3;0 )$ . Khi đó tọa độ $\overrightarrow{AB}$ bằng

\overrightarrow{AB}=(0;4;-2 )

.

\overrightarrow{AB}=(0;2;-1 )

.

\overrightarrow{AB}=(2;2;2 )

.

\overrightarrow{AB}=(-2;-2;-2 )

.

Câu 7 (1đ):

Cho mẫu số liệu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên của một công ty như sau:

Thời gian	Số nhân viên
$[15;20)$	$6$
$[20;25)$	$14$
$[25;30)$	$25$
$[30;35)$	$37$
$[35;40)$	$21$
$[40;45)$	$13$
$[45;50)$	$9$

Khoảng biến thiên của mẫu số liệu trên là

35

.

10

.

50

.

45

.

Câu 8 (1đ):

Một ý nghĩa của khoảng tứ phân vị là

Khoảng tứ phân vị của mẫu số liệu ghép nhóm giúp xác định các giá trị không bất thường của mẫu số liệu đó.

Khoảng tứ phân vị của mẫu số liệu ghép nhóm xấp xỉ khoảng tứ phân vị của mẫu số liệu gốc và là một đại lượng cho biết mức độ không phân tán của nửa giữa mẫu số liệu.

Khoảng tứ phân vị của mẫu số liệu ghép nhóm xấp xỉ khoảng tứ phân vị của mẫu số liệu gốc và là một đại lượng cho biết mức độ phân tán của nửa giữa mẫu số liệu.

Khoảng tứ phân vị thường không được sử dụng thay cho khoảng biến thiên.

Câu 9 (1đ):

Trong không gian với hệ tọa độ $Oxyz$ , cho điểm $A(1;1;2)$ . Tọa độ điểm $A'\in (Oxy)$ sao cho độ dài đoạn thẳng $AA'$ ngắn nhất là

A'(1;1;0)

.

A'(2;-1;2)

.

A'(2;2;0)

.

A'(-1;1;0)

.

Câu 10 (1đ):

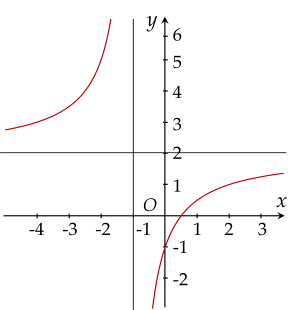
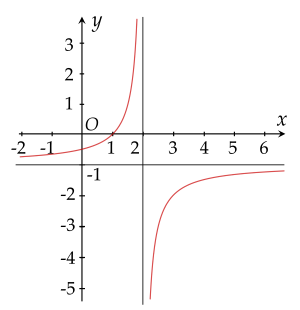
Đường cong nào sau đây là đồ thị của hàm số $y=\dfrac{1-x}{x+1}$ ?

Câu 11 (1đ):

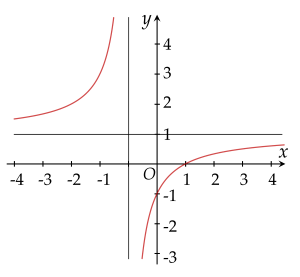
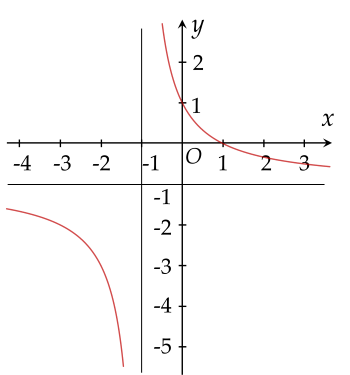
Trên đoạn $[-2;2]$ , hàm số $y=\dfrac{mx}{x^2+1}$ đạt giá trị lớn nhất tại $x=1$ khi và chỉ khi

m=-2.

m\lt 0.

m=2.

m\ge 0.

Câu 12 (1đ):

Trong không gian với hệ trục tọa độ $O x y z$ , cho tam giác $A B C$ có ba đỉnh $A(-1 ; 1 ;-3)$ , $B (4 ; 2 ; 1)$ , $C( 3 ; 0 ; 5)$ . Tọa độ trọng tâm $G$ của tam giác $A B C$ là

G (2 ; 1 ; 1).

G (3 ; 1 ; 1).

G (1 ; 3 ; 2).

G(-1 ; 2 ; 1).

Câu 13 (1đ):

Cho hàm số $y=f(x)$ liên tục và có đồ thị trên đoạn $[-2 ; 4]$ như hình vẽ.

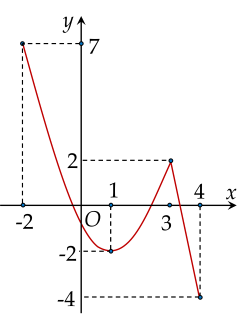
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Trên đoạn $[-2 ; 4]$ , đồ thị hàm số $y = f(x)$ có $2$ điểm cực trị.
b) Giá trị nhỏ nhất của hàm số $y = f(x)$ trên đoạn $[-2;2]$ là $-2$ .
c) Giá trị lớn nhất của hàm số $y = f(x)$ trên đoạn $[1;4]$ là $-4$ .
d) Hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = f(x)$ trên đoạn $[-2;4]$ là $11$ .

Câu 14 (1đ):

Biểu đồ dưới đây mô tả kết quả điều tra về mức lương khởi điểm (đơn vị: triệu đồng) của một số công nhân ở hai khu vực $A$ và $B$ .

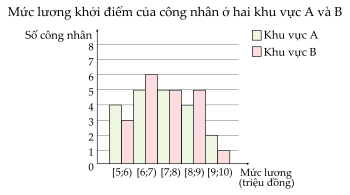
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Hai khu vực $A$ và $B$ có mức lương trung bình bằng nhau.
b) Phương sai của mẫu số liệu ở khu vực $A$ lớn hơn $1,5.$
c) Độ lệch chuẩn của mẫu số liệu ở khu vực $B$ lớn hơn $1,2$ .
d) Mức lương khởi điểm của công nhân khu vực $B$ đồng đều hơn của công nhân khu vực $A$ .

Câu 15 (1đ):

Trong không gian, cho tứ diện $ABCD$ . Trên cạnh $AD$ và $BC$ lần lượt lấy các điểm $M,N$ sao cho $AM=3MD$ và $BN=3NC$ . Gọi $P,Q$ lần lượt là trung điểm $AD$ và $BC$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\overrightarrow{PQ}=\overrightarrow{AC}+\overrightarrow{DB}$ .
b) $\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AC}+\overrightarrow{CN}$ .
c) $\overrightarrow{MN}=\overrightarrow{MD}+\overrightarrow{DB}+\overrightarrow{BN}$ .
d) $\overrightarrow{BD},\overrightarrow{AC},\overrightarrow{MN}$ không đồng phẳng.

Câu 16 (1đ):

Cho hàm số $f(x)=\dfrac{-2x+3}{x-2}$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Hàm số đồng biến trên $\mathbb{R}\backslash \left\{ 2 \right\}$ .
b) Đồ thị hàm số cắt trục tung tại điểm $M(0;\dfrac{-3}{2})$ .
c) Đồ thị hàm số $y=f(x)$ cắt đường thẳng $y=x-2m$ tại hai điểm phân biệt khi $\left[ \begin{aligned} & m>3 \\ & m\lt 1 \end{aligned} \right.$ .
d) Đồ thị hàm số $y=f(x)$ cắt đường thẳng $y=x+2$ tại hai điểm phân biệt $M$ và $N$ . Biết $I$ là trung điểm của đoạn thẳng $MN$ . Khi đó hoành độ của điểm $I$ là $1$ .

Câu 17 (1đ):

Trong bài thực hành của môn huấn luyện quân sự có tình huống chiến sĩ phải bơi qua một con sông để tấn công một mục tiêu ở phía bờ bên kia sông. Biết rằng lòng sông rộng $100$ m và vận tốc bơi của chiến sĩ bằng một nửa vận tốc chạy trên bờ. Nếu như dòng sông là thẳng, mục tiêu ở cách chiến sĩ $1$ km theo đường chim bay thì người chiến sĩ phải bơi bao nhiêu mét để đến được mục tiêu nhanh nhất? (kết quả làm tròn đến hàng đơn vị)

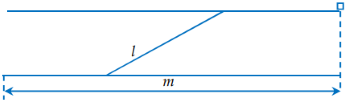
loading...

Trả lời:

Câu 18 (1đ):

Có tất cả bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y=\Big(\dfrac{1}{5}\Big)^{\frac{mx+1}{x+m}}$ đồng biến trên khoảng $\Big(\dfrac12;+\infty\Big)$ ?

Trả lời:

Câu 19 (1đ):

Với $m$ là một tham số thực thì đồ thị hàm số $y={{x}^{3}}-2{{x}^{2}}+x-1$ và đường thẳng $y=m$ có nhiều nhất bao nhiêu giao điểm?

Trả lời:

Câu 20 (1đ):

Giả sử chi phí cho xuất bản $x$ cuốn tạp chí (gồm: lương cán bộ, công nhân viên, giấy in,...) được cho bởi công thức:

$C(x)=0,0001 x^2-0,2 x+10\,000$

trong đó $C(x)$ được tính theo đơn vị là vạn đồng ( $1$ vạn đồng $=10\,000$ đồng). Chi phí phát hành cho mỗi cuốn là $4$ nghìn đồng. Tỉ số $M(x)=\dfrac{T(x)}{x}$ được gọi là chi phí trung bình cho một cuốn tạp chí khi xuất bản $x$ cuốn và tổng chỉ phí $T(x)$ (xuất bản và phát hành) cho $x$ cuốn tạp chí. Chi phí trung bình thấp nhất cho một cuốn tạp chí là bao nhiêu vạn đồng, biết rằng nhu cầu hiện tại xuất bản không quá $30\,000$ cuốn?

Trả lời:

Câu 21 (1đ):

Có ba lực cùng tác động vào một vật. Hai trong ba lực này hợp với nhau một góc $100^\circ$ và có độ lớn lần lượt là $25$ N và $12$ N. Lực thứ ba vuông góc với mặt phẳng tạo bởi hai lực đã cho và có độ lớn $4$ N. Tính độ lớn của hợp lực của ba lực trên. (làm tròn đến hàng đơn vị)

Trả lời:

Câu 22 (1đ):

Cho biểu đồ thống kê chiều cao của học sinh nữ lớp 12A:

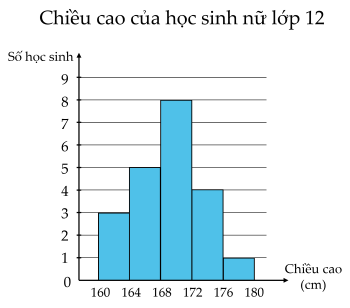
loading...

Tính độ lệch chuẩn của mẫu số liệu trên. (Làm tròn kết quả đến chữ số hàng phần trăm)

Trả lời: .

Bài học cùng chủ đề

Đề kiểm tra cuối học kì I - lớp 12 bộ sách Kết nối tri thức SVIP

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra cuối học kì I - lớp 12 bộ sách Kết nối tri thức SVIP

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP