Cho góc nhọn alpha . Tìm tan alpha nếu biết : a)sin alpha=1/3 b)cos alpha=2/căn5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 3.2
Để pt có 2 nghiệm pb thì:
$\Delta=(2m+3)^2+4(2m+4)>0$
$\Leftrightarrow (2m+3)^2+4(2m+3)+4>0$
$\Leftrightarrow (2m+3+2)^2>0\Leftrightarrow (2m+5)^2>0$
$\Leftrightarrow 2m+5\neq 0$
$\Leftrightarrow m\neq \frac{-5}{2}$
Áp dụng định lý Viet, với $x_1,x_2$ là nghiệm của pt (1) thì:
$x_1+x_2=2m+3$
$x_1x_2=-2m-4$
$\Rightarrow x_1+x_2+x_1x_2+1=0$
$\Leftrightarrow (x_1+1)(x_2+1)=0$
$\Leftrightarrow x_1=-1$ hoặc $x_2=-1$
Nếu $x_1=-1$ thì $x_2=2m+4$. Nếu $x_2=-1$ thì $x_1=2m+4$
Không mất tổng quát giả sử $x_1=-1; x_2=2m+4$
Khi đó:
$|x_1|+|x_2|=5$
$\Leftrightarrow |-1|+|2m+4|=5$
$\Leftrightarrow |2m+4|=4$
$\Leftrightarrow 2m+4=\pm 4$
$\Leftrightarrow m=0$ hoặc $m=-4$
Do $m> \frac{-5}{2}$ nên $m=0$

Lời giải:
a.
Khi $m=1$ thì PT trở thành:
$x^2-4x+4=0$
$\Leftrightarrow (x-2)^2=0\Leftrightarrow x-2=0\Leftrightarrow x=2$
b.
Để PT có 2 nghiệm pb $x_1,x_2$ thì:
$\Delta'=(m+1)^2-(m^2-2m+5)>0$
$\Leftrightarrow m>1$
Áp dụng định lý Viet:
$x_1+x_2=2(m+1)$
$x_1x_2=m^2-2m+5$
Với $m>1$ thì $x_1+x_2=2(m+1)>0; x_1x_2=m^2-2m+5>0$
$\Rightarrow x_1>0; x_2>0$
Khi đó:
$\sqrt{4x_1^2+4mx_1+m^2}+\sqrt{x_2^2+4mx_2+4m^2}=7m+2$
$\Leftrightarrow \sqrt{(2x_1+m)^2}+\sqrt{(x_2+2m)^2}=7m+2$
$\Leftrightarrow |2x_1+m|+|x_2+2m|=7m+2$
$\Leftrightarrow 2x_1+m+x_2+2m=7m+2$
$\Leftrightarrow x_1+(x_1+x_2)=4m+2$
$\Leftrightarrow x_1+2m+2=4m+2$
$\Leftrightarrow x_1=2m$
$x_2=2(m+1)-x_1=2$
$m^2-2m+5=x_1x_2=2m.2=4m$
$\Leftrightarrow m^2-6m+5=0$
$\Leftrightarrow (m-1)(m-5)=0$
Do $m>1$ nên $m=5$
Lời giải:
a.
Khi 𝑚=1m=1 thì PT trở thành:
𝑥2−4𝑥+4=0x2−4x+4=0
⇔(𝑥−2)2=0⇔𝑥−2=0⇔𝑥=2⇔(x−2)2=0⇔x−2=0⇔x=2
b.
Để PT có 2 nghiệm pb 𝑥1,𝑥2x1,x2 thì:
Δ′=(𝑚+1)2−(𝑚2−2𝑚+5)>0Δ′=(m+1)2−(m2−2m+5)>0
⇔𝑚>1⇔m>1
Áp dụng định lý Viet:
𝑥1+𝑥2=2(𝑚+1)x1+x2=2(m+1)
𝑥1𝑥2=𝑚2−2𝑚+5x1x2=m2−2m+5
Với 𝑚>1m>1 thì 𝑥1+𝑥2=2(𝑚+1)>0;𝑥1𝑥2=𝑚2−2𝑚+5>0x1+x2=2(m+1)>0;x1x2=m2−2m+5>0
⇒𝑥1>0;𝑥2>0⇒x1>0;x2>0
Khi đó:
4𝑥12+4𝑚𝑥1+𝑚2+𝑥22+4𝑚𝑥2+4𝑚2=7𝑚+24x12+4mx1+m2+x22+4mx2+4m2=7m+2
⇔(2𝑥1+𝑚)2+(𝑥2+2𝑚)2=7𝑚+2⇔(2x1+m)2+(x2+2m)2=7m+2
⇔∣2𝑥1+𝑚∣+∣𝑥2+2𝑚∣=7𝑚+2⇔∣2x1+m∣+∣x2+2m∣=7m+2
⇔2𝑥1+𝑚+𝑥2+2𝑚=7𝑚+2⇔2x1+m+x2+2m=7m+2
⇔𝑥1+(𝑥1+𝑥2)=4𝑚+2⇔x1+(x1+x2)=4m+2
⇔𝑥1+2𝑚+2=4𝑚+2⇔x1+2m+2=4m+2
⇔𝑥1=2𝑚⇔x1=2m
𝑥2=2(𝑚+1)−𝑥1=2x2=2(m+1)−x1=2
𝑚2−2𝑚+5=𝑥1𝑥2=2𝑚.2=4𝑚m2−2m+5=x1x2=2m.2=4m
⇔𝑚2−6𝑚+5=0⇔m2−6m+5=0
⇔(𝑚−1)(𝑚−5)=0⇔(m−1)(m−5)=0
Do 𝑚>1m>1 nên 𝑚=5m=5

Câu 3:
Ta thấy $\Delta'=(m^2+2)^2+2m^2+5>0$ với mọi $m\in\mathbb{R}$ nên PT luôn có 2 nghiệm pb với mọi $m$
Áp dụng định lý Viet:
$x_1+x_2=-2(m^2+2)$
$x_1x_2=-2m^2-5$
$\Rightarrow x_1x_2+1=x_1+x_2$
$\Leftrightarrow (x_1-1)(x_2-1)=0$
$\Leftrightarrow x_1=1$ hoặc $x_2=1$
Nếu $x_2=1$ thì $x_1=(-2m^2-5):x_2=-2m^2-5$
Mà $x_1>x_2$ nên $-2m^2-5>1$ (vô lý)
Do đó $x_1=1$. Khi đó $x_2=-2m^2-5$
Ta có:
$x_1x_2+8x_1^3+5=0$
$\Leftrightarrow -2m^2-5+8+5=0$
$\Leftrightarrow 8=2m^2$
$\Leftrightarrow m^2=4\Leftrightarrow m=\pm 2$


ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\x\ne9\end{matrix}\right.\)
\(B=\left(\dfrac{3}{x+3\sqrt{x}}-\dfrac{1}{\sqrt{x}-3}\right)\cdot\dfrac{x-9}{\sqrt{x}}\)
\(=\left(\dfrac{3}{\sqrt{x}\cdot\left(\sqrt{x}+3\right)}-\dfrac{1}{\sqrt{x}-3}\right)\cdot\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\sqrt{x}}\)
\(=\dfrac{3\left(\sqrt{x}-3\right)-x-3\sqrt{x}}{\left(\sqrt{x}-3\right)\cdot\left(\sqrt{x}+3\right)\cdot\sqrt{x}}\cdot\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\sqrt{x}}\)
\(=\dfrac{3\sqrt{x}-9-x-3\sqrt{x}}{x}=\dfrac{-x-9}{x}\)

Gọi số dãy ghế ban đầu trong hội trường là x(dãy)
(Điều kiện: \(x\in Z^+\))
Số ghế ban đầu trong 1 dãy ghế là \(\dfrac{120}{x}\left(ghế\right)\)
Số ghế lúc sau trong 1 dãy ghế là \(\dfrac{120}{x-2}\left(ghế\right)\)
Theo đề, ta có phương trình:
\(\dfrac{120}{x-2}-\dfrac{120}{x}=2\)
=>\(\dfrac{120x-120\left(x-2\right)}{x\left(x-2\right)}=2\)
=>\(2x\left(x-2\right)=120x-120x+240=240\)
=>x(x-2)=120
=>\(x^2-2x-120=0\)
=>(x-12)(x+10)=0
=>\(\left[{}\begin{matrix}x=12\left(nhận\right)\\x=-10\left(loại\right)\end{matrix}\right.\)
vậy: lúc đầu trong hội trường có 12 dãy ghế, mỗi dãy ghế có 120:12=10 ghế

a: Phương trình hoành độ giao điểm là:
\(x^2=2\left(m-2\right)x-m^2+4m+5\)
=>\(x^2-\left(2m-4\right)x+m^2-4m-5=0\)(1)
\(\Delta=\left[-\left(2m-4\right)\right]^2-4\cdot1\cdot\left(m^2-4m-5\right)\)
\(=4m^2-16m+16-4m^2+16m+20=36\)>0
=>(P) luôn cắt (d) tại hai điểm phân biệt
b: Vì \(\Delta=36\)
nên phương trình (1) luôn có 2 nghiệm phân biệt là:
\(\left[{}\begin{matrix}x=\dfrac{2m-4+\sqrt{36}}{2}=\dfrac{2m-4+6}{2}=\dfrac{2m+2}{2}=m+1\\x=\dfrac{2m-4-6}{2}=\dfrac{2m-10}{2}=m-5\end{matrix}\right.\)
\(\sqrt{x_1}=x_2+6\)
=>\(\left[{}\begin{matrix}\sqrt{m+1}=m-5+6\\\sqrt{m-5}=m+1+6\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\sqrt{m+1}=m+1\\\sqrt{m-5}=m+7\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\left\{{}\begin{matrix}m>=-1\\\left(m+1\right)^2=\left(m+1\right)\end{matrix}\right.\\\left\{{}\begin{matrix}m>=5\\\left(m+7\right)^2=m-5\end{matrix}\right.\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\left\{{}\begin{matrix}m>=-1\\m\left(m+1\right)=0\end{matrix}\right.\\\left\{{}\begin{matrix}m>=5\\m^2+14m+49-m+5=0\end{matrix}\right.\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}m\in\left\{0;-1\right\}\\\left\{{}\begin{matrix}m>=5\\m^2+13m+54=0\end{matrix}\right.\end{matrix}\right.\)
=>\(m\in\left\{0;-1\right\}\)
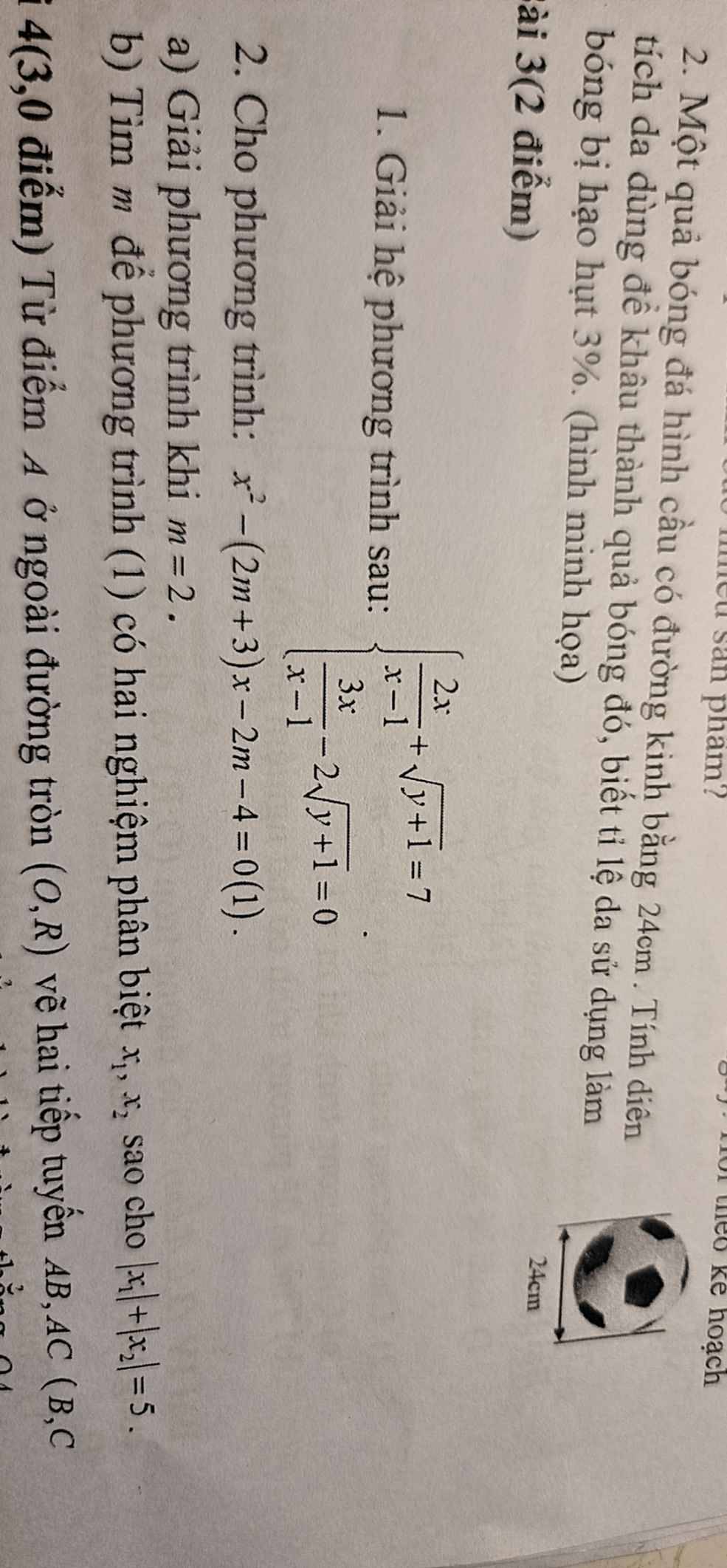
 ai chỉ em với cần gấp lắm cảm ơn
ai chỉ em với cần gấp lắm cảm ơn






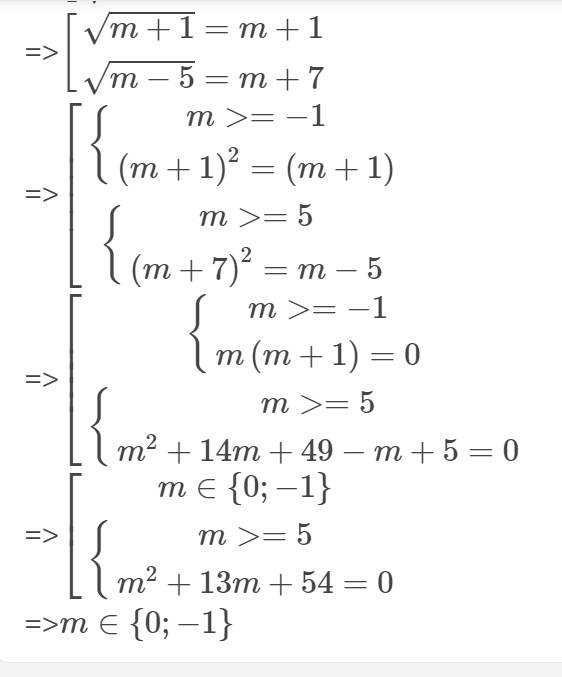
a: \(1+cot^2\alpha=\dfrac{1}{sin^2\alpha}\)
=>\(cot^2\alpha=1:\dfrac{1}{9}-1=9-1=8\)
=>\(cot\alpha=2\sqrt{2}\)
=>\(tan\alpha=\dfrac{1}{2\sqrt{2}}=\dfrac{\sqrt{2}}{4}\)
b: \(1+tan^2\alpha=\dfrac{1}{cos^2\alpha}\)
=>\(1+tan^2\alpha=1:\left(\dfrac{2}{\sqrt{5}}\right)^2=\dfrac{5}{4}\)
=>\(tan^2\alpha=\dfrac{1}{4}\)
=>\(tan\alpha=\dfrac{1}{2}\)