\(2\left(x-\dfrac{1}{3}\right)-3\left(x-1\right)=\dfrac{2}{3}\left(2-3x\right)\)

=> \(2x-\dfrac{2}{3}-3x+3=\dfrac{4}{3}-2x\)

=> \(2x-\dfrac{2}{3}-3x+3-\dfrac{4}{3}+2x=0\)

=> \(2x-3x+2x-\dfrac{2}{3}+3-\dfrac{4}{3}=0\)

=> \(x+3-\left(\dfrac{2}{3}+\dfrac{4}{3}\right)=0\)

=> \(x+3-\dfrac{6}{3}=0\)

=> \(x+3-2=0\)

=> \(x+1=0\)

=> ` x = 0 - 1`

=> `x = -1`

bằng -1 nha

\(\dfrac{3}{1^2.2^2}+\dfrac{5}{2^2.3^2}+...+\dfrac{19}{9^2.10^2}\)

= \(\dfrac{3}{1.4.}+\dfrac{5}{4.9}+...+\dfrac{19}{81.100}\)

= \(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{9}+...+\dfrac{1}{81}+\dfrac{1}{100}\)

= \(1-\dfrac{1}{100}< 1\) (đpcm)

--------------------------------

Cho các số: a;b;c thuộc `N`; `c,b` khác `0` ta luôn có:

Nếu: `c-b = a` thì: 

\(\dfrac{a}{b.c}=\dfrac{1}{b}-\dfrac{1}{c}\)

`a` là số tự nhiên không chia hết cho `3` nên a có dạng: 

`a = 3k + 1` hoặc `a = 3k + 2`

(`k` thuộc `N`*)

Mà a là số tự nhiên lẻ `=> a^2` là số tự nhiên lẻ `=> a^2 - 1` là số chẵn 

`=> a^2 ⋮ 2`

Để `a^2 - 1 ⋮ 6` thì  `a^2 - 1 ⋮ 3` (Vì `UCLN(2;3) = 1`)

- Xét `a = 3k + 1`

`=> a^2 -1 = (3k+1)^2 -1= 9k^2 + 6k + 1 - 1= 9k^2 + 6k^2 ⋮ 3` (Thỏa mãn)

- Xét `a = 3k + 2`

`=> a^2 -1 = (3k+2)^2 -1 = 9k^2 + 12k + 4 - 1= 9k^2 + 12k^2 + 3 ⋮ 3` (Thỏa mãn)

Vậy ...

\(\left(x+5\right)^2-4x^2\\=\left(x+5\right)^2-\left(2x\right)^2\\ =\left[\left(x+5\right)-2x\right]\left[\left(x+5\right)+2x\right]\\ =\left(x+5-2x\right)\left(x+5+2x\right)\\ =\left(-x+5\right)\left(3x+5\right)\)

\(x^2-9x-26=0\)

\(\text{Δ}=\left(-9\right)^2-4\cdot1\cdot\left(-26\right)=81+104=185>0\)

Do đó: Phương trình có hai nghiệm phân biệt là:

\(\left[{}\begin{matrix}x=\dfrac{9-\sqrt{185}}{2}\\x=\dfrac{9+\sqrt{185}}{2}\end{matrix}\right.\)

TY :>

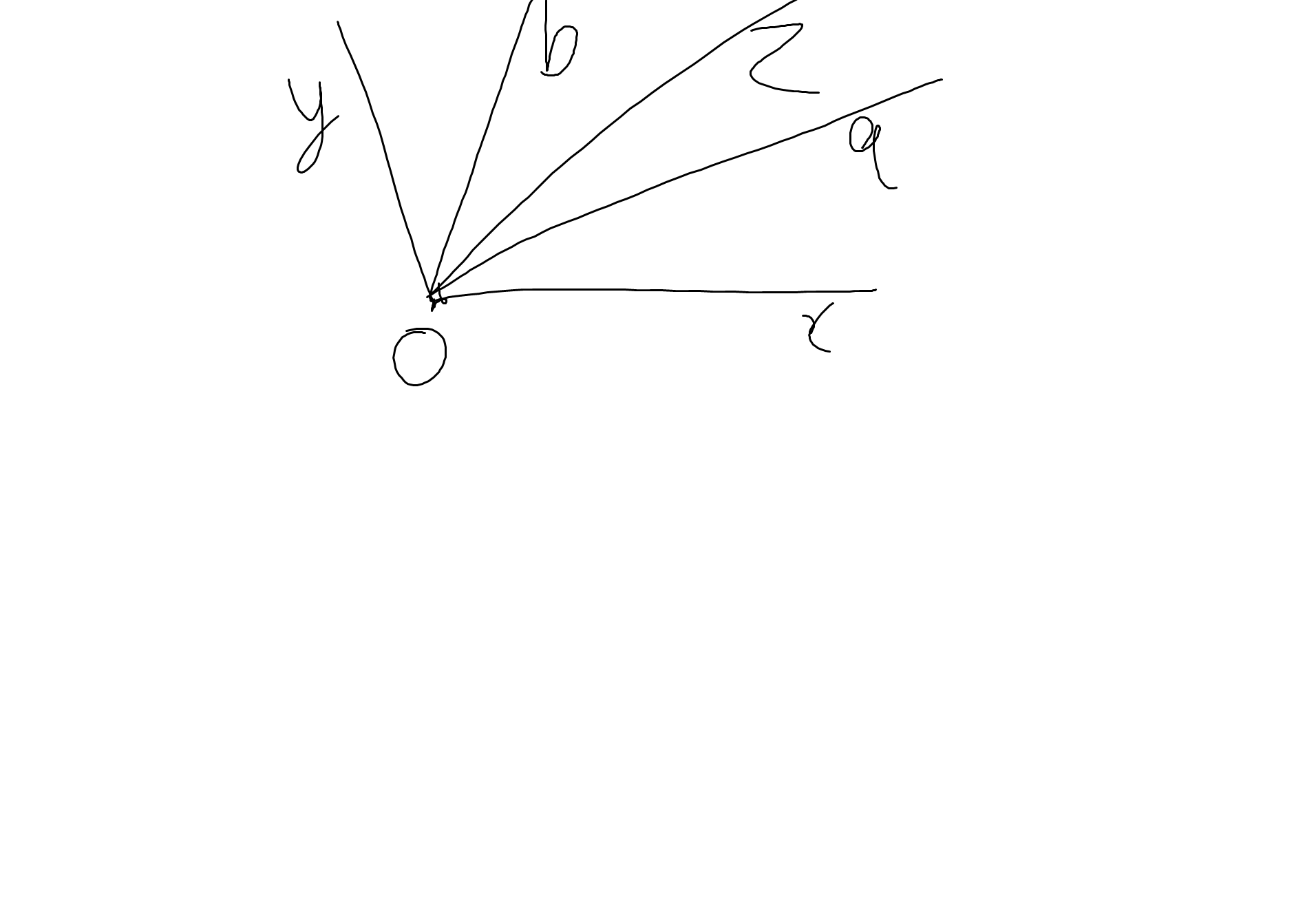
Oa là phân giác của góc xOz

=>\(\widehat{zOa}=\dfrac{\widehat{xOz}}{2}\)

Ob là phân giác của góc zOy

=>\(\widehat{zOb}=\dfrac{\widehat{zOy}}{2}\)

\(\widehat{aOb}=\widehat{zOa}+\widehat{zOb}=\dfrac{1}{2}\left(\widehat{xOz}+\widehat{zOy}\right)\)

\(=\dfrac{1}{2}\cdot\widehat{xOy}=\dfrac{1}{2}\cdot150^0=75^0\)

`(a_1 + a_2+... + a_9)/(a_3+a_6+a_9)`

`= ((a_3+a_6+a_9) + (a_2+a_5+a_8) + (a_1+a_4+a_7))/(a_3+a_6+a_9)`

`<= (3.(a_3+a_6+a_9))/(a_3+a_6+a_9) = 3 < 5`.

a: Xét ΔBAD vuông tại A và ΔBMD vuông tại M có

BD chung

\(\widehat{ABD}=\widehat{MBD}\)

Do đó: ΔBAD=ΔBMD

b: ΔBAD=ΔBMD

=>DA=DM

mà DM<DC(ΔDMC vuông tại M)

nên DA<DC

c: XétΔBKC có

KM,CA là các đường cao

KM cắt CA tại D

Do đó: D là trực tâm của ΔBKC

=>BD\(\perp\)KC tại N

Xét ΔDAK vuông tại A và ΔDMC vuông tại M có

DA=DM

\(\widehat{ADK}=\widehat{MDC}\)(hai góc đối đỉnh)

Do đó: ΔDAK=ΔDMC

=>DK=DC

=>ΔDKC cân tại D

Vòi 1 trong 1 giờ chảy được số phần bể là: 

`1 : 8 =` \(\dfrac{1}{8}\) (bể)

Vòi 2 trong 1 giờ chảy được số phần bể là: 

`1 : 6 =` \(\dfrac{1}{6}\) (bể)

Vòi 3 trong 1 giờ tháo được số phần bể là: 

`1 : 4 =` \(\dfrac{1}{4}\) (bể)

Cả 3 vòi cùng hoạt động thì trong 1 giờ chảy được số phần bể là: 

\(\dfrac{1}{8}+\dfrac{1}{6}-\dfrac{1}{4}=\dfrac{1}{24}\) (bể) 

Đáp số: ...