Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tổng 2 số đó là:
404 x 2 = 808
Nếu viết thêm chữ số 7 vào bên trái số thứ nhất \(\rightarrow\) số đó tăng thêm 700 đơn vị \(\rightarrow\) số thứ nhất bé hơn số thứ hai 700 đơn vị
Số thứ nhất là: ( 808 - 700 ) : 2 = 54
Số thứ hai là: 700 + 54 = 754
Đáp số: Số thứ nhất: 54
Số thứ hai: 754

Bài 10:
Đặt \(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=k\)
=>\(\left\{{}\begin{matrix}c=dk\\b=ck=dk\cdot k=dk^2\\a=bk=dk^2\cdot k=dk^3\end{matrix}\right.\)
a:
\(\left(\dfrac{a+b+c}{b+c+d}\right)^3=\left(\dfrac{dk^3+dk^2+dk}{dk^2+dk+d}\right)^3=\left(\dfrac{dk\left(k^2+k+1\right)}{d\left(k^2+k+1\right)}\right)^3=k^3\)
\(\dfrac{a}{d}=\dfrac{dk^3}{d}=k^3\)
Do đó: \(\dfrac{a}{d}=\left(\dfrac{a+b+c}{b+c+d}\right)^3\)
b: Sửa đề: Chứng minh \(\dfrac{a^3+c^3+b^3}{c^3+b^3+d^3}=\dfrac{a}{d}\)
\(\dfrac{a^3+c^3+b^3}{c^3+b^3+d^3}=\dfrac{\left(dk^3\right)^3+\left(dk\right)^3+\left(dk^2\right)^3}{\left(dk\right)^3+\left(dk^2\right)^3+d^3}\)
\(=\dfrac{d^3k^9+d^3k^3+d^3k^6}{d^3k^3+d^3k^6+d^3}=\dfrac{d^3\cdot k^3\left(k^6+1+k^3\right)}{d^3\cdot\left(k^3+k^6+1\right)}=k^3\)
\(=\dfrac{dk^3}{d}=\dfrac{a}{d}\)
Bài 14:
x+y+z=0
=>x+y=-z; x+z=-y; y+z=-x
\(A=\left(x+y\right)\left(y+z\right)\left(x+z\right)=\left(-z\right)\cdot\left(-x\right)\cdot\left(-y\right)\)
=-xyz
=-2

Bài 10:
Đặt \(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=k\)
=>\(\left\{{}\begin{matrix}c=dk\\b=ck=dk\cdot k=dk^2\\a=bk=dk^2\cdot k=dk^3\end{matrix}\right.\)
a:
\(\left(\dfrac{a+b+c}{b+c+d}\right)^3=\left(\dfrac{dk^3+dk^2+dk}{dk^2+dk+d}\right)^3=\left(\dfrac{dk\left(k^2+k+1\right)}{d\left(k^2+k+1\right)}\right)^3=k^3\)
\(\dfrac{a}{d}=\dfrac{dk^3}{d}=k^3\)
Do đó: \(\dfrac{a}{d}=\left(\dfrac{a+b+c}{b+c+d}\right)^3\)
b: Sửa đề: Chứng minh \(\dfrac{a^3+c^3+b^3}{c^3+b^3+d^3}=\dfrac{a}{d}\)
\(\dfrac{a^3+c^3+b^3}{c^3+b^3+d^3}=\dfrac{\left(dk^3\right)^3+\left(dk\right)^3+\left(dk^2\right)^3}{\left(dk\right)^3+\left(dk^2\right)^3+d^3}\)
\(=\dfrac{d^3k^9+d^3k^3+d^3k^6}{d^3k^3+d^3k^6+d^3}=\dfrac{d^3\cdot k^3\left(k^6+1+k^3\right)}{d^3\cdot\left(k^3+k^6+1\right)}=k^3\)
\(=\dfrac{dk^3}{d}=\dfrac{a}{d}\)

Bài 8:
a: \(\dfrac{x}{5}=\dfrac{y}{6}\)
=>\(\dfrac{x}{20}=\dfrac{y}{24}\)
\(\dfrac{y}{8}=\dfrac{z}{7}\)
=>\(\dfrac{y}{24}=\dfrac{z}{21}\)
Do đó: \(\dfrac{x}{20}=\dfrac{y}{24}=\dfrac{z}{21}=k\)
=>x=20k;y=24k;z=21k
x+y-z=69
=>20k+24k-21k=69
=>23k=69
=>k=3
=>\(x=20\cdot3=60;y=24\cdot3=72;z=21\cdot3=63\)
b: Đặt \(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=k\)
=>x=3k;y=4k;z=5k
\(2x^2+2y^2-3z^2=-100\)
=>\(2\cdot\left(3k\right)^2+2\cdot\left(4k\right)^2-3\cdot\left(5k\right)^2=-100\)
=>\(k^2=4\)
=>\(\left[{}\begin{matrix}k=2\\k=-2\end{matrix}\right.\)
TH1: k=2
=>\(x=3\cdot2=6;y=4\cdot2=8;z=5\cdot2=10\)
TH2: k=-2
=>\(x=3\cdot\left(-2\right)=-6;y=4\cdot\left(-2\right)=-8;z=5\cdot\left(-2\right)=-10\)

a, Theo tc dãy tỉ số bằng nhau
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{x-y}{3-5}=\dfrac{22}{-2}=-11\Rightarrow x=-33;y=-55\)
b, \(\dfrac{5}{2}=\dfrac{y}{x}\Rightarrow\dfrac{x}{2}=\dfrac{y}{5}\)Theo tc dãy tỉ số bằng nhau
\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=-\dfrac{21}{7}=-3\Rightarrow x=-6;y=-15\)
c, \(7x=4y\Rightarrow\dfrac{x}{4}=\dfrac{y}{7}\)Theo tc dãy tỉ số bằng nhau
\(\dfrac{x}{4}=\dfrac{y}{7}=\dfrac{x-y}{3-7}=-\dfrac{21}{-4}=7\Rightarrow x=28;y=49\)

Bài 11: \(\dfrac{2a+13b}{3a-7b}=\dfrac{2c+13d}{3c-7d}\)
=>\(\left(2a+13b\right)\left(3c-7d\right)=\left(3a-7b\right)\left(2c+13d\right)\)
=>\(6ac-14ad+39bc-91bd=6ac+39ad-14bc-91bd\)
=>-14ad-39ad=-14bc-39bc
=>ad=bc
=>\(\dfrac{a}{b}=\dfrac{c}{d}\)
Bài 12:
\(\dfrac{a+2019}{a-2019}=\dfrac{b+2020}{b-2020}\)
=>\(\left(a+2019\right)\left(b-2020\right)=\left(a-2019\right)\left(b+2020\right)\)
=>\(ab-2020a+2019b-2019\cdot2020=ab+2020a-2019b-2019\cdot2020\)
=>-2020a-2020a=-2019b-2019b
=>2020a=2019b
=>\(\dfrac{a}{2019}=\dfrac{b}{2020}\)

\(\left(x-4\right)^2\left(x+4\right)-\left(x-4\right)\left(x+4\right)^2+3\left(x^2-16\right)\)
\(=\left(x^2-16\right)\left(x-4\right)-\left(x^2-16\right)\left(x+4\right)+3\left(x^2-16\right)\)
\(=\left(x^2-16\right)\left(x-4-x-4+3\right)\)
\(=-5\left(x^2-16\right)=-5x^2+80\)

a: \(\dfrac{1}{2\text{x}5}+\dfrac{1}{5\text{x}8}+...+\dfrac{1}{14\text{x}17}\)
\(=\dfrac{1}{3}\text{x}\left(\dfrac{3}{2\text{x}5}+\dfrac{3}{5\text{x}8}+...+\dfrac{3}{14\text{x}17}\right)\)
\(=\dfrac{1}{3}\text{x}\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+...+\dfrac{1}{14}-\dfrac{1}{17}\right)\)
\(=\dfrac{1}{3}\text{x}\left(\dfrac{1}{2}-\dfrac{1}{17}\right)=\dfrac{1}{3}\text{x}\dfrac{15}{34}=\dfrac{5}{34}\)
b: \(\dfrac{1}{1\text{x}5}+\dfrac{1}{5\text{x}9}+...+\dfrac{1}{17\text{x}21}\)
\(=\dfrac{1}{4}\text{x}\left(\dfrac{4}{1\text{x}5}+\dfrac{4}{5\text{x}9}+...+\dfrac{4}{17\text{x}21}\right)\)
\(=\dfrac{1}{4}\text{x}\left(1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}+...+\dfrac{1}{17}-\dfrac{1}{21}\right)\)
\(=\dfrac{1}{4}\text{x}\left(1-\dfrac{1}{21}\right)=\dfrac{1}{4}\text{x}\dfrac{20}{21}=\dfrac{5}{21}\)
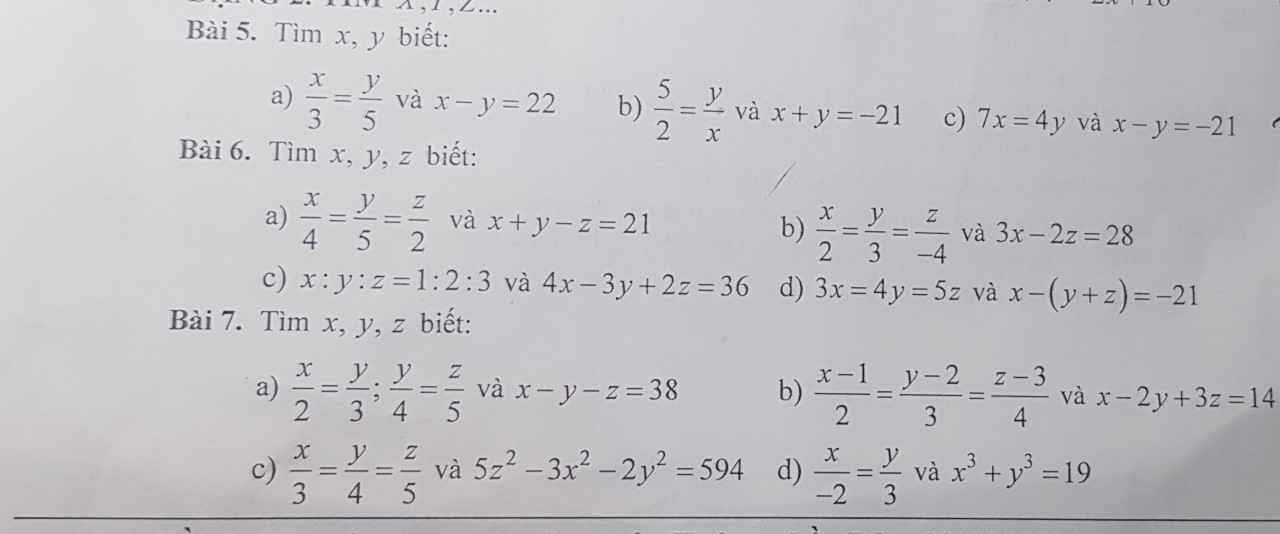
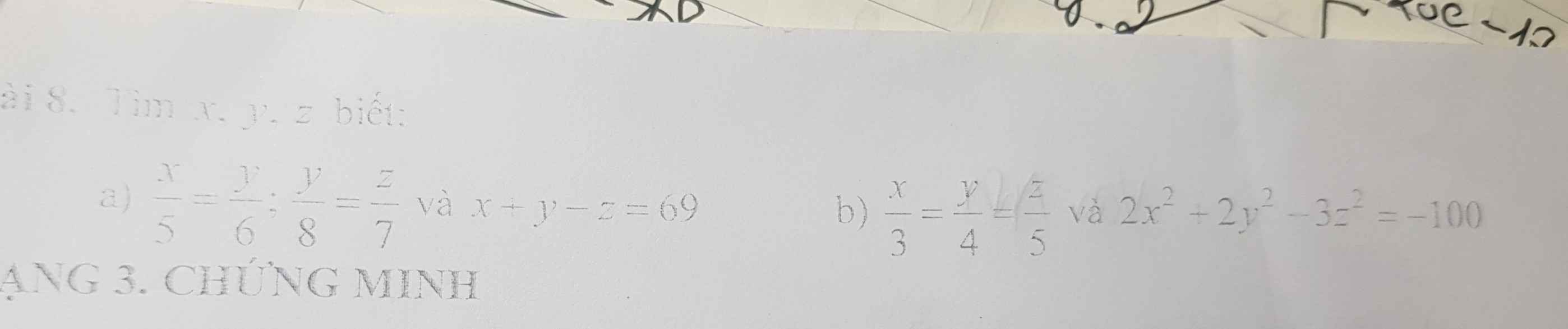

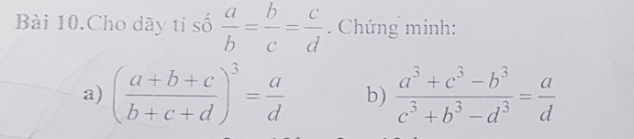
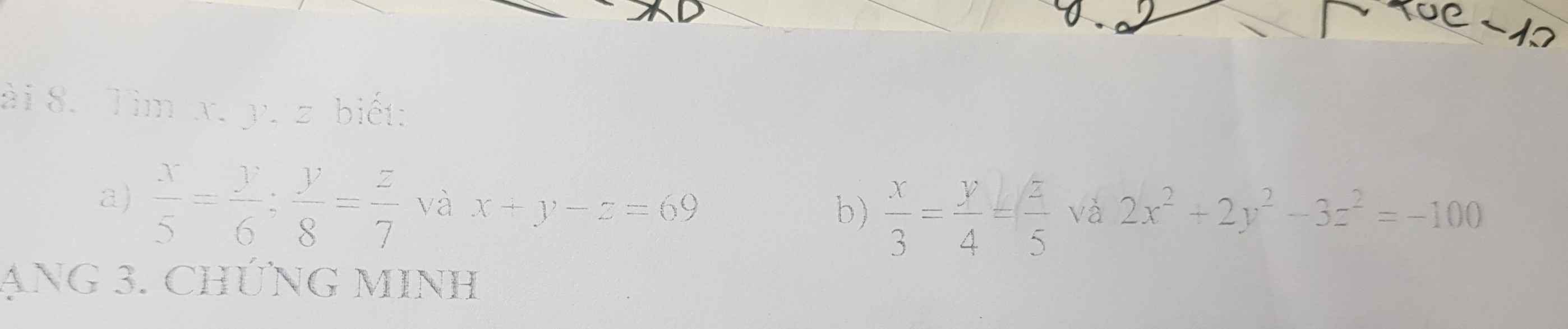
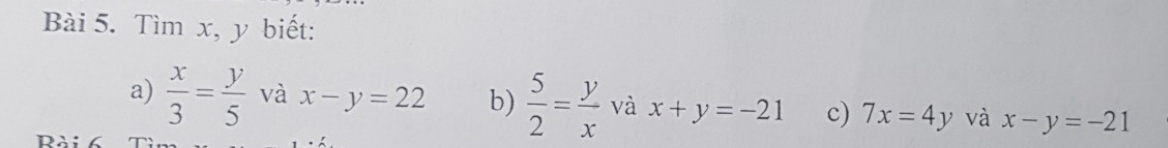
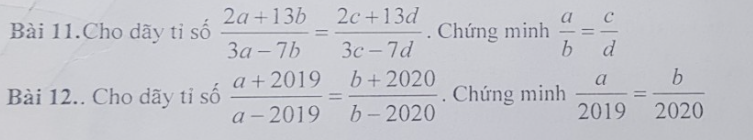
gọi x là quãng đường ab (km) (a>40)
vận tốc ô tô là \(40\times1.25\) = 50 (km/giờ)
thời gian xe máy đi được khi xe ô tô khởi hành đến khi gặp xe ô tô là \(\dfrac{x}{2\times40}\)=\(\dfrac{x}{80}\) (giờ)
thời gian xe ô tô đi được đến khi gặp xe máy là \(\dfrac{x}{2\times50}\) =\(\dfrac{x}{100}\)(giờ)
do ô tô gặp xe máy ở chính giữa đoạn đường
\(\Rightarrow\) \(\dfrac{x}{80}\) \(-\dfrac{x}{100}\)= 1
\(\Leftrightarrow\dfrac{5x}{400}-\dfrac{4x}{400}=1\)
\(\Leftrightarrow5x-4x=400\)
\(\Leftrightarrow x=400\) (thỏa mãn)
vậy quãng đường ab dìa 400 km
Gọi độ dài quãng đường AB là: `x` (km)
ĐK: x>0
Vận tốc của ô tô là: \(1,25\cdot40=50\left(km/h\right)\)
Do hai xe gặp nhau ở chính giữa đoạn đường nên ta có:
Thời gian xe máy đi thêm là: \(\left(\dfrac{1}{2}x-40\right):40=\dfrac{x}{80}-1\left(h\right)\)
Thời gian ô tô đi là: \(\dfrac{1}{2}x:50=\dfrac{x}{100}\) (h)
Do hai khoảng thời gian này bằng nhau nên ta có pt:
\(\dfrac{x}{100}=\dfrac{x}{80}-1\\ =>\dfrac{x}{80}-\dfrac{x}{100}=1\\ =>\dfrac{x}{400}=1\\ =>x=400\left(tm\right)\)
Vậy: ...