Tìm các số x,y ,z,t thoả mản:\(\left|x-y\right|+\left|y-z\right|+\left|z-t\right|+\left|t-x\right|\) = 2017
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta có : `x/4=y/5=z/7 => (3x)/12 =y/5=(2z)/14` và `2z-3x=40`
ADTC dãy tỉ số bằng nhau ta có :
` (3x)/12 =y/5=(2z)/14 =(2z-3x)/(14-12)=40/2=20`
`=> x/4=20=>x=20.4=80`
`=>y/5=20=>y=20.5=100`
`=>z/7=20=>z=20.7=140`
\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{z}{7}\)
= > \(\dfrac{3x}{12}=\dfrac{y}{5}=\dfrac{2z}{14}\) và 2z - 3x = 40
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{3x}{12}=\dfrac{y}{5}=\dfrac{2z}{14}=\dfrac{2z-32}{14-12}=\dfrac{40}{2}=20\)
\(\dfrac{x}{4}=20\Rightarrow x=80\)
\(\dfrac{y}{5}=20\Rightarrow y=100\)
\(\dfrac{z}{7}=20\Rightarrow z=140\)
Vậy 3 số x,y,z cần tìm là 80,100,140

Lời giải:
Gọi 3 phân số đó là $\frac{a}{b}, \frac{c}{d}, \frac{e}{f}$. Theo đề ta có:
$\frac{a}{b}+\frac{c}{d}+\frac{e}{f}=\frac{1}{10}(*)$
$\frac{a}{2}=\frac{c}{3}=\frac{e}{4}$
$\frac{b}{5}=\frac{d}{2}=\frac{f}{1}$
Đặt $\frac{a}{2}=\frac{c}{3}=\frac{e}{4}=k\Rightarrow a=2k; c=3k; e=4k$
Vì $\frac{b}{5}=\frac{d}{2}=\frac{f}{1}\Rightarrow b=5f; d=2f$
Khi đó, thay vào $(*)$ ta có: $\frac{2k}{5f}+\frac{3k}{2f}+\frac{4k}{f}=\frac{1}{10}$
$\Leftrightarrow \frac{59}{10}\frac{k}{f}=\frac{1}{10}$
$\Rightarrow \frac{k}{f}=\frac{1}{59}$
$\Rightarrow f=59k$
Vì $\frac{e}{f}$ là phân số tối giản nên $ƯCLN(e,f)=ƯCLN(4k,f)=1$
$\Rightarrow ƯCLN(k,f)=1$. Mà $f=59k$ nên $k=1$. Kéo theo $f=59$. Khi đó 3 phân số cần tìm là:
$\frac{2k}{5f}=\frac{2}{295}; \frac{3k}{2f}=\frac{3}{118}; \frac{4k}{f}=\frac{4}{59}$

Theo đề bài ta có :
\(\dfrac{a}{b}=\dfrac{c}{d}\)
\(\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
Đặt \(\dfrac{a}{c}=\dfrac{b}{d}=k\) ( 1 )
Theo tính chất dãy tỉ số bằng nhau ta có :
\(k=\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}\)
\(k^2=\left(\dfrac{a+b}{c+d}\right)^2=\dfrac{\left(a+b\right)^2}{\left(c+d\right)^2}\) ( 2 )
Mà từ ( 1 ) = > \(k^2=\dfrac{a}{c}.\dfrac{b}{d}=\dfrac{ab}{cd}\) ( 3 )
Từ ( 2 ) , ( 3 )
= > \(\dfrac{ab}{cd}=\dfrac{\left(a+b\right)^2}{\left(c+d\right)^2}\) ( đpcm )

A B C O P Q 1 2 2 1
a, BQ là đường phân giác của góc B
=> \(\widehat{B_1}=\widehat{B_2}=\dfrac{1}{2}\widehat{B}\) ( 1 )
CP là đường phân giác của góc C
=> \(\widehat{C_1}=\widehat{C_2}=\dfrac{1}{2}\widehat{C}\) ( 2 )
Mà tam giác ABC cân tại A
= > \(\widehat{B}=\widehat{C}\) ( 3 )
Từ ( 1 ) , ( 2 ) , ( 3 ) = > \(\widehat{B_1}=\widehat{B_2}=\widehat{C_1}=\widehat{C_2}\)
Xét tam giác OBC có :
\(\widehat{B_2}=\widehat{C_2}\) ( cmt )
= > Tam giác OBC cân tại O
b, Do O là giao của 2 đường phân giác BQ và CP của tam giác ABC
nên O là trực tâm của tam giác ABC hay điểm O cách đều 3 cạnh AB,AC, BC của tam giác ABC
c, Do O là trực tâm của tam giác ABC ( câu b, )
Mà tam giác ABC cân tại A
= > AO vừa là đường cao vừa là đường trung tuyến của tam giác ABC tức là AO đi qua trung điểm của đoạn thẳng BC
d, Xét \(\Delta QBC\) và \(\Delta PCB\) có :
\(\widehat{B_2}=\widehat{C_2}\left(cmt\right)\)
BC chung
\(\widehat{B}=\widehat{C}\left(gt\right)\)
=> \(\Delta QBC=\Delta PCB\left(g-c-g\right)\)
= > CP = BQ ( 2 cạnh tương ứng )
e, Do tam giác QBC = tam giác PCB ( câu d, )
=> BP = CQ ( 2 cạnh tương ứng )
\(P\in AB\)
= > AP + PB = AB
= > AP = AB - PB ( 4 )
\(Q\in AC\)
= > AQ + QC =AC
= > AQ = AC - QC ( 5 )
Từ ( 4 ) , ( 5 )
= > AP = AQ
Xét tam giác APQ có :
AP = AQ ( cmt )
= > Tam giác APQ cân tại A ( đpcm )
a) △���△ABC cân tại �A nên ���^=���^ABC=ACB.
Vì ��BQ và ��CP là đường phân giác của �^,�^B,C nên �1^=�2^=���^2B1=B2=2ABC, �1^=�2^=���^2C1=C2=2ACB.
Do đó �1^=�2^=�1^=�2^B1=B2=C1=C2.
Suy ra △���△OBC cân tại �O.
b) Vì �O là giao điểm các đường phân giác ��CP và ��BQ trong △���△ABC nên �O là giao điểm ba đường phân giác trong △���△ABC.
Do đó, �O cách đều ba cạnh ��,��AB,AC và ��BC.
c) Ta có △���△ABC cân tại �,��A,AO là đường phân giác của góc �A nên ��AO đồng thời là trung tuyến và đường cao của △���△ABC.
Vậy đường thẳng ��AO đi qua trung điểm của đoạn thẳng ��BC và vuông góc với nó.
d) Ta có △���=△���△PBC=△QCB (g.c.g)
⇒��=��⇒CP=BQ (hai cạnh tương ứng).
e) Ta có ��=��−��AP=AB−BP, ��=��−��AQ=AC−CQ (1);
△���=△���⇒��=��△PBC=△QCB⇒BP=CQ (2).
Lại có ��=��AB=AC (tam giác ���ABC cân tại �A) (3).
Từ (1), (2) và (3) suy ra ��=��AP=AQ.
Vậy tam giác ���APQ cân tại �A.

a)
Xét \(\Delta AOD\) và \(\Delta COB\) có: \(\left\{{}\begin{matrix}OA=OC\left(gt\right)\\\widehat{O}:chung\\OB=OD\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AOD=\Delta COB\left(c.g.c\right)\)
\(\Rightarrow AD=BC\left(\text{2 cạnh tương ứng}\right)\left(\text{đpcm}\right)\)
b)
Nối A với C
Ta có: \(\left\{{}\begin{matrix}OA=OC\\OB=OD\end{matrix}\right.\left(gt\right)\Rightarrow OA-OB=OC-OD\)
Hay \(AB=CD\)
Xét \(\Delta ABC\) và \(\Delta CDA\) có: \(\left\{{}\begin{matrix}AB=CD\left(cmt\right)\\AC:chung\\AD=BC\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABC=\Delta DCA\left(c.c.c\right)\)
\(\Rightarrow\widehat{ABC}=\widehat{CDA}\left(\text{2 góc tương ứng}\right)\)
Vì \(\Delta AOD=\Delta COB\left(cmt\right)\Rightarrow\widehat{A}=\widehat{C}\left(\text{2 góc tương ứng}\right)\)
Xét \(\Delta ABE\) và \(\Delta CDE\) có: \(\left\{{}\begin{matrix}\widehat{ABC}=\widehat{CDA}\left(cmt\right)\\AB=CD\left(cmt\right)\\\widehat{A}=\widehat{C}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABE=\Delta CDE\left(g.c.g\right)\left(\text{đpcm}\right)\)
c) Vì \(\Delta ABE=\Delta CDE\left(cmt\right)\Rightarrow AE=CE\left(\text{2 cạnh tương ứng}\right)\)
Xét \(\Delta AOE\) và \(\Delta COE\) có: \(\left\{{}\begin{matrix}OA=OC\left(gt\right)\\\widehat{A}=\widehat{C}\left(cmt\right)\\AE=CE\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AOE=\Delta COE\left(c.g.c\right)\\ \Rightarrow\widehat{AOE}=\widehat{COE}\left(\text{2 góc tương ứng}\right)\)
`=> OE` là phân giác của \(\widehat{xOy}\) (đpcm)

Vì Om là phân giác của \(\widehat{xOy}\)
\(\Rightarrow\widehat{IOE}=\widehat{IOF}=\dfrac{1}{2}\widehat{EOF}\)
Vì \(\left\{{}\begin{matrix}IE\perp Ox\\IF\perp Oy\end{matrix}\right.\left(gt\right)\Rightarrow\widehat{IEO}=\widehat{IFO}=90^o\)
Xét \(\Delta IOE\) và \(\Delta IOF\) có: \(\left\{{}\begin{matrix}\widehat{IEO}=\widehat{IFO}\left(=90^o\right)\\OI:chung\\\widehat{IOE}=\widehat{IOF}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta IOE=\Delta IOF\left(\text{cạnh huyền - góc nhọn}\right)\)
b) Vì \(\Delta IOE=\Delta IOF\left(cmt\right)\Rightarrow OE=OF\left(\text{2 cạnh tương ứng}\right)\)
Xét \(\Delta EOF\) có: \(OE=OF\left(cmt\right)\)
\(\Rightarrow\Delta EOF\) cân ở O
\(\Rightarrow\widehat{OEF}=\widehat{OFE}\)
Xét \(\Delta EOF\) có:
\(\widehat{EOF}+\widehat{OFE}+\widehat{OEF}=180^o\)
\(\Rightarrow2\widehat{EOI}+2\widehat{OEF}=180^o\\ \Rightarrow\widehat{EOI}+\widehat{OEF}=90^o\)
Gọi \(EF\cap OI\equiv M\)
Xét \(\Delta OME\) có:
\(\widehat{OEF}+\widehat{EOI}+\widehat{OME}=180^o\\ \Rightarrow90^o+\widehat{OME}=180^o\\ \Rightarrow\widehat{OME}=180^o-90^o=90^o\\ \Rightarrow EF\perp Om\left(\text{đpcm}\right)\)
Cho ���^xOy, (0∘<���^<180∘)(0∘<xOy<180∘), ��Om là tia phân giác ���^xOy. Trên tia ��Om lấy điểm �I bất kì. Gọi �,�E,F lần lượt là chân đường vuông góc kẻ từ �I đến ��Ox và ��Oy. Chứng minh:
a) △���=△���△IOE=△IOF.
b) ��⊥��EF⊥Om.
Hướng dẫn giải: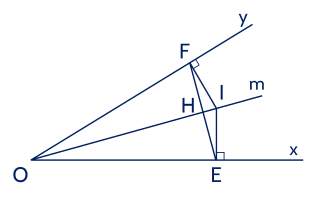
a) Xét △���△IOE và △���△IOF có
�^=�^=90∘E=F=90∘ (giả thiết);
��OI cạnh chung;
���^=���^EOI=FOI (��Om là tia phân giác).
Vậy △���=△���△IOE=△IOF (cạnh huyền - góc nhọn).
b) △���=△���△IOE=△IOF (chứng minh trên)
⇒��=��⇒OE=OF (hai cạnh tương ứng).
Gọi �H là giao điểm của ��Om và ��EF.
Xét △���△OHE và △���△OHF, có
��=��OE=OF (chứng minh trên);
���^=���^EOH=FOH (��Om là tia phân giác);
OHOH chung.
Do đó △���=△���△OHE=△OHF (c.g.c)
⇒���^=���^⇒OHE=FHO (hai góc tương ứng)
Mà ���^+���^=180∘OHE+FHO=180∘ nên ���^=���^=90∘OHE=FHO=90∘.
Vậy ��⊥��EF⊥Om.

Sửa đề bài : Chứng minh tam giác IAB = tam giác IDC
A B C I D
Xét tam giác IAD và tam giác IDC có :
\(IA=ID\) ( gt )
\(\widehat{AIB}=\widehat{DIC}\) ( 2 góc đối đỉnh )
\(IB=IC\) ( gt )
= > \(\Delta IAB=\Delta IDC\left(c-g-c\right)\)

Lời giải:
a. $A=\left\{1;2;4;7;11\right\}$
b.
Rút ngẫu nhiên 1 thẻ từ hộp, có 5 khả năng (1,2,4,7,11)
Rút được thẻ ghi số chẵn, tức là rút phải thẻ $2,4$ (2 khả năng)
Rút được thẻ ghi số nguyên tố, tức là rút phải thẻ $2,7,11$ (3 khả năng)
Xác suất để biến cố M xảy ra: $\frac{2}{5}$
Xác suất để biến cố N xảy ra: $\frac{3}{5}$

A. Ta có: $\angle BAD=\angle CAD$ $\angle ADB=120^{\circ}-\angle BAD=120^{\circ}-\angle CAD =$ $\angle ACD$ Vậy $AD$ là phân giác trong của $\angle A$ trong tam giác $ABC$ Do đó ta có $\frac{BD}{DC}=\frac{AB}{AC}$ (định lí phân giác) Mà $\angle A=\angle AHD$ (Do $H$ thuộc đường thẳng $AC$ là đường cao của tam giác $ABD$) $\angle HDA=180^{\circ}-\angle BDA=180^{\circ}-\angle B=120^{\circ}=\angle C$ Vậy $\frac{HD}{DC}=\frac{AD}{AC}=\frac{AB}{AC}=\frac{BD}{DC}$ Vậy $HD=BD$ và $\angle B=60^{\circ}=\angle HAD$ Do đó $\triangle AHD \cong \triangle ABD$ Vậy $\triangle ABC \cong \triangle AHD$ B. Ta có $\angle ADB=120^{\circ}-\angle BAD=120^{\circ}-\angle DAC=\angle ACD$ Lại có $AD$ là phân giác trong của $\angle A$ Do đó, ta có: $\frac{BD}{DC}=\frac{AB}{AC}=\frac{BD}{DA}$ Vậy $DC=DA$, vậy $AD$ là đường trung trực của $BH$ C. Ta có $\angle AHD = \angle B = 60^{\circ}=\angle HAC$, vậy $\triangle AHD \sim \triangle ACH$ Do đó $\dfrac{HA}{HD}= \dfrac{HC}{HA}$ Vậy $HA=HC$ D. Ta có $\angle ADB=120^{\circ}-\angle BAD=120^{\circ}-\angle DAC=\angle ACD$ Do đó tam giác $ABC$ cân tại $B$, ta có $DC>AB$ (Bất đẳng thức tam giác) E. Gọi $E$ là trung điểm của $CS$ thì ta có $CE=\frac{1}{2}CS$ Mà $\angle ACB=\angle AHB=90^{\circ}$, do đó $AH//CB$, ta có $\triangle AHB \sim \triangle ACB$ Vậy $\dfrac{AB}{AC}=\dfrac{HB}{BC}$ Do đó $\dfrac{HB}{AB}=\dfrac{BC}{AC}$ Vì $HEBC$ là hình bình hành nên ta có $BC=HE$ Vậy $\dfrac{HB}{AB}=\dfrac{HE}{AC}$ Lại có $\triangle HSD \sim \triangle AHC$ Vậy $\dfrac{HS}{AC}=\dfrac{HD}{AH}$ Do đó $\dfrac{HE}{AC}=\dfrac{HD+DE}{AC}=\dfrac{HD}{AC}+\dfrac{DE}{AC}$ Vì $HA=HC$ nên ta có $HD=\frac{1}{2}AC$ Vậy $\dfrac{HE}{AC}=\dfrac{1}{2}+\dfrac{DE}{AC}$ Mà $HE=\frac{1}{2}CS=\frac{1}{4}AB$ nên $\dfrac{HE}{AB}=\dfrac{1}{4}$ Do đó $\dfrac{1}{2}+\dfrac{DE}{AC}=\dfrac{1}{4}$ Vậy $\dfrac{DE}{AC}=-\dfrac{1}{4}$ Ta có $\triangle BDS \sim \triangle ACS$ Vậy $\dfrac{BD}{AC}=\dfrac{DS}{CS}$ Mà $\angle B =\angle HAD=60^{\circ} =\angle SDC$ Nên tam giác $SDC$ cũng là tam giác đều với $SD=DC$ Vậy $\dfrac{BD}{AC}=\dfrac{DS}{CS}=\dfrac{1}{2}$ Do đó $DE=\frac{-1}{4}AC$, suy ra $DE$ song song với $AC$ Lại có $\angle AHB=90^{\circ}$ nên $BH$ vuông góc với $AC$ Do đó $AD$ là đường trung trực của $BH$ nên $DE$ cũng là đường trung trực của $BH$ Vậy ta được $A,D,E$ thẳng hàng Chúc bạn học tốt! ![]()
Kẻ ��⊥��IE⊥AD (với �∈��E∈AD).
Gọi ��Ax là tia đối của tia ��AB.
Vì ���^BAC và ���^CAx là hai góc kề bù mà ���^=120∘BAC=120∘ nên ���^=60∘CAx=60∘ (1)
Ta có ��AD là phân giác của ���^⇒���^=12���^=60∘BAC⇒DAC=21BAC=60∘ (2)
Từ (1) và (2) suy ra ��AC là tia phân giác của ���^DAx
⇒��=��⇒IH=IE (tính chất tia phân giác của một góc) (3)
Vì ��DI là phân giác của ���^ADC nên ��=��IK=IE (tính chất tia phân giác của một góc) (4)
Từ (3) và (4)(4) suy ra ��=��IH=IK.
x,y,z,t là các số nguyên hay sao vậy bạn?
Vì :
| x - y | cùng tính chất chẵn lẻ với x - y
| y - z | cùng tính chất chẵn lẻ với y - z
| z - t | cùng tính chất chẵn lẻ với z - t
| t - x | cùng tính chất chẵn lẻ với t - x
\(\Rightarrow\left|x-y\right|+\left|y-z\right|+\left|z-t\right|+\left|t-x\right|\) cùng chẵn lẻ với \(\left(x-y\right)+\left(y-z\right)+\left(z-t\right)+\left(t-x\right)\)
Mà \(\left(x-y\right)+\left(y-z\right)+\left(z-t\right)+\left(t-x\right)=\left(x-x\right)+\left(y-y\right)+\left(z-z\right)+\left(t-t\right)=0\)
là số chẵn
= > \(\left|x-y\right|+\left|y-z\right|+\left|z-t\right|+\left|t-x\right|\)là số chẵn
Mà 2017 là số lẻ \(\Rightarrow\left|x-y\right|+\left|y-z\right|+\left|z-t\right|+\left|t-x\right|\ne2017\)
= > không có các số thỏa mãn