cho p:y=x2 và d:y =(1-m)x+4 tìm m để d cắt p tại 2 điểm phân biệt A(x1;x2) và B(x1;x2) sao cho y1+y2=3.(x1+x2)+12(GIÚPPPPPPPPPPPPP)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Gọi biểu thức vế trái là $A$
Áp dụng BĐT Cauchy-Schwarz:
$A+3=\frac{a+b+c+12}{a+6}+\frac{c+a+8+b+4}{b+4}+\frac{a+b+10+c+2}{c+2}$
$=(a+b+c+12)(\frac{1}{a+6}+\frac{1}{b+4}+\frac{1}{c+2})$
$\geq (a+b+c+12).\frac{9}{a+6+b+4+c+2}$
$=\frac{9(a+b+c+12)}{a+b+c+12}=9$
$\Rightarrow A\geq 6$
Ta có đpcm
Dấu "=" xảy ra khi $a+6=b+4=c+2$
Kết hợp với $a+b+c=12$ suy ra $a=2; b=4; c=6$
Lần sau bạn lưu ý gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người đọc hiểu đề của bạn hơn nhé.


\(\dfrac{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+4}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)
\(=\dfrac{\sqrt{2}+\sqrt{3}+2+2+\sqrt{6}+\sqrt{8}}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)
\(=\dfrac{\left(\sqrt{2}+\sqrt{3}+\sqrt{4}\right)\left(1+\sqrt{2}\right)}{\sqrt{2}+\sqrt{3}+\sqrt{4}}=1+\sqrt{2}\)

Lời giải:
Giả sử hai người thợ làm một mình xong việc trong lần lượt là $a$ và $b$ giờ.
Trong 1 giờ người 1 làm được $\frac{1}{a}$ công việc, người 2 làm được $\frac{1}{b}$ công việc.
Theo bài ra ta có:
\(\left\{\begin{matrix} \frac{16}{a}+\frac{16}{b}=1\\ \frac{3}{a}+\frac{6}{b}=\frac{1}{4}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} \frac{1}{a}=\frac{1}{24}\\ \frac{1}{b}=\frac{1}{48}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=24\\ b=48\end{matrix}\right.\) (giờ)

Lời giải:
$D=\frac{1}{2}\sqrt{x-1}-\frac{3}{2}\sqrt{9(x-1)}+24\sqrt{\frac{1}{64}(x-1)}$
$=\frac{1}{2}\sqrt{x-1}-\frac{3}{2}.3\sqrt{x-1}+24.\frac{1}{8}\sqrt{x-1}$
$=\frac{1}{2}\sqrt{x-1}-\frac{9}{2}\sqrt{x-1}+3\sqrt{x-1}$
$=(\frac{1}{2}-\frac{9}{2}+3)\sqrt{x-1}=-\sqrt{x-1}$
---------------
Sửa: $4x-18\to 4x-8$
$E=\sqrt{16(x-2)}+\sqrt{9(x-2)}-\sqrt{4(x-2)}$
$=4\sqrt{x-2}+3\sqrt{x-2}-2\sqrt{x-2}$
$=(4+3-2)\sqrt{x-2}=5\sqrt{x-2}$
\(D=\dfrac{1}{2}\sqrt{x-1}-\dfrac{3}{2}\sqrt{9x-9}+24\sqrt{\dfrac{x-1}{64}}\)
\(D=\dfrac{1}{2}\sqrt{x-1}-\dfrac{3}{2}\sqrt{9\left(x-1\right)}+24\dfrac{\sqrt{x-1}}{8}\)
\(D=\dfrac{1}{2}\sqrt{x-1}-\dfrac{9}{2}\sqrt{x-1}+192\sqrt{x-1}\)
\(D=\sqrt{x-1}\left(\dfrac{1}{2}-\dfrac{9}{2}+3\right)\)
\(D=-\sqrt{x-1}\)
\(E=\sqrt{16x-32}+\sqrt{9x-18}-\sqrt{4x-8}\)
\(E=\sqrt{16\left(x-2\right)}+\sqrt{9\left(x-2\right)}-\sqrt{4\left(x-2\right)}\)
\(E=4\sqrt{x-2}+3\sqrt{x-2}-2\sqrt{x-2}\)
\(E=\sqrt{x-2}\left(4+3-2\right)\)
\(E=5\sqrt{x-2}\)


Gọi giá mở cửa của hãng taxi là x(đồng)
(ĐIều kiện: x>0)
Giá mỗi km ở mức 2 là x+300(đồng)
Giá mỗi km ở mức 3 là x+300-500=x-200(đồng)
Giá mỗi km ở mức 4 là x-200-800=x-1000(đồng)
800m=0,8km
Số tiền phải trả ở mức 1 là 0,8x(đồng)
Số km đi ở mức 2 là 15-0,8=14,2
Số tiền phải trả ở mức 2 là 14,2(x+300)(đồng)
Số tiền phải trả ở mức 3 là 15(x-200)(đồng)
Số km đi ở mức 4 là: 50-30=20(km)
Số tiền phải trả ở mức 4 là 20(x-1000)(đồng)
Tổng số tiền phải trả là 481260 đồng nên ta có:
0,8x+14,2(x+300)+15(x-200)+20(x-1000)=481260
=>0,8x+14,2x+4260+15x-3000+20x-20000=481260
=>50x-18740=481260
=>50x=500000
=>x=10000(nhận)
Vậy: Giá mở cửa của taxi là 10000 đồng

Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề và hỗ trợ bạn tốt hơn nhé.
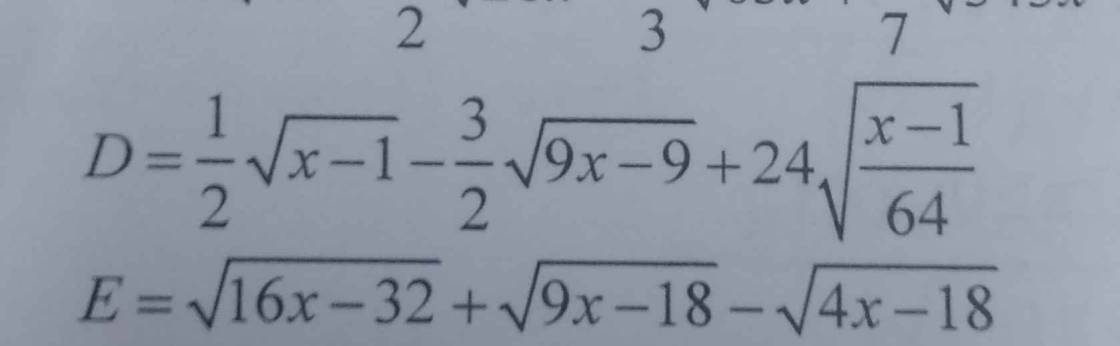


giải giúp e câu này với ạ