Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(ac=b^2\)
=>\(\dfrac{a}{b}=\dfrac{b}{c}\)
\(bd=c^2\)
=>\(\dfrac{b}{c}=\dfrac{c}{d}\)
=>\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=k\)
=>\(\left\{{}\begin{matrix}c=dk\\b=ck=dk\cdot k=dk^2\\a=bk=dk^3\end{matrix}\right.\)
\(\left(\dfrac{2a+3b-c}{2b+3c-d}\right)^3=\left(\dfrac{2\cdot dk^3+3\cdot dk^2-dk}{2\cdot dk^2+3\cdot dk-d}\right)^3\)
\(=\left(\dfrac{dk\left(2k^2+3k-1\right)}{d\left(2k^2+3k-1\right)}\right)^3=k^3\)
\(\dfrac{a}{d}=\dfrac{dk^3}{d}=k^3\)
Do đó: \(\dfrac{a}{d}=\left(\dfrac{2a+3b-c}{2b+3c-d}\right)^3\)

Gọi x (ngày) là số ngày 12 công nhân đóng xong chiếc tàu (x > 0)
Do số công nhân có năng suất làm như nhau và cùng đóng một chiếc tàu nên số công nhân và số ngày đóng xong chiếc tàu là hai đại lượng tỉ lệ nghịch
⇒ x.12 = 20.60
x.12 = 1200
x = 1200 : 12
x = 100 (nhận)
Vậy 12 công nhân đóng xong chiếc tàu trong 100 ngày
Gọi x (ngày) là số ngày 12 công nhân đóng xong chiếc tàu (x > 0)
Do số công nhân có năng suất làm như nhau và cùng đóng một chiếc tàu nên số công nhân và số ngày đóng xong chiếc tàu là hai đại lượng tỉ lệ nghịch
⇒ x.12 = 20.60
x.12 = 1200
x = 1200 : 12
x = 100 (nhận)
Vậy 12 công nhân đóng xong chiếc tàu trong 100 ngày

Gọi x (giờ) là số giờ 15 người làm cỏ xong cánh đồng (x > 0)
Do số người có cùng năng suất và cùng làm cỏ một cánh đồng nên số người và số giờ làm cỏ xong cánh đồng là hai đại lượng tỉ lệ nghịch
⇒ x.15 = 10.3
x.15 = 30
x = 30 : 15
x = 2 (nhận)
Vậy 15 người làm cỏ cánh đồng đó xong trong 2 giờ
15 người sẽ làm cỏ cánh đồng đó xong trong:
\(10\cdot3:15=2\left(giờ\right)\)

Sửa đề: x=1 là nghiệm của P(x)
\(P\left(1\right)=a\cdot1^2+b\cdot1+c=a+b+c=0\)
=>x=1 là nghiệm của P(x) khi a+b+c=0

Lời giải:
Áp dụng TCDTSBN:
$\frac{1}{x+y+z}=\frac{y+z+1}{x}=\frac{x+z+2}{y}=\frac{y+x-3}{z}=\frac{y+z+1+x+z+2+y+x-3}{x+y+z}=\frac{2(x+y+z)}{x+y+z}=2$
$\Rightarrow x+y+z=0,5$
Có:
$\frac{y+z+1}{x}=\frac{x+z+2}{y}=\frac{y+x-3}{z}=2$
$\Rightarrow \frac{y+z+1}{x}+1=\frac{x+z+2}{y}+1=\frac{y+x-3}{z}+1=3$
$\Rightarrow \frac{x+y+z+1}{x}=\frac{x+y+z+2}{y}=\frac{x+y+z-3}{z}=3$
$\Rightarrow \frac{1,5}{x}=\frac{2,5}{y}=\frac{-2,5}{z}=3$
$\Rightarrow x=0,5; y=\frac{5}{6}; z=\frac{-5}{6}$

Thay \(x=3\) vào đk đề cho, ta có:
\(4f\left(3\right)=0\Leftrightarrow f\left(3\right)=0\) \(\Rightarrow\) \(x=3\) là một nghiệm của \(f\left(x\right)\)
Thay \(x=-1\) vào đk đề cho, ta có:
\(-4f\left(-3\right)=0\) \(\Leftrightarrow f\left(-3\right)=0\) \(\Rightarrow x=-3\) là một nghiệm khác của \(f\left(x\right)\)
\(\Rightarrow f\left(x\right)\) có ít nhất 2 nghiệm (đpcm)

Biến cố có xác suất cao nhất mình có thể nghĩ ra là biến cố: "Lấy ra được một quả bóng không phải là bóng màu xanh." Xác suất đó lên tới \(\dfrac{4}{5}\).
Hoặc có thể là "Bóng được chọn không có màu đen." đây là biến cố chắc chắn (xác suất 100%). Bạn cần phải bổ sung thêm cho điều kiện đề bài nhé.

a: ta có: \(AE=EB=\dfrac{AB}{2}\)
\(AD=DC=\dfrac{AC}{2}\)
mà AB=AC
nên AE=EB=AD=DC
Xét ΔEBC và ΔDCB có
EB=DC
\(\widehat{EBC}=\widehat{DCB}\)(ΔABC cân tại A)
BC chung
Do đó: ΔEBC=ΔDCB
=>BD=CE
b: Ta có: ΔEBC=ΔDCB
=>\(\widehat{ECB}=\widehat{DBC}\)
=>\(\widehat{GBC}=\widehat{GCB}\)
=>ΔGBC cân tại G
c: Xét ΔABC có
BD,CE là các đường trung tuyến
BD cắt CE tại G
Do đó: G là trọng tâm của ΔABC
=>\(BG=\dfrac{2}{3}BD;CG=\dfrac{2}{3}CE\)
Vì \(BG=\dfrac{2}{3}BD\)
nên \(DG=\dfrac{1}{2}BG\)
Vì \(CG=\dfrac{2}{3}CE\)
nên \(EG=\dfrac{1}{2}CG\)
Xét ΔGBC có GB+GC>BC
=>\(2\left(EG+GD\right)>BC\)
=>\(GE+GD>\dfrac{BC}{2}\)

\(\dfrac{4,3}{a}=\dfrac{7,7}{b}=3\)
Áp dụng tính chất dãy tí số bằng nhau ta có:
\(\dfrac{4,3}{a}=\dfrac{7,7}{b}=\dfrac{4,3+7,7}{a+b}=\dfrac{12}{a+b}=3\)
\(\Rightarrow a+b=\dfrac{12}{3}\)
\(\Rightarrow a+b=4\)
Điền vào số 4
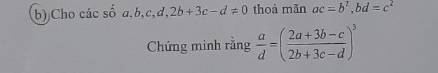
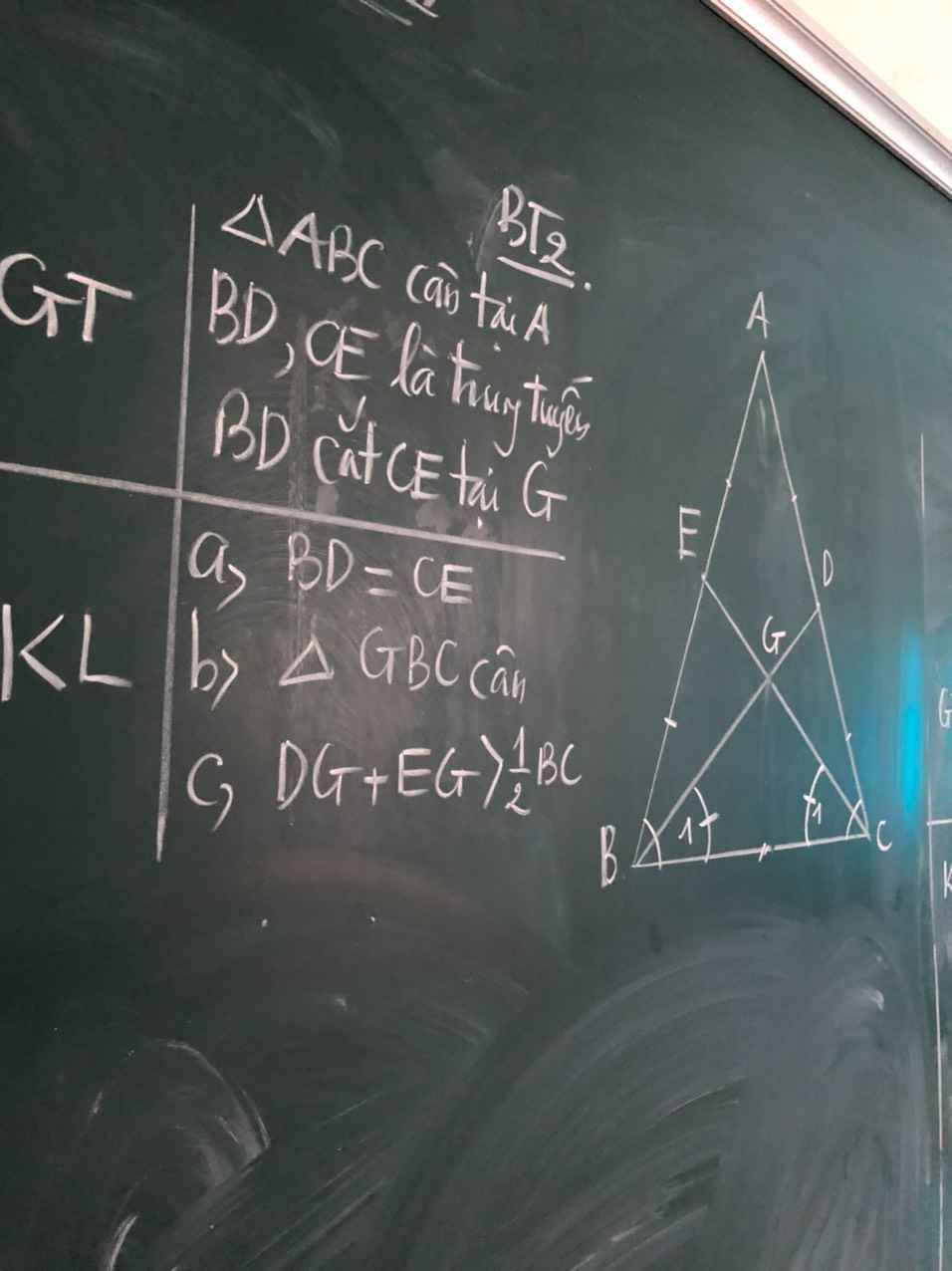
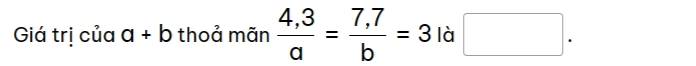
Lời giải:
$ac=b^2\Rightarrow \frac{a}{b}=\frac{b}{c}$
$bd=c^2\Rightarrow \frac{b}{c}=\frac{c}{d}$
$\Rightarrow \frac{a}{b}=\frac{b}{c}=\frac{c}{d}$
Đặt $\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=k\Rightarrow a=bk; b=ck; c=dk$
Khi đó:
$\frac{a}{d}=\frac{bk}{d}=\frac{ck^2}{d}=\frac{dk^3}{d}=k^3(1)$
Lại có:
$(\frac{2a+3b-c}{2b+3c-d})^3=(\frac{2bk+3b-c}{2ck+3c-d})^3=(\frac{2ck^2+3ck-c}{2dk^2+3dk-d})^3$
$=[\frac{c(2k^2+3k-1)}{d(2k^2+3k-1)}]^3=(\frac{c}{d})^3=(\frac{dk}{d})^3=k^3(2)$
Từ $(1); (2)$ ta có đpcm.