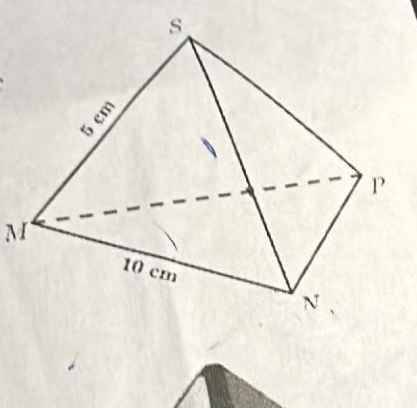
 tính các độ dài các cạnh còn lại của hình chóp . Xác định số đo các của góc tam giác mnp
tính các độ dài các cạnh còn lại của hình chóp . Xác định số đo các của góc tam giác mnp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(HB=\dfrac{12^2}{16}=9\left(cm\right)\)
BC=BH+CH=9+16=25(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=\sqrt{9\cdot25}=15\left(cm\right)\\AC=\sqrt{16\cdot25}=20\left(cm\right)\end{matrix}\right.\)

a: Ta có: \(AM=MB=\dfrac{AB}{2}\)
\(DN=NC=\dfrac{DC}{2}\)
\(BE=EC=\dfrac{BC}{2}\)
mà AB=DC=BC
nên AM=MB=DN=NC=BE=EC
Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
b: Xét ΔMBC vuông tại B và ΔECD vuông tại C có
MB=EC
BC=CD
Do đó: ΔMBC=ΔECD
=>\(\widehat{BMC}=\widehat{CED}\)
=>\(\widehat{CED}+\widehat{ECM}=90^0\)
=>CM\(\perp\)DE
c: ΔMBC=ΔECD
=>MC=ED

a: ĐKXĐ: \(x\notin\left\{-1;0;1\right\}\)
\(\dfrac{x+3}{x+1}-\dfrac{x-1}{x}=\dfrac{3x^2+4x+1}{x\left(x-1\right)}\)
=>\(\dfrac{x\left(x+3\right)-\left(x-1\right)\left(x+1\right)}{x\left(x+1\right)}=\dfrac{3x^2+4x+1}{x\left(x-1\right)}\)
=>\(\dfrac{x^2+3x-x^2+1}{\left(x^2+x\right)}=\dfrac{3x^2+4x+1}{x\left(x-1\right)}\)
=>\(\dfrac{\left(3x+1\right)\left(x-1\right)}{x\left(x+1\right)\left(x-1\right)}=\dfrac{\left(3x^2+4x+1\right)\left(x+1\right)}{x\left(x-1\right)\left(x+1\right)}\)
=>\(\left(3x^2+4x+1\right)\left(x+1\right)=\left(3x+1\right)\left(x-1\right)\)
=>\(\left(3x+1\right)\left(x^2+2x+1\right)-\left(3x+1\right)\left(x-1\right)=0\)
=>\(\left(3x+1\right)\left(x^2+2x+1-x+1\right)=0\)
=>\(\left(3x+1\right)\left(x^2+x+2\right)=0\)
mà \(x^2+x+2=\left(x+\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0\forall x\)
nên 3x+1=0
=>\(x=-\dfrac{1}{3}\left(nhận\right)\)
b: ĐKXĐ: \(x\notin\left\{-3;-1\right\}\)
\(\dfrac{x}{2\left(x+3\right)}+\dfrac{x}{2x+2}=\dfrac{-x}{\left(x+1\right)\left(x+3\right)}\)
=>\(\dfrac{x}{2\left(x+3\right)}+\dfrac{x}{2\left(x+1\right)}=\dfrac{-x}{\left(x+1\right)\left(x+3\right)}\)
=>\(\dfrac{x\left(x+1\right)+x\left(x+3\right)}{2\left(x+3\right)\left(x+1\right)}=\dfrac{-2x}{2\left(x+1\right)\left(x+3\right)}\)
=>\(x^2+x+x^2+3x=-2x\)
=>\(2x^2+6x=0\)
=>2x(x+3)=0
=>x(x+3)=0
=>\(\left[{}\begin{matrix}x=0\left(nhận\right)\\x=-3\left(nhận\right)\end{matrix}\right.\)
c: ĐKXĐ: \(x\notin\left\{0;\dfrac{3}{2}\right\}\)
\(\dfrac{1}{2x-3}=\dfrac{3}{2x^2-3x}+\dfrac{x}{5}\)
=>\(\dfrac{x-3}{x\left(2x-3\right)}=\dfrac{x}{5}\)
=>\(x^2\left(2x-3\right)=5\left(x-3\right)\)
=>\(2x^3-3x^2-5x+15=0\)
=>\(x\simeq-1,9\left(nhận\right)\)
d: ĐKXĐ: \(x\notin\left\{0;-2\right\}\)
\(\dfrac{x+2}{x}=\dfrac{x^2+5x+4}{x^2+2x}+\dfrac{x}{x+2}\)
=>\(\dfrac{\left(x+2\right)^2}{x\left(x+2\right)}=\dfrac{x^2+5x+4}{x\left(x+2\right)}+\dfrac{x^2}{x\left(x+2\right)}\)
=>\(\left(x+2\right)^2=x^2+5x+4+x^2\)
=>\(2x^2+5x+4-x^2-4x-4=0\)
=>\(x^2+x=0\)
=>x(x+1)=0
=>\(\left[{}\begin{matrix}x=0\left(loại\right)\\x=-1\left(nhận\right)\end{matrix}\right.\)

\(x^4+1997x^2+1996x+1997\)
\(=\left(x^4+x^3+x^2\right)+\left(-x^3-x^2-x\right)+\left(1997x^2+1997x+1997\right)\)
\(=x^2\left(x^2+x+1\right)-x\left(x^2+x+1\right)+1997\left(x^2+x+1\right)\)
\(=\left(x^2+x+1\right)\left(x^2-x+1997\right)\)

4(x-2)-3(x+1)=5
=>\(4x-8-3x-3=5\)
=>\(x-11=5\)
=>x=11+5=16
\(4\left(x-2\right)-3\left(x+1\right)=5\)
\(\Leftrightarrow4x-8-3x-3=5\)
\(\Leftrightarrow\left(4x-3x\right)=5+8+3\)
\(\Leftrightarrow x=16\)
Vậy \(x=16\)

\(sin^210+sin^220+sin^245+sin^270+sin^280\)
\(=sin^210+sin^220+sin^245+cos^220+cos^210=1+1+sin^245=2+\dfrac{1}{2}=\dfrac{5}{2}\)

\(sin^210^0+sin^220^0+sin^245^0+sin^270^0+sin^280^0\)
\(=\left(sin^210^0+sin^280^0\right)+\left(sin^220^0+sin^270^0\right)+\left(sin^245^0\right)\)
\(=\left(sin^210^0+cos^210^0\right)+\left(sin^220^0+cos^220^0\right)+\left(\dfrac{1}{2}\right)\)
\(=1+1+\dfrac{1}{2}=\dfrac{5}{2}\)

\(x^3+5x^2+8x+4\)
\(=x^3+x^2+4x^2+4x+4x+4\)
\(=x^2\left(x+1\right)+4x\left(x+1\right)+4\left(x+1\right)\)
\(=\left(x+1\right)\left(x^2+4x+4\right)\)
\(=\left(x+1\right)\left(x+2\right)^2\)

\(\text{Sửa đề }:x^4-3x+2=(x-1)(x^3+ax^2+bx-2)\\\Leftrightarrow x^4-x^3+x^3-x^2+x^2-x-2x+2=(x-1)(x^3+ax^2+bx-2)\\\Leftrightarrow x^3(x-1)+x^2(x-1)+x(x-1)-2(x-1)=(x-1)(x^3+ax^2+bx-2)\\\Leftrightarrow (x-1)(x^3+x^2+x-2)=(x-1)(x^3+ax^2+bx-2)\\\Rightarrow a=b=1\)
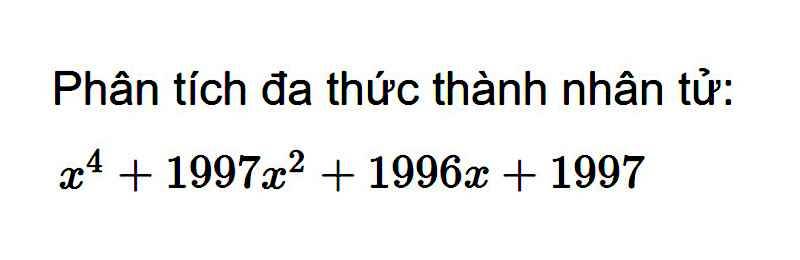

Vì \(S.MNP\) là hình chóp tam giác đều
nên \(SM=SN=SP=5\left(cm\right)\) và \(\triangle MNP\) đều (t/c)
\(\Rightarrow\left\{{}\begin{matrix}MN=NP=PM=10\left(cm\right)\\\widehat{MNP}=\widehat{NPM}=\widehat{PMN}=60^{\circ}\end{matrix}\right.\)