Một hình chữ nhật có chu vi 21,6 dm,chiều rộng bằng 80% chiều dài.Tính diện tích của hình chữ nhật đó?
GIÚP MÌNH VỚI, MÌNH ĐANG CẦN GẤP!!!!!!!!!!!!!!!!!!!!!
SẮP ĐẾN HAI GIỜ RỒI, GIÚP MÌNH VỚI!!!!!!!!!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

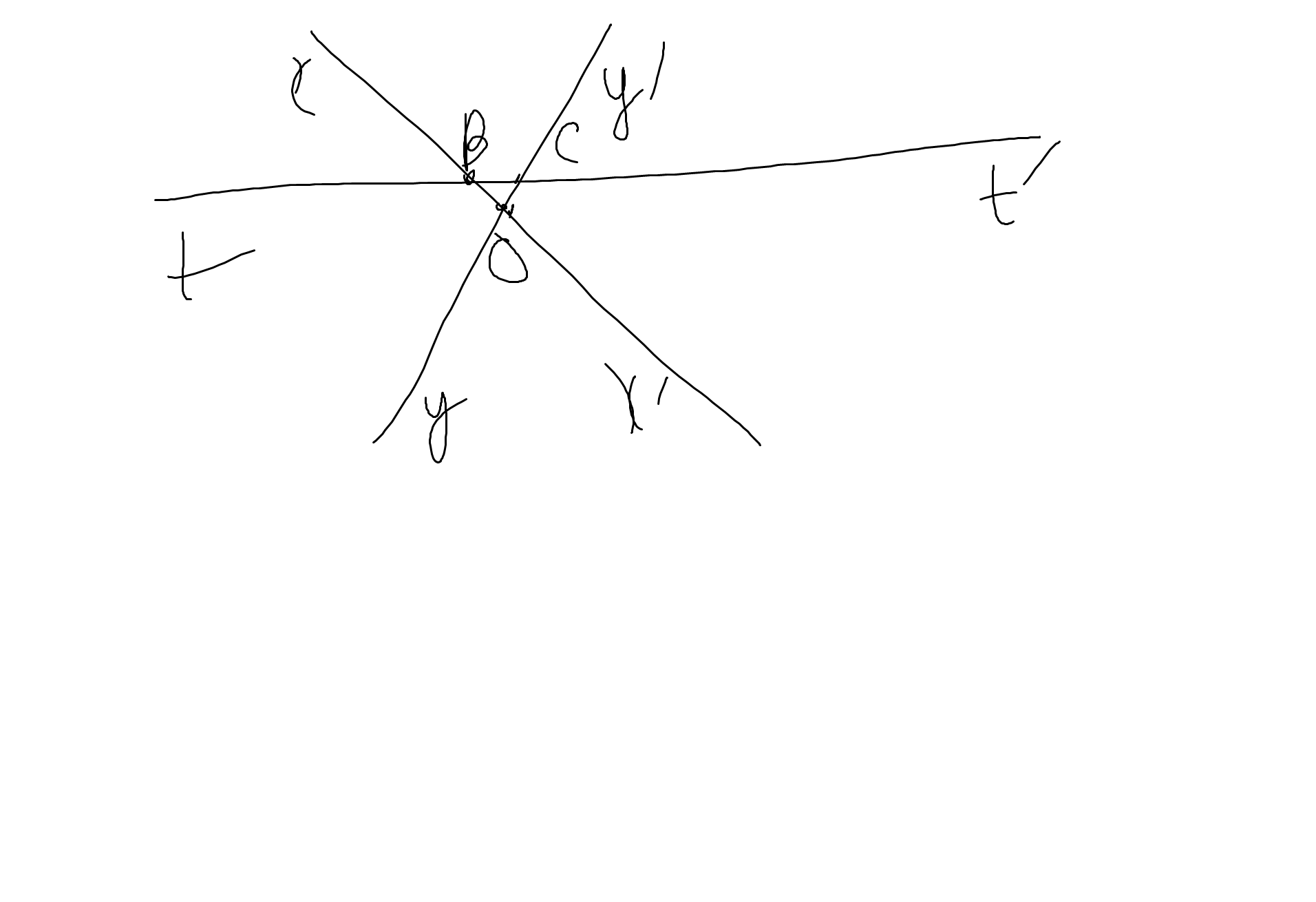
Bài 3: Các cặp góc so le trong là: \(\widehat{tBO};\widehat{BOC}\); \(\widehat{OBC};\widehat{yOB}\); \(\widehat{BCO};\widehat{x'OC}\); \(\widehat{t'CO};\widehat{BOC}\)
Các cặp góc đồng vị là:
\(\widehat{xBt};\widehat{xOy}\); \(\widehat{tBO};\widehat{x'Oy}\); \(\widehat{y'Ct'};\widehat{x'Oy'}\); \(\widehat{t'CO};\widehat{x'Oy}\)
Bài 2:
Các cặp góc so le trong là \(\widehat{FEC};\widehat{ACB}\)
Các cặp góc đồng vị là \(\widehat{ADE};\widehat{ABC}\); \(\widehat{AED};\widehat{ACB}\)
Các cặp góc trong cùng phía là: \(\widehat{BDE};\widehat{B}\); \(\widehat{DEC};\widehat{ECB}\)

\(x^3+ax+b\\ =\left(x^3+4x^2+3x\right)+\left(-4x^2-16x-12\right)+\left(a+13\right)x+\left(b+12\right)\\ =x\left(x^2+4x+3\right)-4\left(x^2+4x+3\right)+\left(a+13\right)x+\left(b+12\right)\\ =\left(x-4\right)\left(x^2+4x+3\right)+\left(a+13\right)x+\left(b+12\right)\)
Để `x^3+ax+b` chia hết cho `x^2+4x+3` thì:
\(\left\{{}\begin{matrix}a+13=0\\b+12=0\end{matrix}\right.=>\left\{{}\begin{matrix}a=-13\\b=-12\end{matrix}\right.\)

`x (2x - 9) = 3x(x - 5) `
`<=> 2x^2 - 9x = 3x^2 - 15x`
`<=> 3x^2 - 2x^2 - 15x + 9x =0`
`<=> x^2 - 6x = 0`
`<=> x(x-6) = 0`
`<=> x = 0` hoặc `x - 6 = 0`
`<=> x = 0` hoặc `x = 6`
Vậy ....

\(\left(4x+2\right)\left(x^2+1\right)=0\)(1)
Ta có: `x^2>=0` với mọi x
`=>x^2+1>=1>0` với mọi x
`=>x^2+1≠0`
\(\left(1\right)\Leftrightarrow4x+2=0\\ \Leftrightarrow4x=-2\\ \Leftrightarrow x=-\dfrac{2}{4}=-\dfrac{1}{2}\)
`(4x + 2)(x^2 + 1) = 0`
Trường hợp 1:
`4x + 2 = 0`
`<=> 4x = -2`
`<=> x =` \(-\dfrac{1}{2}\)
Trường hợp 2:
`x^2 + 1 = 0`
`<=> x^2 = -1` (Không tồn tại `x`)
Vậy `x =` \(-\dfrac{1}{2}\)

\(g.x^3-3x^2+3x-1=0\\ \Leftrightarrow\left(x-1\right)^3=0\\ \Leftrightarrow x-1=0\\ \Leftrightarrow x=1\\ h.x\left(2x-7\right)-4x+14=0\\ \Leftrightarrow x\left(2x-7\right)-2\left(2x-7\right)=0\\ \Leftrightarrow\left(2x-7\right)\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x=7\\x=2\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=2\end{matrix}\right.\\ k.\left(2x-5\right)^2\left(x+2\right)^2=0\\ \Leftrightarrow\left[{}\begin{matrix}2x-5=0\\x+2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}2x=5\\x=-2\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-2\end{matrix}\right.\\ l.x\left(2x-9\right)=3x\left(x-5\right)\\ \Leftrightarrow3x^2-15x-2x^2+9x=0\\ \Leftrightarrow x^2-6x=0\\ \Leftrightarrow x\left(x-6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=6\end{matrix}\right.\\ m.\left(x^2-2x+1\right)-4=0\\ \Leftrightarrow\left(x-1\right)^2=2^2\\ \Leftrightarrow\left[{}\begin{matrix}x-1=2\\x-1=-2\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=2+1=3\\x=-2+1=-1\end{matrix}\right.\)
a: (3x-2)(4x+5)=0
=>\(\left[{}\begin{matrix}3x-2=0\\4x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{5}{4}\end{matrix}\right.\)
c: \(\left(4x+2\right)\left(x^2+1\right)=0\)
mà \(x^2+1>=1>0\forall x\)
nên 4x+2=0
=>4x=-2
=>\(x=-\dfrac{1}{2}\)
d: (2x+7)(x-5)(5x+1)=0
=>\(\left[{}\begin{matrix}2x+7=0\\x-5=0\\5x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{7}{2}\\x=5\\x=-\dfrac{1}{5}\end{matrix}\right.\)
f: \(\left(x^2-4\right)\left(x-2\right)\left(3-2x\right)=0\)
=>\(\left(x-2\right)^2\cdot\left(x+2\right)\left(3-2x\right)=0\)
=>\(\left[{}\begin{matrix}x-2=0\\x+2=0\\3-2x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\\x=\dfrac{3}{2}\end{matrix}\right.\)

Từ 2 đến 201 số lượng số hạng là: (201 - 2) : 1 + 1 = 200 (số hạng)
Số lượng cặp là: 200 : 2 = 100 (cặp)
1 - 2 + 3 - 4 + 5 - ... + 199 - 200 + 201
= 1 + (-2 + 3) + (-4 + 5) + ... + (-198 + 199) + (-200 + 201)
= 1 + 1 + 1 + ... + 1 + 1
= 1 + 100*1
= 1 + 100
= 101

b: Vì 2n+1;2n+2;2n+3 là ba số tự nhiên liên tiếp
nên \(\left(2n+1\right)\left(2n+2\right)\left(2n+3\right)⋮3\)

Ta có:
\(1+2+3+...+n\)
Số lượng số hạng là: `(n-1):1+1=n` (số hạng)
Tổng của dãy số là: `(n+1)*n/2`
Áp dụng ta có:
\(\dfrac{1}{1+2+3}+\dfrac{1}{1+2+3+4}+....+\dfrac{1}{1+2+3+...+100}\\ =\dfrac{1}{\dfrac{3\cdot\left(3+1\right)}{2}}+\dfrac{1}{\dfrac{4\cdot\left(4+1\right)}{2}}+...+\dfrac{1}{\dfrac{100\cdot\left(100+1\right)}{2}}\\ =\dfrac{2}{3\cdot4}+\dfrac{2}{4\cdot5}+...+\dfrac{2}{100\cdot101}\\ =2\left(\dfrac{1}{3\cdot4}+\dfrac{1}{4\cdot5}+...+\dfrac{1}{100\cdot101}\right)\\ =2\left(\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{100}-\dfrac{1}{101}\right)\\ =2\left(\dfrac{1}{3}-\dfrac{1}{101}\right)\\ =2\cdot\dfrac{98}{303}\\ =\dfrac{196}{303}\)
Tổng chiều dài và rộng của hình chữ nhật là:
`21,6 : 2 = 10,8 (dm)`
Đổi `80% =` \(\dfrac{4}{5}\)
Ta có sơ đồ:
Chiều dài: (5 phần)
Chiều rộng: (4 phần)
Tổng số phần bằng nhau là:
`5+4 = 9` (phần)
Giá trị 1 phần là:
`10,8 : 9 = 1,2 (dm)`
Chiều dài hình chữ nhật:
`1,2` x `5 = 6 (dm)`
Chiều rộng hình chữ nhật là:
`10,8 - 6 = 4,8 (dm)`
Diện tích hình chữ nhật là:
`6` x `4,8 = 28,8 (dm^2)`
Đáp số: `28,8 dm^2`