\(\dfrac{5}{9}\cdot\dfrac{13}{28}+\dfrac{13}{28}\cdot\dfrac{4}{9}\\ =\dfrac{13}{28}\cdot\left(\dfrac{5}{9}+\dfrac{4}{9}\right)\\=\dfrac{13}{28}\cdot\dfrac{9}{9}\\ =\dfrac{13}{28}\cdot1\\ =\dfrac{13}{28}\)

$\frac59\times\frac{13}{28}+\frac{13}{28}\times\frac49$

$=\frac{13}{28}\times\left(\frac59+\frac49\right)$

$=\frac{13}{28}\times1=\frac{13}{28}$

ĐKXĐ: \(x\ne-1\)

\(\dfrac{-7^2+4}{x^3+1}=\dfrac{5}{x^2-x+1}-\dfrac{1}{x+1}\) (sửa đề)

\(\Leftrightarrow\dfrac{-45}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{5\left(x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}-\dfrac{x^2-x+1}{\left(x+1\right)\left(x^2-x+1\right)}\)

\(\Rightarrow-45=5x+5-x^2+x-1\)

\(\Leftrightarrow-45=-x^2+6x+4\)

\(\Leftrightarrow x^2-6x-49=0\)

\(\Leftrightarrow\left(x-3\right)^2-58=0\)

\(\Leftrightarrow\left(x-3-\sqrt{58}\right)\left(x-3+\sqrt{58}\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=3+\sqrt{58}\left(tm\right)\\x=3-\sqrt{58}\left(tm\right)\end{matrix}\right.\)

P/s: Bài này phải lớp 8, 9 mới học đến nhé.

Sửa đề: \(\dfrac{-7x^2+4}{x^3+1}=\dfrac{5}{x^2+x+1}-\dfrac{1}{x+1}\)

ĐKXĐ: x<>-1

\(\dfrac{-7x^2+4}{x^3+1}=\dfrac{5}{x^2+x+1}-\dfrac{1}{x+1}\)

=>\(\dfrac{-7x^2+4}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{5\left(x+1\right)-x^2-x-1}{\left(x+1\right)\left(x^2+x+1\right)}\)

=>\(-7x^2+4=5x+5-x^2-x-1\)

=>\(-7x^2+4=-x^2+4x+4\)

=>\(-7x^2+x^2-4x=0\)

=>\(-6x^2-4x=0\)

=>\(3x^2+2x=0\)

=>x(3x+2)=0

=>\(\left[{}\begin{matrix}x=0\left(nhận\right)\\x=-\dfrac{2}{3}\left(nhận\right)\end{matrix}\right.\)

a) \(A=\dfrac{2x-1}{x+2}=\dfrac{2x+4-5}{x+2}=2-\dfrac{5}{x+2}\)

Để A là số nguyên thì 5 ⋮ x + 2

=> x + 2 ∈ Ư(5) = {1; -1; 5; -5} 

=> x ∈ {-1; -3; 3; -7}

b) Để A là số tự nhiên thì \(A\ge0\Rightarrow\dfrac{2x-1}{x+2}\ge0\Rightarrow-2\le x\le\dfrac{1}{2}\) 

Mà x nguyên nên x = - 1 

c) x là số tự nhiên để A nguyên ⇒ x = 3 

d) x nguyên lớn nhất để A nguyên => x = 3 

e) x nguyên nhỏ nhất để A nguyên => x = -7

a: Để A là số nguyên thì \(2x-1⋮x+2\)

=>\(2x+4-5⋮x+2\)

=>\(-5⋮x+2\)

=>\(x+2\in\left\{1;-1;5;-5\right\}\)

=>\(x\in\left\{-1;-3;3;-7\right\}\)

b: Khi x=-1 thì \(A=\dfrac{2\cdot\left(-1\right)-1}{-1+2}=-3\notin N\)

=>Loại

Khi x=-3 thì \(A=\dfrac{2\left(-3\right)-1}{-3+2}=\dfrac{-7}{-1}=7\in N\)

=>Nhận

Khi x=3 thì \(A=\dfrac{2\cdot3-1}{3+2}=\dfrac{5}{5}=1\in N\)

=>Nhận

Khi x=-7 thì \(A=\dfrac{2\cdot\left(-7\right)-1}{-7+2}=\dfrac{-15}{-5}=3\in N\)

=>Nhận

c: Để A nguyên thì \(x\in\left\{-1;-3;3;-7\right\}\)

mà x>=0

nên x=3

d: Để A nguyên thì \(x\in\left\{-1;-3;3;-7\right\}\)

mà x là số nguyên lớn nhất

nên x=3

e: Để A nguyên thì \(x\in\left\{-1;-3;3;-7\right\}\)

mà x là số nguyên nhỏ nhất

nên x=-7

\(8\cdot\left(-125\right)=-\left(8\cdot125\right)=-1000\)

8 x (-125) = -(8 x 125) = -1000 

Điểm trung bình là:

\(\dfrac{6+8+10+8\cdot2+7\cdot3}{3+2+3}=\dfrac{24+16+21}{8}\simeq7,6\)

2,5+3,2+2,7

=5,7+2,7

=8,4

\(\left[-1,5\right]-\dfrac{1}{5}=-\dfrac{3}{2}-\dfrac{1}{5}=-\dfrac{15}{10}-\dfrac{2}{10}=-\dfrac{17}{10}\)

`#3107.101107`

`2,5 + 3,2 + 2,7`

`= 5,7 + 2,7`

`= 8,4`

____

$-1,5 - \dfrac{1}{5}$

`= -1,5 - 0,2`

`= -1,7`

Ta có: \(\dfrac{y+z+2}{x}=\dfrac{x+z+3}{y}=\dfrac{x+y-5}{z}=\dfrac{1}{x+y+z}\) (\(x,y,z\ne0\))

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{y+z+2}{x}=\dfrac{x+z+3}{y}=\dfrac{x+y-5}{z}=\dfrac{1}{x+y+z}\)

\(=\dfrac{y+z+2+x+z+3+x+y-5}{x+y+z}=\dfrac{2\left(x+y+z\right)}{x+y+z}=2\)

\(\Rightarrow\left\{{}\begin{matrix}y+z+2=2x\\x+z+3=2y\\x+y-5=2z\\x+y+z=\dfrac{1}{2}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x+y+z+2=3x\\x+y+z+3=3y\\x+y+z-5=3z\\x+y+z=\dfrac{1}{2}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}3x=\dfrac{1}{2}+2=\dfrac{5}{2}\\3y=\dfrac{1}{2}+3=\dfrac{7}{2}\\3z=\dfrac{1}{2}-5=-\dfrac{9}{2}\\x+y+z=\dfrac{1}{2}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{6}\left(tm\right)\\y=\dfrac{7}{6}\left(tm\right)\\z=-\dfrac{3}{2}\left(tm\right)\end{matrix}\right.\)

#$\mathtt{Toru}$

ai giải dc mình tick cho

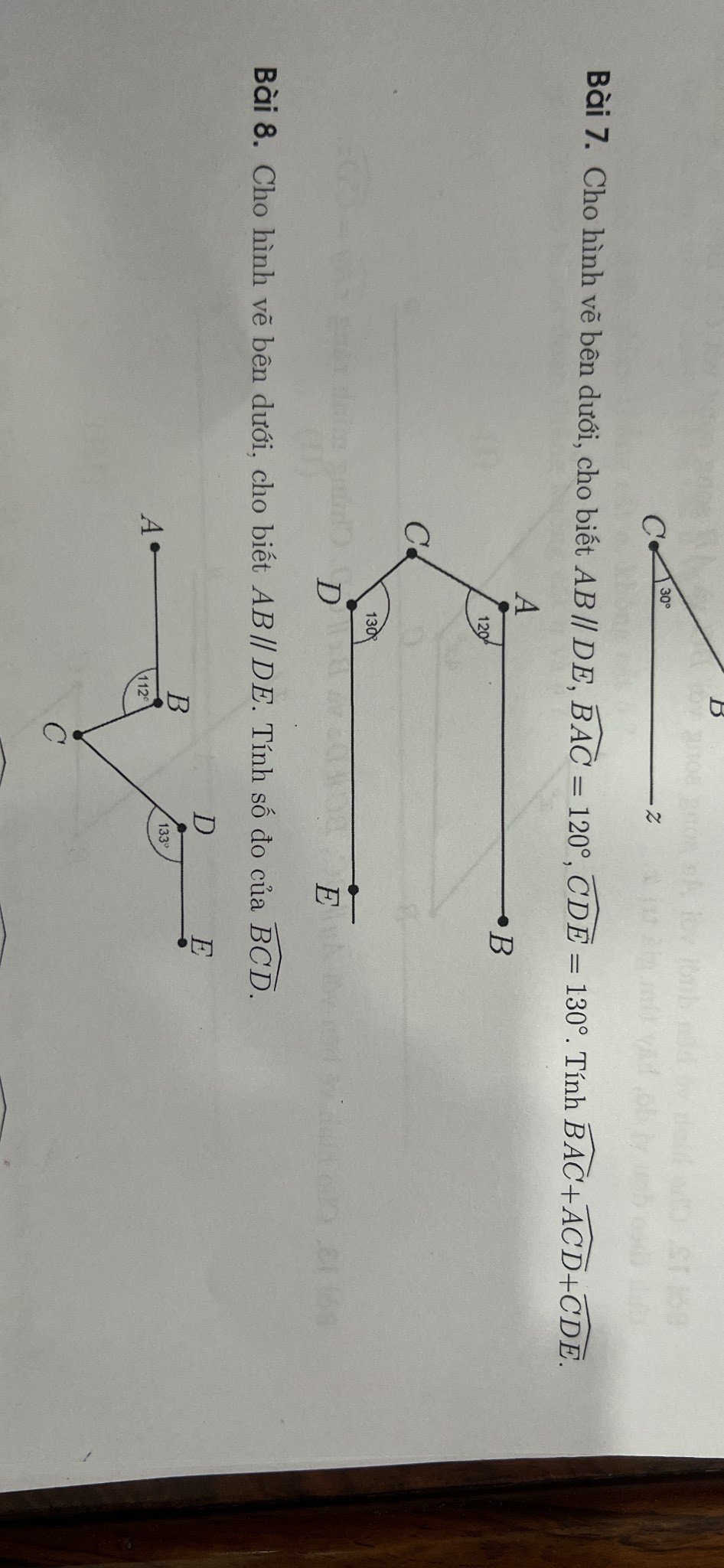
Bài 7: Kẻ CF//AB//DE(CF,AB cùng nằm trên nửa mặt phẳng bờ AC)

CF//AB

=>\(\widehat{BAC}+\widehat{ACF}=180^0\)

CF//DE

=>\(\widehat{FCD}+\widehat{CDE}=180^0\)

\(\widehat{BAC}+\widehat{ACF}+\widehat{FCD}+\widehat{CDE}\)

\(=180^0+180^0=360^0\)

=>\(\widehat{BAC}+\widehat{ACD}+\widehat{CDE}=360^0\)

Bài 8:

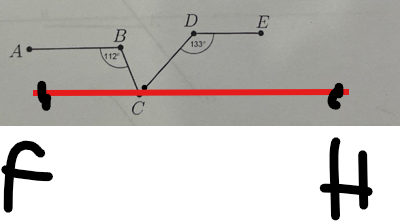
Qua C, kẻ FH//AB//DE

FC//AB

=>\(\widehat{ABC}+\widehat{FCB}=180^0\)

=>\(\widehat{FCB}=68^0\)

Ta có: CH//DE

=>\(\widehat{CDE}+\widehat{DCH}=180^0\)

=>\(\widehat{DCH}=180^0-133^0=47^0\)

Ta có: \(\widehat{BCF}+\widehat{BCD}+\widehat{HCD}=180^0\)

=>\(\widehat{BCD}+47^0+68^0=180^0\)

=>\(\widehat{BCD}=65^0\)

a) Để `x/7` là số hữu tỉ thì \(x\in Z\)

b) Để `5/x` là số hữu tỉ thì \(x\in Z,x\ne0\)

c) Để `-5/(2x)` là số hữu tỉ thì \(2x\in Z\Rightarrow x\in Z,x\ne0\)

\(\dfrac{x}{7}\text{ là số hữu tỉ nếu }x\text{ là số nguyên}\)

\(\dfrac{5}{x}\) là số hữu tỉ nếu x là số nguyên khác 0

\(-\dfrac{5}{2x}\)  là số hữu tỉ nếu x là số nguyên khác 0