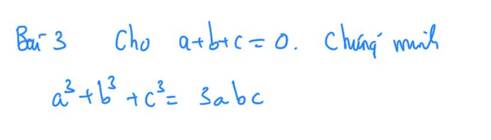Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta xét biểu thức \(P=a^3+b^3+c^3-3abc\) \(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)\(=\left(a+b+c\right)\left[\left(a+b\right)^2-c\left(a+b\right)+c^2\right]-3ab\left(a+b+c\right)\)\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ca-cb+c^2-3ab\right)\)\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\)
Dễ thấy rằng khi \(a+b+c=0\) thì hiển nhiên tích có chứa hạng tử \(a+b+c\) cũng sẽ bằng 0 \(\Rightarrow A=0\) \(\Rightarrow a^3+b^3+c^3-3abc=0\)\(\Rightarrow a^3+b^3+c^3=3abc\)

a) \(\dfrac{2x+1}{3x-2}\) \(=\dfrac{6x-4+5}{3x-2}=2+\dfrac{5}{3x-2}\)nhận giá trị nguyên khi \(\dfrac{5}{3x-2}\) nguyên
<=> 3x-2ϵ{-5;-1;1;5}
Ta có bảng sau;
| 3x-2 | -5 -1 1 5 |
| 3x | -3 1 3 7 |
| x | -1 1/3 (loại) 1 7/3 (loại) |
Vậy để \(\dfrac{2x+1}{3x-2}\)nhận giá trị nguyên khi x=-1;x=1.
tick mình nha
HT

\(a)\) ĐKXĐ: \(a\ne-b;a\ne-c;b\ne-c\)
\(\dfrac{x-ab}{a+b}+\dfrac{x-ac}{a+c}+\dfrac{x-bc}{b+c}=a+b+c\)
\(\Leftrightarrow\left(\dfrac{x-ab}{a+b}-c\right)+\left(\dfrac{x-ac}{a+c}-b\right)+\left(\dfrac{x-bc}{b+c}-a\right)=0\)
\(\Leftrightarrow\dfrac{x-ab-ac-bc}{a+b}+\dfrac{x-ac-ab-bc}{a+c}+\dfrac{x-bc-ab-ac}{b+c}=0\)
\(\Leftrightarrow\left(x-ab-ac-bc\right)\left(\dfrac{1}{a+b}+\dfrac{1}{a+c}+\dfrac{1}{b+c}\right)=0\)
Vì \(a,b,c>0\Rightarrow\dfrac{1}{a+b}+\dfrac{1}{a+c}+\dfrac{1}{b+c}>0\)
\(\Leftrightarrow x-ab-ac-bc=0\)
\(\Leftrightarrow x=ab+ac+bc\)

À (hk2) tbm toán 7.9, tb cả năm thì 8.0 . Vậy kì 2 có được hsg ko ạ!!
học lực kì 2 lấy điểm tb môn kì 2 thôi nhé, nhưng do cháu tb cả năm toán trên 8 nên cả năm vẫn được học sinh giỏi với điều kiện, TB tất cả các môn cả năm trên 8 và Tb toán văn anh không được dưới 6.5 nhé

Đặt \(y+z=p\)
Khi đó \(M=\left(x+p\right)^3+\left(x-p\right)^3\)\(=x^3+3x^2p+3xp^2+p^3+x^3-3x^2p+3xp^2-p^3\)\(=2x^3+6xp^2=2x^3+6x\left(y+z\right)^2=N\) (vì \(y+z=p\))
Từ đó ta có đpcm.

C1 : x3+y3+3xy=(x+y)(x2-xy+y2)+3xy=x2+y2+2xy=(x+y)2=1
C2 : x3+y3+3xy=x3+y3+3xy(x+y)-3xy(x+y)+3xy
=(x+y)3+3xy[1-(x+y)]=1+3xy(1-1)=1+0=1
Mình mới nghĩ ra 2 cách đó thôi à :v

Lời giải:
Áp dụng BĐT Cô-si:
$\frac{1}{x+1}+\frac{x+1}{4}\geq 1$
$\frac{1}{y+1}+\frac{y+1}{4}\geq 1$
$\frac{1}{1+z}+\frac{1+z}{4}\geq 1$
Cộng theo vế:
$A+\frac{x+y+z+3}{4}\geq 3$
$\Rightarrow A\geq 3-\frac{x+y+z+3}{4}\geq 3-\frac{3+3}{4}=\frac{3}{2}$
Vậy $A_{\min}=\frac{3}{2}$ khi $x=y=z=1$
Dự đoán điểm rơi \(x=y=z=1\)
Khi đó \(\dfrac{1}{1+x}=\dfrac{1}{1+1}=\dfrac{1}{2}\) và \(1+x=1+1=2\)
Ta cần ghép Cô-si \(\dfrac{1}{1+x}\) với \(k\left(1+x\right)\) sao cho đảm bảo đấu "=" xảy ra khi \(x=1\)
Đồng thời khi Cô-si 2 số dương trên thì dấu "=" xảy ra khi \(\dfrac{1}{1+x}=k\left(1+x\right)\Leftrightarrow\dfrac{1}{2}=k.2\Leftrightarrow k=\dfrac{1}{4}\)
Như vậy, áp dụng BĐT Cô-si cho 2 số dương \(\dfrac{1}{1+x}\) và \(\dfrac{1+x}{4}\), ta có \(\dfrac{1}{1+x}+\dfrac{1+x}{4}\ge2\sqrt{\dfrac{1}{1+x}.\dfrac{1+x}{4}}=1\)
Tương tự, ta có \(\dfrac{1}{1+y}+\dfrac{1+y}{4}\ge1\) và \(\dfrac{1}{1+z}+\dfrac{1+z}{4}\ge1\)
Cộng vế theo vế của các BĐT vừa tìm được, ta có \(A+\dfrac{x+y+z+3}{4}\ge3\)\(\Leftrightarrow A\ge3-\dfrac{x+y+z+3}{4}\)
Lại có \(x+y+z\le3\) nên \(A\ge3-\dfrac{x+y+z+3}{4}\Leftrightarrow A\ge3-\dfrac{3+3}{4}=\dfrac{3}{2}\)
Vậy GTNN của A là \(\dfrac{3}{2}\) khi \(x=y=z=1\)