Bài 4. (2 điểm): Cho hình vẽ
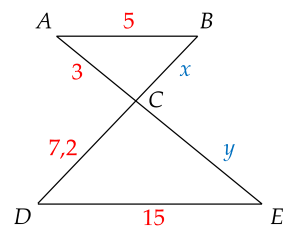
Tính độ dài $x$, $y$ biết $AB$ // $DE$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


=> (x+1) . 5 = (2x + 5) . 3
5x + 5 = 6x + 15
5x + 6x = 15-5
11x =10
x = 11\10

câu a
\(\left(\dfrac{2x}{3x+1}-1\right):\left(1-\dfrac{8x^2}{9x^2-1}\right)\\ =\left(\dfrac{2x}{3x+1}-\dfrac{3x+1}{3x+1}\right):\left(\dfrac{9x^2-1}{9x^2-1}-\dfrac{8x^2}{9x^2-1}\right)\\ =\left(\dfrac{2x}{3x+1}-\dfrac{3x+1}{3x+1}\right):\left(\dfrac{9x^2-1}{\left(3x-1\right)\left(3x+1\right)}-\dfrac{8x^2}{\left(3x-1\right)\left(3x+1\right)}\right)\\ =\left(\dfrac{2x-3x-1}{3x+1}\right):\left(\dfrac{9x^2-1-8x^2}{\left(3x-1\right)\left(3x+1\right)}\right)\)
\(=\left(\dfrac{-x-1}{3x+1}\right):\left(\dfrac{x^2-1}{\left(3x-1\right)\left(3x+1\right)}\right)\\ =\dfrac{-x-1}{3x+1}\cdot\dfrac{\left(3x-1\right)\left(3x+1\right)}{x^2-1}\)
\(=\dfrac{-\left(x+1\right)\cdot\left(3x-1\right)\cdot\left(3x+1\right)}{\left(3x+1\right)\cdot\left(x-1\right)\cdot\left(x+1\right)}\\ =\dfrac{-3x+1}{x-1}\)
câu b
thay \(x=2\) vào P ta được
\(\dfrac{-3\cdot2+1}{2-1}=\dfrac{-6+1}{1}=-5\)
vậy \(P=5\) khi \(x=2\)

câu a)
\(\dfrac{2y-1}{y}-\dfrac{2x+1}{x}\\ =\dfrac{2xy-x}{xy}-\dfrac{2xy+y}{xy}\\ =\dfrac{2xy-x-2xy-y}{xy}\\ =\dfrac{-x-y}{xy}\)
câu b)
\(\dfrac{2x}{3}:\dfrac{5}{6x^2}\\ =\dfrac{2x}{3}\cdot\dfrac{6x^2}{5}\\ =\dfrac{2x\cdot6x^2}{3\cdot5}\\ =\dfrac{12x^3}{15}=\dfrac{4x^3}{5}\)

Giả sử \(r+\sqrt{a}\) là một số hữu tỉ. Đặt \(r+\sqrt{a}=\dfrac{p}{q}\) với \(p,q\inℤ\), \(q\ne0\) và \(\left(p,q\right)=1\).
\(\Leftrightarrow r=\dfrac{p}{q}-\sqrt{a}\)
Vì \(r^3-2ar+1=0\)
\(\Leftrightarrow\left(\dfrac{p}{q}-\sqrt{a}\right)^3-2a.\left(\dfrac{p}{q}-\sqrt{a}\right)+1=0\)
\(\Leftrightarrow\dfrac{p^3}{q^3}-\dfrac{3p^2\sqrt{a}}{q^2}+\dfrac{3ap}{q}-a\sqrt{a}-\dfrac{2ap}{q}+2a\sqrt{a}+1=0\)
\(\Leftrightarrow\dfrac{p^3}{q^3}-\dfrac{3p^2\sqrt{a}}{q^2}+\dfrac{ap}{q}+a\sqrt{a}+1=0\)
\(\Leftrightarrow\dfrac{p^3+apq^2+q^3}{q^3}+\left(\dfrac{aq^2-3p^2}{q^2}\right)\sqrt{a}=0\)
Vì \(p,q,a\inℤ\) nên \(\dfrac{p^3+apq^2+q^3}{q^3}\) và \(\dfrac{aq^2-3p^2}{q^2}\) là các số hữu tỉ. Hơn thế nữa, 0 cũng là một số hữu tỉ, trong khi đó \(\sqrt{a}\) lại là số vô tỉ (vì \(a\) là số nguyên dương không chính phương) nên \(\dfrac{aq^2-3p^2}{q^2}=0\)
\(\Leftrightarrow aq^2=3p^2\)
Nếu \(3⋮a\Rightarrow a\in\left\{1,3\right\}\). Với \(a=1\) thì \(q^2=3p^2\) \(\Rightarrow q⋮3\) \(\Rightarrow q=3k\left(k\inℤ\right)\)
\(\Rightarrow9k^2=3p^2\) \(\Rightarrow p^2=3k^2\) \(\Rightarrow p⋮3\). Từ đây ta có \(p,q⋮3\) , mẫu thuẫn với điều kiện \(\left(p,q\right)=1\)
Với \(a=3\) thì \(q^2=p^2\) \(\Leftrightarrow q=\pm p\) \(\Leftrightarrow r+\sqrt{3}=\pm1\) hay \(r=-\sqrt{3}\pm1\)
Trong trường hợp này, ta thấy \(r^3-2ar+1=\left(-\sqrt{3}\pm1\right)^3-6\left(-\sqrt{3}\pm1\right)+1\ne0\) nên \(a=3\) không thỏa mãn.
Vậy \(3⋮̸a\) \(\Rightarrow p⋮a\) \(\Rightarrow p=al\left(l\inℤ\right)\)
\(\Rightarrow aq^2=3\left(al\right)^2\)
\(\Leftrightarrow q^2=3al^2\)
\(\Rightarrow q⋮a\)
Vậy \(p,q⋮a\). Do \(a>1\) nên từ đây, ta thấy mâu thuẫn với điều kiện \(\left(p,q\right)=1\).
Do đó, điều giả sử là sai \(\Rightarrow r+\sqrt{a}\in I\)
Ở chỗ cuối mình xét thiếu. Từ pt \(aq^2=3p^2\), nếu \(a=3t\) mà \(t\) không phải là SCP thì có \(tq^2=p^2\) \(\Rightarrow p⋮t\) \(\Rightarrow p=tu\) \(\Rightarrow tq^2=t^2u^2\) \(\Rightarrow q^2=tu^2\) \(\Rightarrow q⋮t\) \(\Rightarrow p,q⋮t\), mâu thuẫn.
Còn nếu \(a=3c^2\left(c\ge2\right)\) thì \(p^2=c^2q^2\) \(\Leftrightarrow p=\pm cq\) \(\Leftrightarrow\dfrac{p}{q}=\pm c\)
Lại có \(r=\dfrac{p}{q}-\sqrt{a}=-c\sqrt{3}\pm c\)
Nếu \(r=-c\sqrt{3}+c\) thì \(r^3-2ar+1=\left(-c\sqrt{3}+c\right)^3-6\left(-c\sqrt{3}+c\right)+1\) \(=4c^3+1>0\) với \(c\ge2\), vô lí.
Nếu \(r=-c\sqrt{3}-c\) thì
\(r^3-2ar+1=-4c^3+1< 0\) với \(c\ge2\), vô lí.
Giờ ta mới xét đủ trường hợp để chứng minh giả sử sai.


Cx k khó lắm vẽ hình chứ bn tự làm đc nhỉ:)) mình làm câu a vs B th nha mấy câu kia vẽ rắc rối lắm lười vẽ=))
Bài Làm
a) Áp dụng quan hệ giữa cạnh và đường cao trong tam giác vuông vào tam giác AHC vuông tại H ( H vuông góc BC ) :
\(\Rightarrow\) AH2= AE.AC ( đpcm ) (1)
Áp dụng quan hệ giữa cạnh và đường cao trong tam giác vuông vào tam giác AHB vuông tại H ( H vuông góc BC ) :
\(\Rightarrow\)AH2=AD.AB ( đpcm ) ( 2 )
b) Từ (1) và (2) ta có : AE.AC = AD.AB
\(\Rightarrow\)\(\dfrac{AE}{AD}\)=\(\dfrac{AC}{AB}\)
Xét tam giác ADE và tam giác ABC ta có :
góc A chung
\(\dfrac{AE}{AD}\)=\(\dfrac{AC}{AB}\) (cmt)
\(\Rightarrow\)tam giác ADE đồng dạng với tam giác ABC ( đpcm )

Đặt \(p^n+8=k^3\left(k\inℕ,k\ge3\right)\)
\(\Leftrightarrow k^3-8=p^n\)
\(\Leftrightarrow\left(k-2\right)\left(k^2+2k+4\right)=p^n\)
\(\Leftrightarrow k-2=p^i\left(i\inℕ,i\le n\right)\)
\(\Leftrightarrow k=p^i+2\)
Ta có \(p^n+8=k^3\)
\(\Leftrightarrow p^n+8=\left(p^i+2\right)^3\)
\(\Leftrightarrow p^n=p^{3i}+6p^{2i}+12p^i\) (*)
Đặt \(p^j=\dfrac{p^n}{p^i}\left(j\inℕ,j\le n\right)\), khi đó (*) thành
\(p^j=p^{2i}+6p^{2i}+12\) (**)
Xét \(i=0\Leftrightarrow p^j=19\Leftrightarrow\left(p,j\right)=\left(19,1\right)\) \(\Rightarrow n=1\)
Ta tìm được một bộ \(\left(p,n\right)=\left(17,1\right)\)
Nếu \(j=0\) thì vô lí. Xét \(i,j\ge1\) . Khi đó ta có \(12⋮p\) \(\Rightarrow p\in\left\{2,3\right\}\)
Với \(p=2\), ta có \(2^n+8=k^3\) \(\Rightarrow k⋮2\Rightarrow k=2l\left(l\inℕ\right)\)
\(\Rightarrow2^n+8=8l^3\Leftrightarrow2^{n-3}+1=l^3\) \(\left(n\ge3\right)\)
\(\Leftrightarrow\left(l-1\right)\left(l^2+l+1\right)=2^{n-3}\)
\(\Leftrightarrow l-1=2^m\left(m\le n-3\right)\)
\(\Leftrightarrow l=2^m+1\)
Do đó \(2^{n-3}+1=\left(2^m+1\right)^3\)
\(\Leftrightarrow2^{n-3}=2^{3m}+3.2^{2m}+3.2^m\)
\(\Leftrightarrow2^{n-3-m}=2^{2m}+3.2^m+3\)
\(\Rightarrow3⋮2^{n-3-m}\) \(\Leftrightarrow n-3-m=0\) \(\Leftrightarrow m=n-3\)
\(\Leftrightarrow l^2+l+1=1\) \(\Leftrightarrow l=0\) \(\Leftrightarrow k=0\), vô lí.
Với \(p=3\), ta có \(3^n+8=k^3\) \(\Rightarrow k\) chia 3 dư 2 \(\Rightarrow k=3q+2\left(q\inℕ^∗\right)\)
\(\Rightarrow3^n+8=\left(3q+2\right)^3\)
\(\Leftrightarrow3^n=27q^3+54q^2+36q\)
\(\Leftrightarrow3^{n-2}=q\left(3q^2+6q+4\right)\) \(\left(n\ge2\right)\)
Dễ thấy nếu \(n=2\) thì vô lí. Xét \(n\ge3\). Khi đó vì \(3q^2+6q+4⋮̸3\) nên \(3q^2+6q+4=1\), vô lí.
Vậy \(\left(p,n\right)=\left(19,1\right)\) là cặp số duy nhất thỏa mãn ycbt.

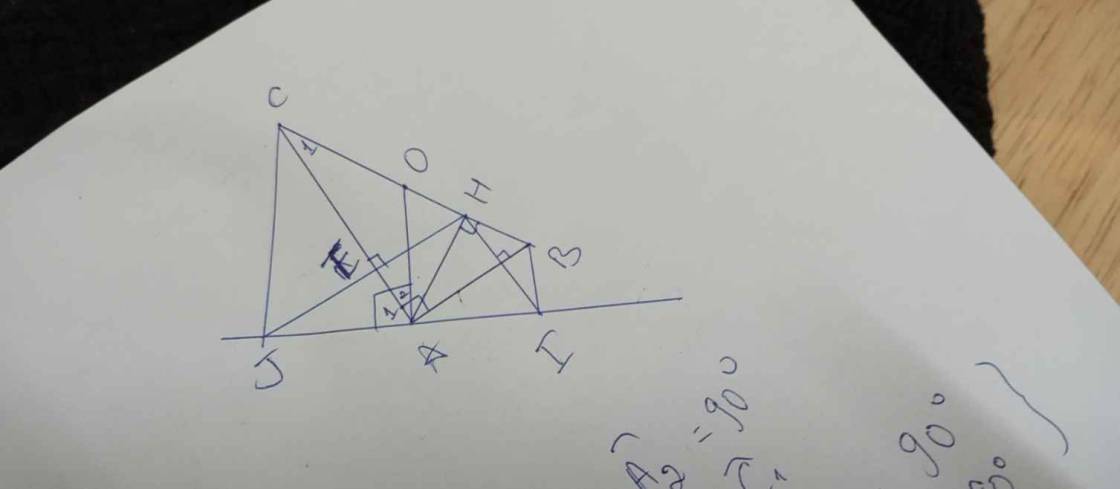
Câu e:
$\widehat {A_1}+\widehat{A_2}=90^{\circ}$
$\widehat{A_2}=\widehat{C_1}$
$\Rightarrow \widehat{A_1}+\widehat{C_1}=90^{\circ}$
Mặt khác $\widehat{C_1}+\widehat{CAH} = 90^{\circ}$
Suy ra $A_1=\widehat{CAH}$ (1)
Chứng minh được $\Delta JAE = \Delta HAE$ (cgv-gn)
$\Rightarrow AJ=AH$ (2)
Từ (1); (2) và chung cạnh $AC$ ta suy ra $\Delta AJC=\Delta AHC$ (c.g.c).
Suy ra $\widehat {J}=90^{\circ}$ hay $CJ\bot IJ$.
Chứng minh tương tự $BI \bot IJ$.
Do AB // DE (gt)
Theo hệ quả của định lý Thalès, ta có:
AB/DE = BC/CD
x = BC = AB.CD : DE
x = BC = 5.7,2 : 15 = 2,4
Do AB // DE (gt)
Theo hệ quả của định lý Thalès, ta có:
AB/DE = AC/CE
y = CE = AC.DE : AB
= 3.15 : 7,2
= 6,25