\(4-2\sqrt{3}\) \(+2\sqrt{3}+1\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(\sqrt{14}-3\sqrt{2}\right)^3+6\sqrt{28}\)
\(=\left(\sqrt{14}\right)^2-2\cdot3\sqrt{2}\cdot\sqrt{14}+\left(3\sqrt{2}\right)^2+6\cdot2\sqrt{7}\)
\(=14-6\sqrt{28}+9\cdot2+12\sqrt{7}\)
\(=14-6\cdot2\sqrt{7}+18+12\sqrt{7}\)
\(=\left(14+18\right)+\left(12\sqrt{7}-12\sqrt{7}\right)\)
\(=32\)

ĐKXĐ: m 1
a) Thay tọa độ điểm A(1; 2) vào hàm số, ta được:
(m - 1).1 + 1 = 2
m - 1 + 1 = 2
m = 2 (nhận)
Vậy m = 2 thì đồ thị của hàm số đi qua điểm A(1; 2)
b) Thay tọa độ điểm B(3; -2) vào hàm số ta được:
(m - 1).3 + 1 = -2
3m - 3 + 1 = -2
3m - 2 = -2
3m = 0
m = 0 (nhận)
Vậy m = 0 thì đồ thị của hàm số đi qua điểm B(3; -2)
c) Với m = 2 y = x + 1
Với m = 0 y = -x + 1
*) Đồ thị
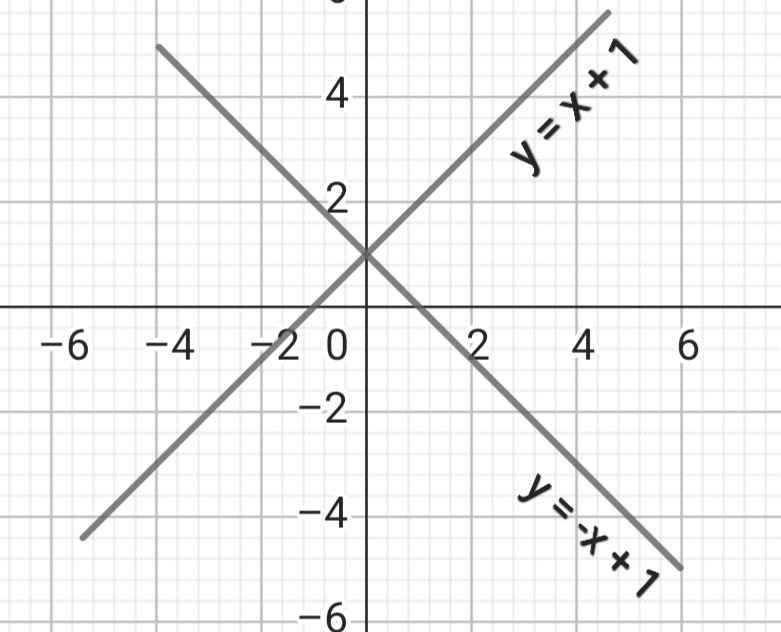

Bạn nên tách lẻ từng bài ra từng post để mọi người dễ dàng hỗ trợ hơn nhé.

gọi Vận tốc ban đầu của ô tô là: x (km/h) (x E N*)
Ta có : thời gian ô tô đi lần đầu là : \(\dfrac{250}{x}\)( h ).
Vận tốc lúc về là : x+10(km/h).
Thời gian lúc về là: \(\dfrac{250-10}{x+10}\)=\(\dfrac{240}{x+10}\) ( h ).
Ta có: thời gian lúc đi: \(\dfrac{250}{x}\)=\(\dfrac{240}{x+10}\)+1 ( h).
giải phương trình ta được: x=50(km/h).
Vậy . . .

Gọi số cá năm ngoái nhà bác Hải thu được là x
Gọi số cá năm ngoái nhà bác Dương thu được là y
Ta có hệ PT
\(\left\{{}\begin{matrix}x+y=75\\120\%.x+118\%.y=89,2\end{matrix}\right.\)
Giải hệ để tìm x; y

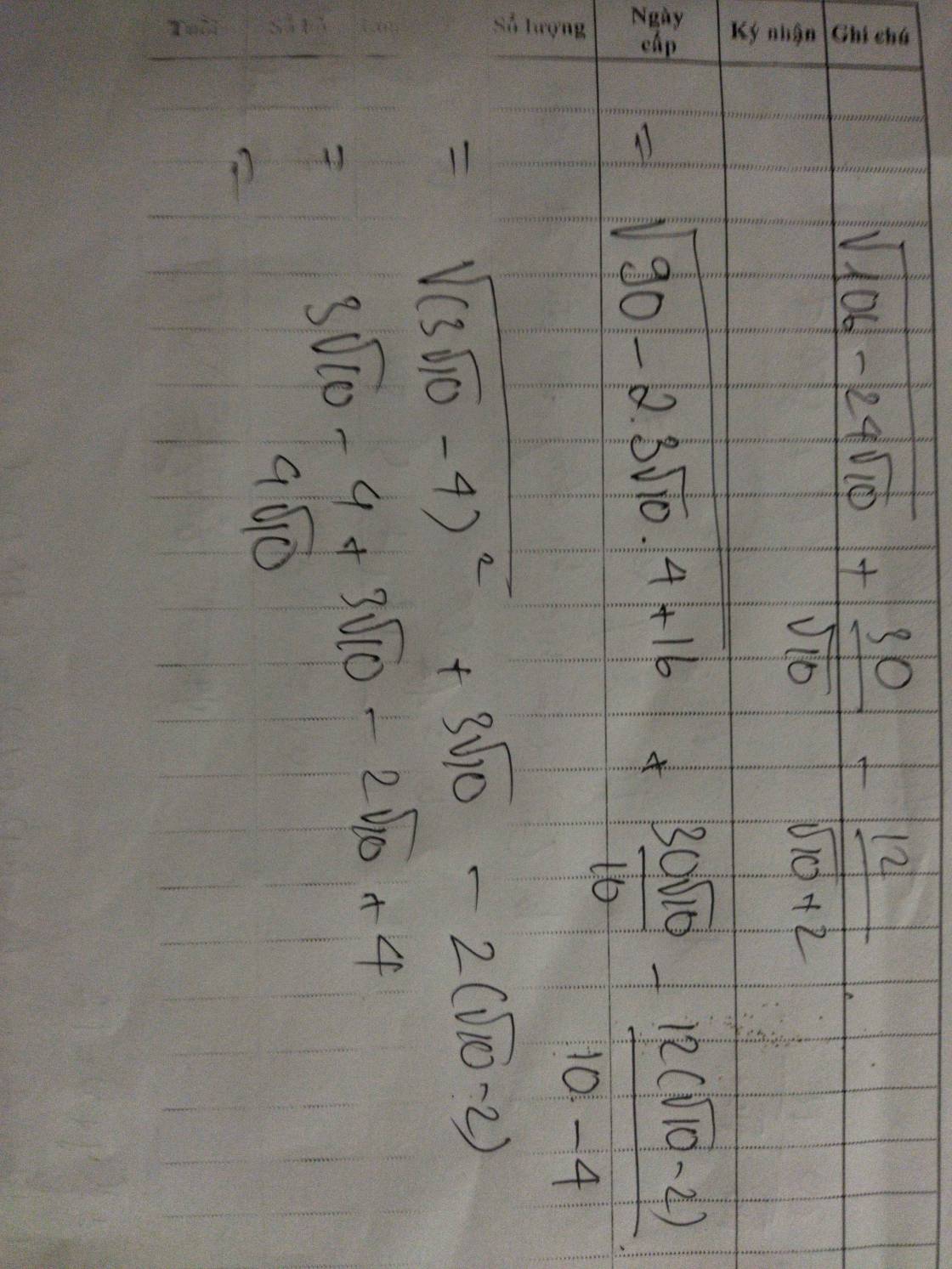
Lời giải:
\(=\sqrt{106-2\sqrt{1440}}+3\sqrt{10}-\frac{12(\sqrt{10}-2)}{(\sqrt{10}+2)(\sqrt{10}-2)}\)
\(=\sqrt{(\sqrt{90}-\sqrt{16})^2}+3\sqrt{10}-\frac{12(\sqrt{10}-2)}{6}\)
$=\sqrt{90}-\sqrt{16}+3\sqrt{10}-2(\sqrt{10}-2)$
$=4\sqrt{10}$

Để chứng minh rằng biểu thức 34n+1 + 2.32n+2 - 21 chia hết cho 64, ta cần sử dụng phương pháp toán học gọi là "chứng minh bằng quy nạp". Bước 1: Kiểm tra điều kiện ban đầu - Khi n = 0, ta có: - Biểu thức ban đầu = 34(0) + 1 + 2.32(0) +2 -21 = -20. - Vì -20 không chia hết cho số nguyên dương nào khác của số nguyên tố lớn nhất trong các số nguyên tố nhỏ hơn hoặc bằng căn bậc hai của số này (tức là căn bậc hai của |64|), nên không thể kết luận rằng biểu thức trên chia hết cho 64. Bước 2: Giả sử giả thiết quy nạp - Giả sử với một giá trị nguyên dương k (k ≥0), biểu thức sau: P(k):=34k+1 +2.32k+2-21 Chia hết cho số nguyên tố lớn nhất trong các số nguyên tố nhỏ hơn hoặc bằng căn bậc hai của |64|. Bước 3: Chứng minh công thức quy nạp - Ta cần chứng minh rằng nếu P(k) chia hết cho 64, thì P(k+1) cũng chia hết cho 64. - Giả sử P(k) chia hết cho 64, tức là tồn tại một số nguyên dương a sao cho: P(k) = 64a. - Ta cần chứng minh rằng tồn tại một số nguyên dương b sao cho: P(k+1) = 34(k+1)+1 +2.32(k+1)+2 -21 = 34k +35 +2.32k +36 -21 = (34k+1 +2.32k+2 -21) + (34*34 + 2*32*36). Vì biểu thức trong ngoặc đơn là giá trị cố định không phụ thuộc vào k, ta có thể viết lại biểu thức trên thành: P(k+1) = (P(k)) + C, trong đó C là một giá trị cố định không phụ thuộc vào k. - Như vậy, ta có: P(k+1) = (P(K)) + C = (64a) + C. - Với a và C là các số nguyên dương, ta có thể viết lại biểu thức trên thành: P(K+1)=b * |64|, trong đó b=a+C. Bước 4: Kết luận Vì đã xác nhận rằng nếu P(k) chia hết cho 64 thì P(k+1) cũng chia hết cho 64, và với giá trị ban đầu n=0, biểu thức không chia hết cho 64, ta có thể kết luận rằng biểu thức 34n+1 +2.32n+2 -21 không chia hết cho 64 với mọi số nguyên dương n.
đúng hay sai e không biết em làm trên chat gpt


ff đi mày