noi phet quen doi 

bạn rảnh quá nhỉ

=13415643216848756423155511112

bạn tính thử đi :))

tớ gửi lời mời rồi nha

:))

323 nhé

323 rùi

o biet

khó thế không biết

a) Nối C đến D.

Ta có 2 đường tròn bằng nhau => AC = AD

=> ∆ ACD cân tại A

Lại có góc ABC = 90°; do có OB = OC = OA = R ( tính chất trung tuyến ứng với cạnh huyền )

Tương tự có góc ABD = 90°

=> ABC + ABD = 180°

=> C; B; D thẳng hàng và AB ⊥ CD

=> BC = BD

=> cung BC = cung BD

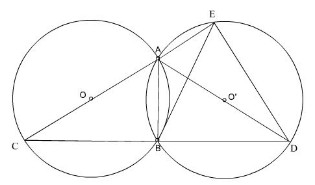
b) Nối E đến D; từ B hạ BH ⊥ ED Ta có góc DEA = 90° ( chứng minh tương tự theo (a) )

=> BH // EC

Mà theo (a) ta có BE = BD

=> BH là đường trung bình tam giác CDE

=> HE = HD mà BH ⊥ ED => B là điểm chính giữa cung EBD

a) Nối C đến D.

Ta có 2 đường tròn bằng nhau => AC = AD

=> ∆ ACD cân tại A

Lại có góc ABC = 90°; do có OB = OC = OA = R ( tính chất trung tuyến ứng với cạnh huyền )

Tương tự có góc ABD = 90°

=> ABC + ABD = 180°

=> C; B; D thẳng hàng và AB ⊥ CD

=> BC = BD

=> cung BC = cung BD

b) Nối E đến D; từ B hạ BH ⊥ ED Ta có góc DEA = 90° ( chứng minh tương tự theo (a) )

=> BH // EC

Mà theo (a) ta có BE = BD

=> BH là đường trung bình tam giác CDE

=> HE = HD mà BH ⊥ ED => B là điểm chính giữa cung EBD

O A B C D K

Kẽ OA cắt đường tròn tại D cắt BC tại K

Ta có OA = OB = OD = R

\(\Rightarrow\)\(\Delta ABD\) vuông tại D

\(\Rightarrow BD=\sqrt{OD^2-AB^2}=\sqrt{10^2-8^2}=6\)

Ta có OK là đường trung trực của BC nên \(\hept{\begin{cases}OK⊥BC\\BK=CK\end{cases}}\)

Ta lại có: \(S_{\Delta ABD}=\frac{1}{2}AB.BD=\frac{1}{2}AD.BK\)

\(\Rightarrow BK=\frac{AB.BD}{AD}=\frac{8.6}{10}=4,8\)

\(\Rightarrow BC=2BK=4,8.2=9,6\)

Viết nhầm tùm lum hết. Do không thấy cái hình. Mà thôi nhìn hình sửa hộ luôn  nhé

Đễ thấy \(x=y=z=0\) là 1 nghiệm của hệ

Xét \(\hept{\begin{cases}x\ne0\\y\ne0\\z\ne0\end{cases}}\)

Cộng 3 phương trình vế theo vế ta được

\(\frac{2x^2}{x^2+1}+\frac{2y^2}{y^2+1}+\frac{2z^2}{z^2+1}=x+y+z\)

Ta có: \(\frac{2x^2}{x^2+1}\le\frac{2x^2}{2x}=x\)

Tương tự: \(\hept{\begin{cases}\frac{2y^2}{y^2+1}\le y\\\frac{2z^2}{z^2+1}\le z\end{cases}}\)

Cộng vế theo vế ta được:

\(\frac{2x^2}{x^2+1}+\frac{2y^2}{y^2+1}+\frac{2z^2}{z^2+1}\le x+y+z\)

Dấu =  xảy ra khi \(x=y=z=1\)

Vậy nghiệm của hệ là: \(\left(x,y,z\right)=\left(0,0,0;1,1,1\right)\)

PS: Tính không làm đâu nhưng mà đồng hương nên giúp nhau vậy :D

nhìn hpt bự con thế này chắc xài BĐT giải r`, chờ mình tẹo :)