một cửa hàng có 9 540kg đường. buổi sáng cửa hàng bán được 3 170kg đường, buổi chiều bán được 1 324kg đường. hỏi sau hai lần bán cửa hàng còn lại bao nhiêu ki-lô-gam đường?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nữa quãng đường từ nhà đến chợ là:
\(3880:2=1940\left(m\right)\)
Gấp 3 lần từ nhà đến công ty là:
\(1940+260=2200\left(m\right)\)
Quãng đường từ nhà đến công ty là:
\(2200:3=\dfrac{2200}{3}\left(m\right)\)
Đáp số: ...

Bài 8:
a)\(2x-\dfrac{3}{5}=\dfrac{28}{15}\cdot\dfrac{6}{35}\)
\(\Rightarrow2x-\dfrac{3}{5}=\dfrac{8}{25}\)
\(\Rightarrow2x=\dfrac{8}{25}+\dfrac{3}{5}\)
\(\Rightarrow2x=\dfrac{23}{25}\)
\(\Rightarrow x=\dfrac{23}{25}:2=\dfrac{23}{50}\)
b) \(\dfrac{8}{23}\cdot\dfrac{46}{24}-x=\dfrac{1}{3}\)
\(\Rightarrow\dfrac{2}{3}-x=\dfrac{1}{3}\)
\(\Rightarrow x=\dfrac{2}{3}-\dfrac{1}{3}\)
\(\Rightarrow x=\dfrac{1}{3}\)
c) \(\dfrac{3}{22}-\dfrac{3}{4}x=\dfrac{27}{121}\cdot\dfrac{11}{9}\)
\(\Rightarrow\dfrac{3}{22}-\dfrac{3}{4}x=\dfrac{3}{11}\)
\(\Rightarrow\dfrac{3}{4}x=\dfrac{3}{22}-\dfrac{3}{11}\)
\(\Rightarrow\dfrac{3}{4}x=-\dfrac{3}{22}\)
\(\Rightarrow x=\dfrac{-3}{22}:\dfrac{3}{4}=-\dfrac{2}{11}\)
d) \(1-\dfrac{2}{3}x=\dfrac{49}{15}\cdot\dfrac{5}{7}\)
\(\Rightarrow1-\dfrac{2}{3}x=\dfrac{7}{3}\)
\(\Rightarrow\dfrac{2}{3}x=1-\dfrac{7}{3}\)
\(\Rightarrow\dfrac{2}{3}x=\dfrac{-4}{3}\)
\(\Rightarrow x=\dfrac{-4}{3}:\dfrac{2}{3}=-2\)

Vì abc là số có 3 chữ số và abc = (a+b+c)3
=> 99 < abc <1000
=> 13 < (a+b+c)3 < 103
=> 1 < (a+b+c) < 10
+) Nếu a+b+c = 9
Ta có: abc = (a+b+c)3 = 93 = 729
mà a+b+c = 7+2+9 = 18 ≠≠9 (loại)
+) Nếu a+b+c = 8
Ta có abc = (a+b+c)3 = 83 = 512
mà a+b+c = 5+1+2 = 8 (đúng)
Vậy abc = 512
tick cho mik nhé, làm ơn

Ta có:
`255/272 = (15 ×17)/(16×17) = 15/16`
Phân số này vẫn có thể rút gọn nên không phải phân số tối giản

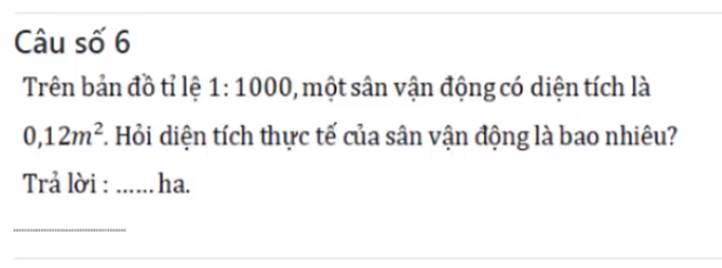
Diện tích thực tế của sân vận động đó là:
0,12x1000=120 (m2)
Đổi : 120 m2=0,012 ha
Đáp số: 0,012 ha

A B C E F H M K D I
a/
E và F bình đẳng nhau nên tôi chỉ c/m ME là tiếp tuyến với đường tròn đường kính AH. Còn c/m MF là tiếp tuyến làm tương tự bạn tự c/m nhé
Gọi I là tâm đường tròng đường kính AH => IA=IH
Gọi D là giao của AH với BC
Xét tg ABC có \(AH\perp BC\) (trong tg 3 đường cao đồng quy)
\(\Rightarrow AD\perp BC\)
Xét tg vuông ADC và tg vuông BEC có
\(\widehat{DAC}=\widehat{EBC}\) (cùng phụ với \(\widehat{C}\) ) (1)
Xét tg vuông AHE có
\(IA=IH\Rightarrow IE=IA=IH=\dfrac{AH}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
\(\Rightarrow E\in\left(I\right)\) và tg AIE cân tại I
\(\Rightarrow\widehat{DAC}=\widehat{AEI}\) (góc ở đáy tg cân) (2)
Xét tg vuông BEC có
\(MB=MC\left(gt\right)\Rightarrow ME=MB=MC=\dfrac{BC}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
=> tg BME cân tại M
\(\Rightarrow\widehat{EBC}=\widehat{BEM}\) (góc ở đáy tg cân) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{AEI}=\widehat{BEM}\)
Mà \(\widehat{AEI}+\widehat{BEI}=\widehat{AEB}=90^o\)
\(\Rightarrow\widehat{BEM}+\widehat{BEI}=\widehat{MEI}=90^o\Rightarrow ME\perp IE\) => ME là tiếp tuyến với đường tròn đường kính AH
b/
Xét tg MEK và tg MAE có
\(\widehat{AME}\) chung
Ta có
\(sđ\widehat{MEK}=\dfrac{1}{2}sđcungEK\) (góc giữa tiếp tuyến và dây cung)
\(sđ\widehat{MAE}=\dfrac{1}{2}sđcungEK\) (góc nội tiếp (O))
\(\Rightarrow\widehat{MEK}=\widehat{MAE}\)
=> tg MEK đồng dạng với tg MAE (g.g.g)
\(\Rightarrow\dfrac{ME}{MA}=\dfrac{MK}{ME}\Rightarrow MK.MA=ME^2\)

\(B=3x^2+3y^2+z^2+5xy-3yz-3xz-2x-2y+3\\\Rightarrow4A=12x^2+12y^2+4z^2+20xy-12yz-12xz-8x-8y+12\\\\=[(9x^2+18xy+9y^2)-(12xz+12yz)+4z^2]+[(2x^2+4xy+2y^2)-(8x+8y)+8]+(x^2-2xy+y^2)+4\\=[(3x+3y)^2-2\cdot(3x+3y)\cdot2z+(2z)^2]+[2(x^2+2xy+y^2)-8(x+y)+8]+(x-y)^2+4\\=(3x+3y-2z)^2+2[(x+y)^2-4(x+y)+4]+(x-y)^2+4\\=(3x+3y-2z)^2+2(x+y-2)^2+(x-y)^2+4\)
Ta thấy: \(\left\{{}\begin{matrix}\left(3x+3y-2z\right)^2\ge0\forall x,y,z\\2\left(x+y-2\right)^2\ge0\forall x,y\\\left(x-y\right)^2\ge0\forall x,y\end{matrix}\right.\)
\(\Rightarrow\left(3x+3y-2z\right)^2+2\left(x+y-2\right)^2+\left(x-y\right)^2+4\ge4\forall x,y,z\)
\(\Leftrightarrow4B\ge4\Leftrightarrow B\ge1\)
Dấu \("="\) xảy ra khi: \(\left\{{}\begin{matrix}3x+3y-2z=0\\x+y-2=0\\x-y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=x\\2x=2\\2z=6x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=y=1\\z=3\end{matrix}\right.\)
Vậy \(Min_B=1\) khi \(x=y=1;z=3\).
\(Toru\)

a: Xét ΔBAC có AM là phân giác
nên \(\dfrac{BM}{MC}=\dfrac{AB}{AC}\)
=>\(\dfrac{BM}{MC}=\dfrac{a}{b}\)
=>\(\dfrac{BM}{a}=\dfrac{MC}{b}\)
mà BM+MC=BC=a
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BM}{a}=\dfrac{MC}{b}=\dfrac{BM+MC}{a+b}=\dfrac{a}{a+b}\)
=>\(BM=\dfrac{a\cdot a}{a+b}=\dfrac{a^2}{a+b}\)
Xét ΔBCA có CN là phân giác
nên \(\dfrac{BN}{NA}=\dfrac{BC}{CA}\)
=>\(\dfrac{BN}{NA}=\dfrac{a}{b}\)
=>\(\dfrac{BN}{NA}=\dfrac{BM}{MC}\)
Xét ΔBAC có \(\dfrac{BN}{NA}=\dfrac{BM}{MC}\)
nên MN//AC
b: Xét ΔBAC có MN//AC
nên \(\dfrac{MN}{AC}=\dfrac{BM}{BC}\)
=>\(\dfrac{MN}{b}=\dfrac{a^2}{a+b}:a=\dfrac{a}{a+b}\)
=>\(MN=\dfrac{a\cdot b}{a+b}\)

a: 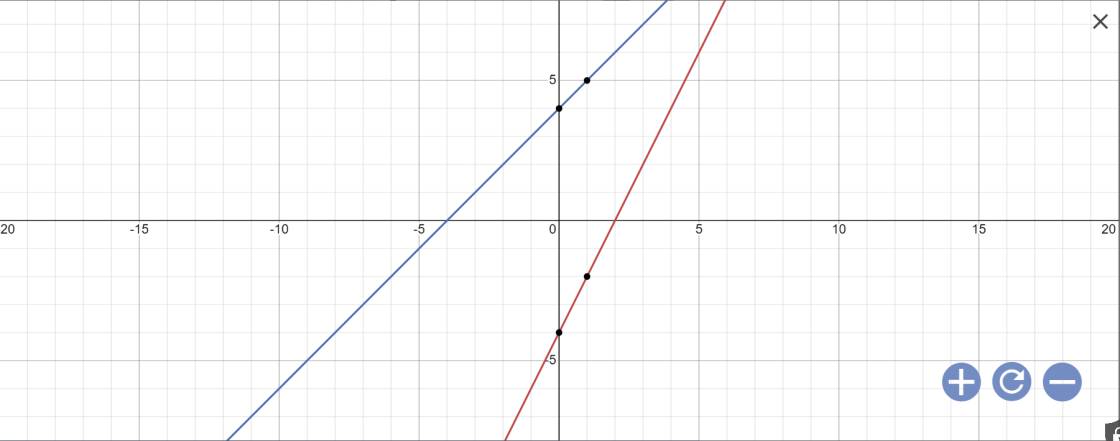
b: Phương trình hoành độ giao điểm là:
2x-4=x+4
=>2x-x=4+4
=>x=8
Thay x=8 vào y=x+4, ta được:
y=8+4=12
Vậy: Q(8;12)
Tọa độ N là:
\(\left\{{}\begin{matrix}x=0\\y=2\cdot0-4=-4\end{matrix}\right.\)
Vậy: N(0;-4)
Tọa độ M là:
\(\left\{{}\begin{matrix}x=0\\y=0+4=4\end{matrix}\right.\)
Vậy: M(0;4)
M(0;4); N(0;-4); Q(8;12)
\(MN=\sqrt{\left(0-0\right)^2+\left(-4-4\right)^2}=8\)
\(MQ=\sqrt{\left(8-0\right)^2+\left(12-4\right)^2}=\sqrt{8^2+8^2}=8\sqrt{2}\)
\(NQ=\sqrt{\left(8-0\right)^2+\left(12+4\right)^2}=\sqrt{8^2+16^2}=8\sqrt{5}\)
Xét ΔMNQ có \(cosMNQ=\dfrac{NM^2+NQ^2-MQ^2}{2\cdot NM\cdot NQ}=\dfrac{256}{2\cdot8\cdot8\sqrt{5}}=\dfrac{2}{\sqrt{5}}\)
=>\(sinMNQ=\sqrt{1-\left(\dfrac{2}{\sqrt{5}}\right)^2}=\dfrac{1}{\sqrt{5}}\)
Diện tích ΔMNQ là:
\(S_{MNQ}=\dfrac{1}{2}\cdot NM\cdot NQ\cdot sinMNQ\)
\(=\dfrac{1}{2}\cdot\dfrac{1}{\sqrt{5}}\cdot8\cdot8\sqrt{5}=\dfrac{64}{2}=32\)
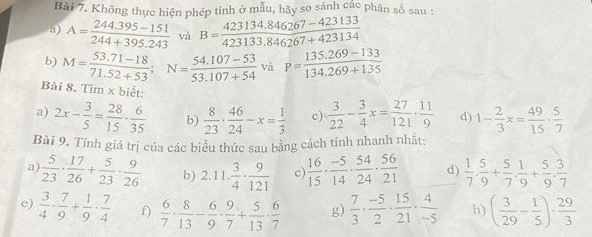

Sau buổi sáng cửa hàng còn lại số kilogam đường là:
\(9540-3170=6370\left(kg\right)\)
Sau hai buổi thì cửa hàng còn số kilogam đường là:
\(6370-1324=5046\left(kg\right)\)
ĐS: ...
Sau buổi sáng cửa hàng còn lại số kilogam đường là:
9540−3170=6370(kg)
Sau hai buổi thì cửa hàng còn số kilogam đường là:
6370−1324=5046(kg)
ĐS: 5046kg