\(\dfrac{4^5\cdot9^4}{8^3\cdot27^3}=\dfrac{\left(2^2\right)^5\cdot\left(3^2\right)^4}{\left(2^3\right)^3\cdot\left(3^3\right)^3}=\dfrac{2^{10}\cdot3^8}{2^9\cdot3^9}=\dfrac{2}{3}\)

\(\dfrac{4^{20}\cdot3^{35}}{2^{37}\cdot27^{12}}=\dfrac{\left(2^2\right)^{20}\cdot3^{35}}{2^{37}\cdot\left(3^3\right)^{12}}=\dfrac{2^{40}\cdot3^{35}}{2^{37}\cdot3^{36}}=\dfrac{2^3}{3}\)

\(\dfrac{5^4\cdot20^4}{25^5\cdot4^5}=\dfrac{5^4\cdot5^4\cdot4^4}{5^5\cdot5^5\cdot4^5}=\dfrac{1}{5^2\cdot4}=\dfrac{1}{100}\)

\(\dfrac{2^{15}\cdot9^4}{6^6\cdot8^3}=\dfrac{2^{15}\cdot\left(3^2\right)^4}{2^6\cdot3^6\cdot\left(2^3\right)^3}=\dfrac{2^{15}\cdot3^8}{2^6\cdot3^6\cdot2^9}=3^2\)

A = 0,(36) - 0,(71)

= 36/99 - 71/99

= -35/99

B = [3,(12) - 2,(5)] : 0,(14)

= (103/33 - 203/99) : 14/99

= 106/99 : 14/99

= 53/7

\(A=0,\left(36\right)-0,\left(71\right)\)

\(A=\dfrac{36}{99}-\dfrac{71}{99}=-\dfrac{35}{99}=-0,\left(35\right)\)

\(B=\left[3,\left(12\right)-2,\left(5\right)\right]:0,\left(14\right)\)

\(B=\left(\dfrac{3\cdot99+12}{99}-\dfrac{2\cdot9+5}{9}\right):\dfrac{14}{99}\)

\(B=\left(\dfrac{309}{99}-\dfrac{23}{9}\right):\dfrac{14}{99}\)

\(B=\dfrac{56}{99}:\dfrac{14}{99}\)

\(B=4\)

\(\dfrac{79}{11}=7+\dfrac{2}{11}=7+\dfrac{18}{99}\)

\(=7,\left(18\right)\)

\(\dfrac{91}{37}=2+\dfrac{17}{37}=2+\dfrac{459}{999}\)

\(=2,\left(459\right)\)

79/11 = 7,(18)

91/37 = 2,(459)

Chuyển đổi cụ thể:

\(\dfrac{79}{11}=\dfrac{79\cdot9}{11\cdot9}=\dfrac{711}{99}=7\dfrac{18}{99}\)

\(=7,\left(18\right)\)

\(\dfrac{79}{11}=7,\left(18\right)\)

\(\dfrac{1}{6}=0,1\left(6\right)\)

\(\dfrac{1}{3}=0,\left(3\right)\)

\(\dfrac{2}{3}=0,\left(6\right)\)

1/6 = 0,1(6)

1/3 = 0,(3)

2/3 = 0,(6)

a)\(\dfrac{27^4.4^3}{9^5.8^2}\)

=\(\dfrac{3^{12}.2^6}{3^{10}.2^6}\)

=3\(^2\)=9

b)\(\dfrac{3^{29}.4^{16}}{27^9.8^{11}}\)

=\(\dfrac{3^{29}.2^{32}}{3^{27}.2^{33}}\)

=\(\dfrac{9}{2}\)

\(\dfrac{27^4.4^3}{9^5.8^2}=\dfrac{\left(3^3\right)^4.\left(2^2\right)^3}{\left(3^2\right)^5.\left(2^3\right)^2}=\dfrac{3^{12}.2^6}{3^{10}.2^6}=\dfrac{3^{12}}{3^{10}}=3^2=9\)

_________

\(\dfrac{3^{29}.4^{16}}{27^9.8^{11}}=\dfrac{3^{29}.\left(2^2\right)^{16}}{\left(3^3\right)^9.\left(2^3\right)^{11}}=\dfrac{3^{29}.2^{32}}{3^{27}.2^{33}}=\dfrac{1}{3^2.2}=\dfrac{1}{9.2}=\dfrac{1}{18}\)

a) Để tính góc zOm, ta biết rằng tia Om là tia phân giác của góc zOy. Vì góc zOy là 60 độ, nên góc zOm cũng là 60/2 = 30 độ.

b) Để xác định xem tia Ox có phải là tia phân giác của góc yOn hay không, ta cần vẽ tia On là tia đối của tia Om. Sau đó, ta kiểm tra xem tia Ox có đi qua điểm phân giác của góc yOn hay không.

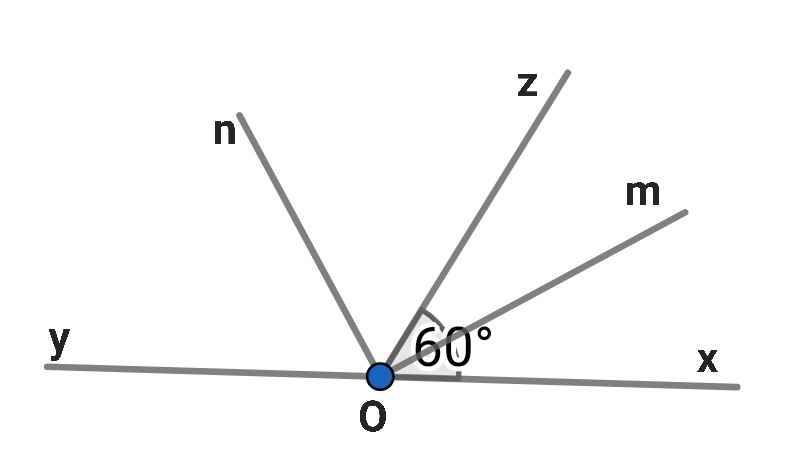 a) Do Om là tia phân giác của ∠xOz 

⇒ ∠xOm = ∠zOm = xOz : 2 = 60⁰ : 2 = 30⁰

b) Ta có:

∠xOz + ∠yOz = 180⁰ (kề bù)

⇒ ∠yOz = 180⁰ - ∠xOz

= 180⁰ - 60⁰

= 120⁰

Do On là tia phân giác của ∠zOy

⇒ ∠yOn = ∠zOn = zOy : 2 = 120⁰ : 2 = 60⁰

c) ∠mOn = ∠mOz + ∠zOn

= 30⁰ + 60⁰

= 90⁰

.

Lời giải:

$(\frac{1}{3})^{2x-1}=\frac{1}{243}=(\frac{1}{3})^5$

$\Rightarrow 2x-1=5$

$\Rightarrow 2x=6$

$\Rightarrow x=3$

      \(\left(\dfrac{1}{3}\right)^{2x-1}=\dfrac{1}{243}\)

      \(\left(\dfrac{1}{3}\right)^{2x-1}=\left(\dfrac{1}{3}\right)^5\)

=> \(2x-1=5\) 

           \(2x=6\) 

             \(x=3\)

\(2\left(x-3\right)+3x+0,5=\dfrac{3}{4}\\ \Leftrightarrow2x-6+3x+\dfrac{1}{2}=\dfrac{3}{4}\\ \Leftrightarrow x\left(2+3\right)=\dfrac{3}{4}-\dfrac{1}{2}+6\\ \Leftrightarrow5x=\dfrac{25}{4}\\ \Leftrightarrow x=\dfrac{25}{4}:5=\dfrac{5}{4}\\ ---\\ 4^{x+2}+4^x=272\\ \Leftrightarrow4^x\left(4^2+1\right)=272\\ \Leftrightarrow4^x.17=272\\ \Leftrightarrow4^x=\dfrac{272}{17}=16=4^2\\ Vậy:x=2\\ ----\\ \left(1,2-5x\right)\left(2\dfrac{1}{8}+\dfrac{1}{2}x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}1,2-5x=0\\2,125+0,5x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}5x=1,2\\0,5x=-2,125\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1,2}{5}=0,24\\x=\dfrac{-2,125}{0,5}=-4,25\end{matrix}\right.\)

a) \(2\left(x-3\right)+3x+0,5=\dfrac{3}{4}\)

\(\Rightarrow2x-6+3x+\dfrac{1}{2}=\dfrac{3}{4}\)

\(\Rightarrow5x-6=\dfrac{3}{4}-\dfrac{1}{2}\)

\(\Rightarrow5x-6=\dfrac{1}{4}\)

\(\Rightarrow5x=\dfrac{1}{4}+6\)

\(\Rightarrow5x=\dfrac{25}{4}\)

\(\Rightarrow x=\dfrac{25}{4}:5\)

\(\Rightarrow x=\dfrac{5}{4}\)

b) \(4^{x+2}+4^x=272\)

\(\Rightarrow4^x\cdot4^2+4^x\cdot1=272\)

\(\Rightarrow4^x\cdot\left(16+1\right)=272\)

\(\Rightarrow4^x\cdot17=272\)

\(\Rightarrow4^x=16\)

\(\Rightarrow4^x=4^2\)

\(\Rightarrow x=2\)

c) \(\left(1,2-5x\right)\left(2\dfrac{1}{8}+\dfrac{1}{2}x\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}1,2-5x=0\\\dfrac{15}{8}+\dfrac{1}{2}x=0\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}5x=1,2\\\dfrac{1}{2}x=-\dfrac{15}{8}\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1,2}{5}\\x=-\dfrac{15}{8}:\dfrac{1}{2}\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{6}{25}\\x=-\dfrac{15}{4}\end{matrix}\right.\)