
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{HBA}\) chung
Do đó: ΔHBA~ΔABC
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)
=>\(BA^2=BH\cdot BC\)
b: Xét ΔABM có
AH là đường cao
AH là đường trung tuyến
Do đó: ΔABM cân tại A
=>\(\widehat{AMB}=\widehat{ABM}\)
mà \(\widehat{AMB}=\widehat{CMK}\)(hai góc đối đỉnh)
nên \(\widehat{ABM}=\widehat{CMK}\)
Xét ΔHBA vuông tại H và ΔKMC vuông tại K có
\(\widehat{HBA}=\widehat{KMC}\)
Do đó: ΔHBA~ΔKMC
d: Gọi N là giao điểm của IM với CA
Xét ΔCAI có
AK,CH là các đường cao
AK cắt CH tại M
Do đó: M là trực tâm của ΔCAI
=>IM\(\perp\)CA tại N
Xét ΔCKA vuông tại K và ΔCNI vuông tại N có
\(\widehat{KCA}\) chung
Do đó: ΔCKA~ΔCNI
=>\(\dfrac{CK}{CN}=\dfrac{CA}{CI}\)
=>\(CK\cdot CI=CA\cdot CN\)
Xét ΔAHC vuông tại H và ΔANI vuông tại N có
\(\widehat{HAC}\) chung
Do đó: ΔAHC~ΔANI
=>\(\dfrac{AH}{AN}=\dfrac{AC}{AI}\)
=>\(AH\cdot AI=AN\cdot AC\)
\(CK\cdot CI+AH\cdot AI\)
\(=AN\cdot AC+CN\cdot AC\)
\(=AC\left(AN+CN\right)=AC^2\)

Gọi độ dài quãng đường AB là x (km) với x>0
Thời gian người đó đi từ A đến B là: \(\dfrac{x}{35}\) giờ
Do lúc về đi con đường khác dài hơn đường cũ 8km nên độ dài quãng đường về là: \(x+8\) (km)
Vận tốc lúc về lớn hơn lúc đi là 5km/h nên vận tốc lúc về là: \(35+5=40\) (km/h)
Thời gian về là: \(\dfrac{x+8}{40}\) gờ
Do thời gian về ít hơn thời gian đi là 3 phút =1/20 giờ nên ta có pt:
\(\dfrac{x}{35}-\dfrac{x+8}{40}=\dfrac{1}{20}\)
\(\Leftrightarrow x\left(\dfrac{1}{35}-\dfrac{1}{40}\right)=\dfrac{8}{40}+\dfrac{1}{20}\)
\(\Leftrightarrow\dfrac{x}{280}=\dfrac{1}{4}\)
\(\Leftrightarrow x=\dfrac{280}{4}=70\left(km\right)\)

Gọi x là số thứ nhất
⇒ Số thứ hai là: 59 - x
Theo đề bài, ta có phương trình:
2x - 3(59 - x) = -7
2x - 177 + 3x = -7
5x = -7 + 177
5x = 170
x = 170 : 5
x = 34
Vậy số thứ nhất là 34
số thứ hai là 59 - 34 = 25

a) `y=(m-4)x+m` có `a=m-4`
Để là hàm số bậc nhất thì `a≠0`
`=>m-4≠0`
`<=>m≠4`
b) `y=5-3mx` có `a=-3m`
Để là hàm số bậc nhất thì `a≠0`
`=>-3m≠0`
`<=>m≠0`
c) `y=(m-2)x+m` có `a=m-2`
Để là hàm số bậc nhất thì `a≠0`
`=>m-2≠0`
`<=>m≠2`
d) `y=7-5mx` có `a=-5m`
Để là hàm số bậc nhất thì `a≠0`
`=>-5m≠0`
`<=>m≠0`

Lời giải:
Hàm bậc nhất là hàm có dạng $y=ax+b$ với $a,b$ là số thực, $a\neq 0$
Căn cứ vào đó thì:
a. Để $y=(m-4)x+m$ là hsbn thì: $m-4\neq 0$
$\Leftrightarrow m\neq 4$
b.
Để $y=-3mx+5$ là hsbn thì $-3m\neq 0\Leftrightarrow m\neq 0$
c.
Để $y=(m-2)x+m$ là hsbn thì $m-2\neq 0$
$\Leftrightarrow m\neq 2$
d.
Để $y=-5mx+7$ là hsbn thì $-5m\neq 0\Leftrightarrow m\neq 0$



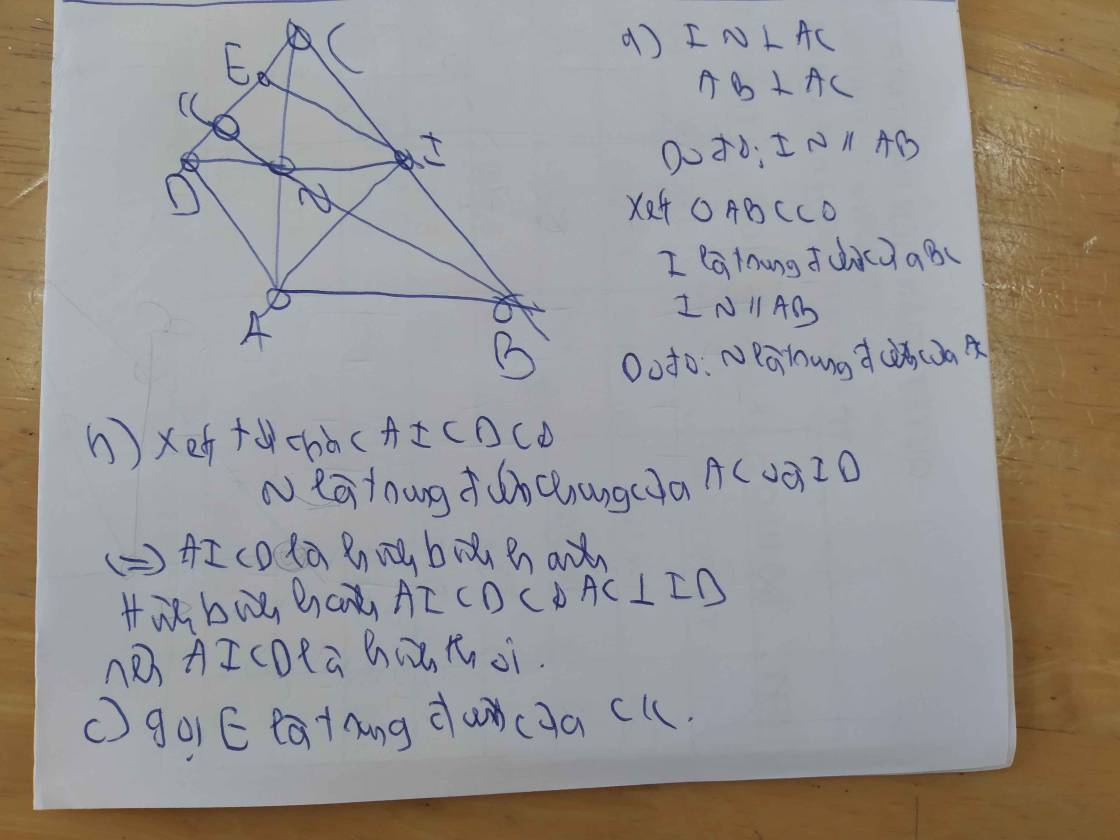

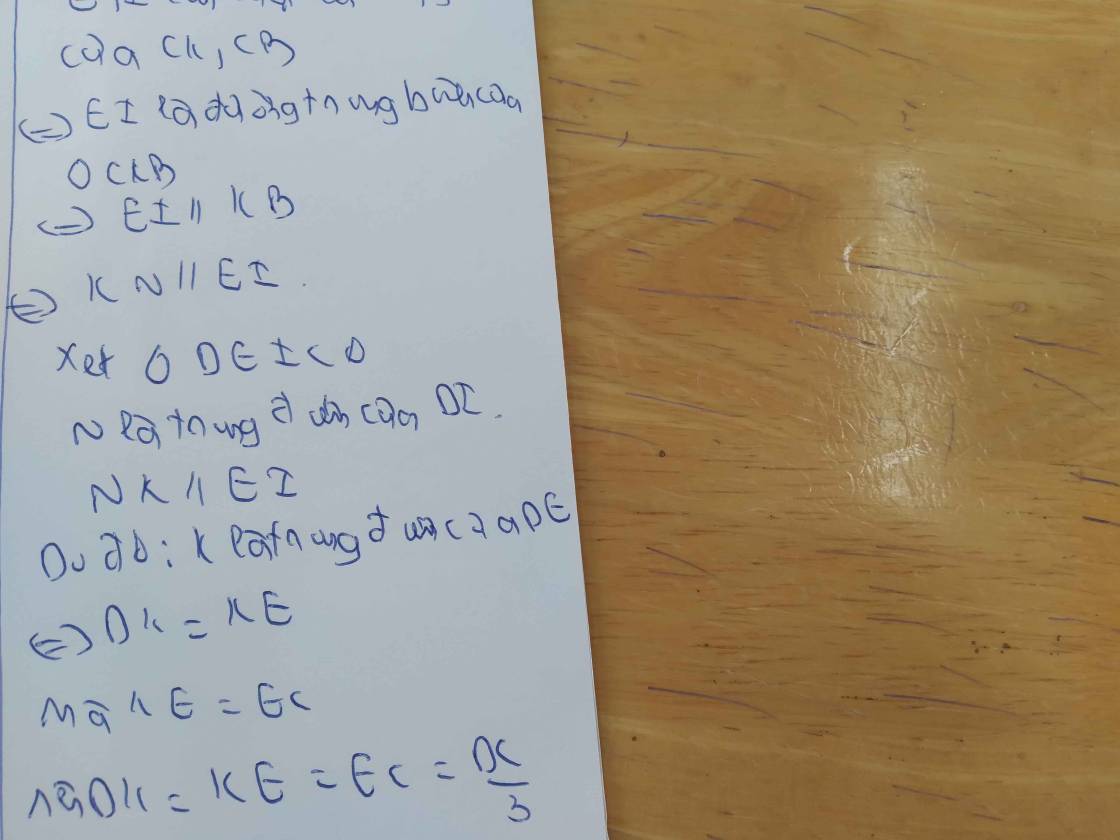


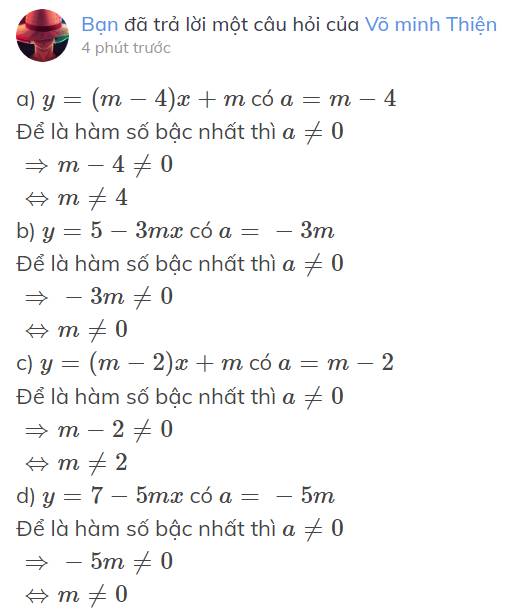

a.
Xét hai tam giác AHB và CAB có:
\(\left\{{}\begin{matrix}\widehat{B}-chung\\\widehat{AHB}=\widehat{CAB}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta AHB\sim\Delta CAB\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{BC}=\dfrac{BH}{AB}\Rightarrow AB^2=BH.BC\)
b.
Do H là trung điểm BM, trong tam giác ABM có AH vừa là đường cao đồng thời là trung tuyến
\(\Rightarrow\Delta ABM\) cân tại A \(\Rightarrow\widehat{ABH}=\widehat{AMH}\)
Mà \(\widehat{AMH}=\widehat{CMK}\) (đối đỉnh)
\(\Rightarrow\widehat{ABH}=\widehat{CMK}\)
Xét hai tam giác ABH và CMK có:
\(\left\{{}\begin{matrix}\widehat{ABH}=\widehat{CMK}\left(cmt\right)\\\widehat{AHB}=\widehat{CKM}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta ABH\sim\Delta CMK\left(g.g\right)\)
c.
Xét hai tam giác AMH và CMK có:
\(\left\{{}\begin{matrix}\widehat{AHM}=\widehat{CKM}=90^0\\\widehat{AMH}=\widehat{CMK}\left(\text{đối đỉnh}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AMH\sim\Delta CMK\left(g.g\right)\Rightarrow\dfrac{AM}{CM}=\dfrac{MH}{MK}\)
\(\Rightarrow\dfrac{AM}{MH}=\dfrac{CM}{MK}\)
Xét hai tam giác AMC và HMK có:
\(\left\{{}\begin{matrix}\dfrac{AM}{MH}=\dfrac{CM}{MK}\left(cmt\right)\\\widehat{AMC}=\widehat{HMK}\left(\text{đối đỉnh}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AMC\sim\Delta HMK\left(c.g.c\right)\)
\(\Rightarrow\dfrac{AM}{MH}=\dfrac{AC}{HK}\Rightarrow MH.AC=AM.HK\)
Mà H là trung điểm BM \(\Rightarrow MH=\dfrac{1}{2}BM\)
\(\Rightarrow\dfrac{1}{2}BM.AC=AM.HK\Rightarrow BM.AC=2AM.HK\)
d.
Từ câu c, do \(\Delta AMC\sim \Delta HMK\Rightarrow \widehat{ACM}=\widehat{HKM}\)
Mà \(\left\{{}\begin{matrix}\widehat{ACM}+\widehat{CAI}=90^0\\\widehat{HKM}+\widehat{HKI}=90^0\end{matrix}\right.\) \(\Rightarrow\widehat{CAI}=\widehat{HKI}\)
Xét hai tam giác CAI và HKI có:
\(\left\{{}\begin{matrix}\widehat{I}-chung\\\widehat{CAI}=\widehat{HKI}\end{matrix}\right.\) \(\Rightarrow\Delta CAI\sim\Delta HKI\left(g.g\right)\)
\(\Rightarrow\dfrac{CI}{HI}=\dfrac{AI}{KI}\Rightarrow KI.CI=HI.AI\)
Ta có:
\(AC^2=AK^2+KC^2=AI^2-IK^2+KC^2\)
\(=AI\left(AH+HI\right)-IK^2+KC^2\)\(=AH.AI+AI.HI-IK^2+KC^2\)
\(=AH.AI+KI.CI-IK^2+KC^2=AH.AI+KI\left(CI-IK\right)+KC^2\)
\(=AH.AI+KI.CK+KC^2=AH.AI+CK.\left(KI+CK\right)\)
\(=AH.AI+CK.CI\) (đpcm)